（第一次学期单元测试）第3章实数—2023-2024学年浙教版七年级数学

试卷更新日期：2023-09-25 类型：单元试卷

进入出卷网下载

一、选择题

1. 25的平方根是（）

A、5 B、－5 C、±5 D、±25

查看试题解析
2. 下列四个实数中，属于无理数的是（）

A、 $\sqrt{4}$ B、 $0 . \overset{\cdot}{3}$ C、-5 D、 $\frac{π}{2}$

查看试题解析
3. 下列计算结果正确的是（）

A、 $\pm \sqrt{4} = 2$ B、 $\sqrt{4} = \pm 2$ C、 $\sqrt{4} = 2$ D、 $\sqrt{(- 4)^{2}} = - 4$

查看试题解析
4. 下列各组数中相等的一组是（）

A、-|2|与 $^{3} \sqrt{- 8}$ B、-4与 $\sqrt{{(- 4)}^{2}}$ C、 $-^{3} \sqrt{2}$ 与 $|^{3} \sqrt{- 2} |$ D、 $\sqrt{2}$ 与 $\frac{1}{\sqrt{2}}$

查看试题解析
5. 有理数a ， b在数轴上的位置如图所示，则下列选项正确的是（）

A、|a|＞|b| B、ab＞0 C、a＋b＞0 D、|a－b|＞1

查看试题解析
6. 下列说法正确的有（）
①无限小数都是无理数；②无理数都是无限小数；③带根号的数都是无理数；④两个无理数的和还是无理数；⑤数轴上的点与实数一一对应.

A、 $2$ 个 B、 $3$ 个 C、 $4$ 个 D、 $5$ 个

查看试题解析
7. 一个长、宽，高分别为50 $cm$ 、8 $cm$ 、20 $cm$ 的长方体铁块锻造成一个立方体铁块，则锻造成的立方体铁块的棱长是（）

A、20 $cm$ B、200 $cm$ C、40 $cm$ D、 $\sqrt{80} cm$

查看试题解析
8. 如图，在数轴上有六个点，且满足AB=BC=CD=DE=EF，则下列各数中与点C表示的数最接近的是（）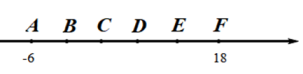

A、-2 B、0 C、2 D、 $2 \sqrt{3}$

查看试题解析
9. 有一个数值转换器，原理如下，则当输人的x为64时，输出的y是（）

A、 $\sqrt{8}$ B、 $\sqrt{18}$ C、 $\sqrt{12}$ D、8

查看试题解析
10. 若a是小于1的正数，则将a， $- a$ ， $- \frac{1}{a}$ ， | $- \frac{1}{a}$ |用“＞”连接起来，正确的是（）

A、 $| - \frac{1}{a} | > a > - a > - \frac{1}{a}$ B、 $| - \frac{1}{a} | > - a > a > - \frac{1}{a}$ C、a＞| $- \frac{1}{a}$ | $＞ - \frac{1}{a} ＞ -$ a D、 $- \frac{1}{a} > a > - a > | - \frac{1}{a} |$

查看试题解析

二、填空题

11. －64的立方根为．

查看试题解析
12. 大于-2小于 $π$ 的所有整数和是.

查看试题解析
13. 下列各数3.1415926，3，1.212222……， $\frac{1}{7}$ ，2-π，-2020中，无理数的个数有个．

查看试题解析
14. 已知一个正数的两个平方根分别是 $x + 5$ 与 $3 x - 17$ ，那么这个正数是．

查看试题解析
15. 按如图所示的程序计算，若输入的a=3，b=4，则输出的结果为．

查看试题解析
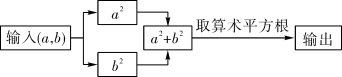16. 下列说法：①任何无理数都是无限不循环小数；②实数与数轴上的点一一对应；③在1和3之间的无理数有且只有 $\sqrt{2} ， \sqrt{3} ， \sqrt{5} ， \sqrt{7}$ 这4个；④近似数1.50所表示的准确数 $x$ 的取值范围是 $1.495 < x < 1.505$ ；⑤a、b互为相反数，则 $\frac{a}{b} = - 1$ ．其中正确的是． (填写序号)

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt[3]{- 8} \times | - 4 |$ ；

(2)、 ${(- 2)}^{3} + 12 \times (1.25 - \frac{1}{6})$ .

查看试题解析
18. 已知2a-1的算术平方根是3，3a+b-1的平方根是±4，c是 $\sqrt{13}$ 的整数部分，求a+2b-c的平方根.

查看试题解析
19. 交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度，所用的经验公式是v=16 $\sqrt{d f}$ ，其中v表示车速(单位：千米/时)，d表示刹车后车轮滑过的距离(单位：米)，f表示摩擦因数．在对某高速公路上发生的一起交通事故的调查中，测得d=30米，f=1.5，肇事汽车的速度是多少？是否超速行驶？ (该高速公路最高时速限制是100千米/时)

查看试题解析
20. 将一个体积为 $125 c m^{3}$ 的立方体体积增加V，而保持立方体的形状不变，则棱长应该增加多少？（用含有V的代数式表示）；若 $V = 875 c m^{3}$ ，则棱长应增加多少厘米？

查看试题解析
21. [阅读材料]
∵ $\sqrt{4}$ ＜ $\sqrt{5}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{5}$ ＜3，

∴1＜ $\sqrt{5}$ -1＜2．

∴ $\sqrt{5}$ -1的整数部分为1．

∴ $\sqrt{5}$ -1的小数部分为 $\sqrt{5}$ -2．

[解决问题]

(1)、填空： $\sqrt{91}$ 的小数部分是．

(2)、已知a是 $\sqrt{21}$ 的整数部分，b是 $\sqrt{21}$ 的小数部分，求代数式（-a）³+（b+4）²的值．

查看试题解析
22. 阅读下面文字，然后回答问题．
给出定义：一个实数的整数部分是不大于这个数的最大数，这个实数的小数部分为这个数与它的整数部分的差的绝对值．例如：2.4的整数部分为2，小数部分为 $2.4 - 2 = 0.4$ ； $\sqrt{2}$ 的整数部分为1，小数部分可用 $\sqrt{2} - 1$ 表示；再如，﹣2.6的整数部分为﹣3，小数部分为 $| - 2.6 - (- 3) | = 0.4$ ．由此我们得到一个真命题：如果 $\sqrt{2} = x + y$ ，其中 $x$ 是整数，且 $0 < y < 1$ ，那么 $x = 1$ ， $y = \sqrt{2} - 1$ ．

(1)、如果 $\sqrt{7} = a + b$ ，其中 $a$ 是整数，且 $0 < b < 1$ ，那么 $a =$ ， $b =$ ；

(2)、如果 $- \sqrt{7} = c + d$ ，其中 $c$ 是整数，且 $0 < d < 1$ ，那么 $c =$ ， $d =$ ；

(3)、已知 $3 + \sqrt{7} = m + n$ ，其中m是整数，且 $0 < n < 1$ ，求 $| m - n |$ 的值；

查看试题解析
23. 在学习《实数》内容时，我们通过“逐步逼近”的方法可以计算出 $\sqrt{2}$ 的近似值，得出1.4＜ $\sqrt{2}$ ＜1.5.利用“逐步逼近“法，请回答下列问题：

(1)、 $\sqrt{19}$ 介于连续的两个整数a和b之间，且a＜b，那么a= ， b=.

(2)、x是 $\sqrt{19}$ +2的小数部分，y是 $\sqrt{19}$ −1的整数部分，则x= ， y=.

(3)、在（2）的条件下，求（ $\sqrt{19}$ −x）^y的平方根.

查看试题解析

（第一次学期单元测试） 第3章 实数—2023-2024学年浙教版七年级数学

一、选择题

二、填空题

三、解答题

（第一次学期单元测试）第3章实数—2023-2024学年浙教版七年级数学