（第一次学期同步） 3.3立方根—2023-2024学年浙教版七年级数学

试卷更新日期：2023-09-24 类型：同步测试

进入出卷网下载

一、选择题

1. $- \frac{1}{27}$ 立方根为（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- \frac{1}{9}$ D、 $\frac{1}{9}$

查看试题解析
2. $^{3} \sqrt{{(- 8)}^{3}}$ 的值是（）

A、-8． B、8 C、±8 D、以上都不对

查看试题解析
3. 下列运算中正确的个数有（）
① $\sqrt{16}$ ＝±4；② $\sqrt[3]{- 8}$ ＝±2；③-2²＝4；④（-1）²⁰²²＝1.

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 若 $-^{3} \sqrt{a} =^{3} \sqrt{\frac{7}{8}}$ ，则a的值是（）

A、 $\frac{7}{8}$ B、- $\frac{7}{8}$ C、± $\frac{7}{8}$ D、 $\frac{343}{512}$

查看试题解析
5. 若 $| x - 8 | + \sqrt{y - 3} = 0 ， \sqrt[y]{x}$ 的值为（）

A、2 B、-2 C、±2 D、4

查看试题解析
6. 若某自然数的立方根为 $a$ ，则它前面与其相邻的自然数的立方根是（）

A、 $a - 1$ B、 $\sqrt[3]{a - 1}$ C、 $\sqrt[3]{a^{3} - 1}$ D、 $a^{3} - 1$

查看试题解析
7. 下列4个说法：①1的立方根是它本身；②数轴上任意一点都对应一个有理数；
③算式5÷6× $\frac{1}{6}$ =5；④对于任意一个实数a，都可以用 $\frac{1}{a}$ 表示它的倒数。
说法正确的是（）

A、①② B、③④ C、① D、②③④

查看试题解析
8. 下列实数，介于5和6之间的是（）

A、 $\sqrt{21}$ B、 $\sqrt{35}$ C、 $\sqrt{42}$ D、 $^{3} \sqrt{64}$

查看试题解析
9. 下列说法： $①$ 任意一个数都有两个平方根；② $\sqrt{3}$ 是3的平方根；③-125的立方根是±5； $④ \frac{\sqrt{3}}{2}$ 是一个分数；⑤负数没有立方根.其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 一张纸的厚度为0.09mm，假设连续对折始终都是可能的，那么至少对折n次后，所得的厚度可以超过厚度为0.9cm的数学课本.则n的值为（）

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

11. $2^{6}$ 的立方根是．

查看试题解析
12. 有一个数值转换器，计算流程如图所示，当输入x的值为8时，输出的值是．

查看试题解析
13. 已知 $\sqrt[3]{2.022} \approx 1.2645$ ， $\sqrt[3]{20.22} \approx 2.7243$ ，则 $\sqrt[3]{- 0.002022} \approx$ ．

查看试题解析
14. 一个正数 $a$ 的两个平方根是 $m + 7$ 和 $2 m - 1$ ，则 $a - m$ 的立方根为.

查看试题解析
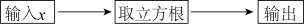15. 一个正方体的体积扩大为原来的27倍，则它的棱长变为原来的倍．

查看试题解析
16. 已知实数a、b、c在数轴上的位置如图所示，化简代数式|a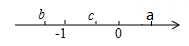|- $\sqrt{(a + c)^{2}}$ + $\sqrt{(c - a)^{2}}$ - $\sqrt[3]{- b^{3}}$ 的结果等于.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{\frac{1}{16}} - \sqrt{36} + \sqrt[3]{8}$ ；

(2)、 $\sqrt{2^{2}} - \sqrt[3]{- 64} + | 1 - \sqrt{2} |$ ．

查看试题解析
18. 已知x是 $- 64$ 的立方根，y的算术平方根是 $\sqrt{13}$ ，求 $x + y$ 的平方根．

查看试题解析
19. 若一个立方体木块的体积是0.125m³ ，现将它锯成8个同样大小的立方体小木块，求每个小立方体木块的表面积．

查看试题解析
20. 已知a的立方根是2，b是 $\sqrt{13}$ 的整数部分，c是9的平方根，求a+b+c的算术平方根.

查看试题解析
21. 已知 $\sqrt[3]{389017}$ 为整数，为计算它的值，请你思考并回答下列问题.

(1)、整数1至9中，立方后，个位数字为7的是；

(2)、 $1 0^{3} = 1000$ ， $10 0^{3} = 1000000$ ，由此可知： $\sqrt[3]{389017}$ 是位数；

(3)、计算 $6 0^{3}$ ， $7 0^{3}$ ， $8 0^{3}$ ，再求 $\sqrt[3]{389017}$ 的值.

查看试题解析
22. 已知某个正数的两个平方根分别是 $a - 12$ 和 $\frac{a + 3}{4}$ ， $b - 8$ 的立方根是2．

(1)、求ab的值．

(2)、求 $a + b$ 的平方根．

查看试题解析
23. 据说，我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是59319，希望求它的立方根．华罗庚脱口而出：39．邻座的乘客十分惊讶，忙问计算的奥秘．你知道华罗庚是怎样迅速准确地计算出来的吗?请按照下面的问题试一试：

(1)、由 $1 0^{3} = 1000$ ， $10 0^{3} = 1000000$ ，可以确定 $\sqrt[3]{59319}$ 是位数，由59319的个位上的数是9，可以确定 $\sqrt[3]{59319}$ 的个位上的数字是，如果划去59319后面的三位319得到数59，而 $3^{3} = 27$ ， $4^{3} = 64$ ，由此可以确定 $\sqrt[3]{59319}$ 的十位上的数字是；

(2)、已知32768，－274625都是整数的立方，按照上述方法，请你分别求它们的立方根．

查看试题解析