江西省南昌市二十八中教育集团2023—2024学年九年级上学期数学开学考试试卷
试卷更新日期:2023-09-22 类型:开学考试
一、选择题(本大题共6小题,每小题3分,共18分)
-
1. 中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米 ,数字“0.000000000142”用科学记数法表示为( )A、 B、 C、 D、3. 若一个三角形的三边长分别为2、6、a , 则a的值可以是( )A、3 B、4 C、7 D、84. 下列二次根式中,能与合并的是( )A、 B、 C、 D、5. 如图,在中,点D , E , F分别是 , , 中点,以这些点为顶点,在图中能画出多少个平行四边形( )
2. 石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米 ,数字“0.000000000142”用科学记数法表示为( )A、 B、 C、 D、3. 若一个三角形的三边长分别为2、6、a , 则a的值可以是( )A、3 B、4 C、7 D、84. 下列二次根式中,能与合并的是( )A、 B、 C、 D、5. 如图,在中,点D , E , F分别是 , , 中点,以这些点为顶点,在图中能画出多少个平行四边形( ) A、1个 B、2个 C、3个 D、4个6. 如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( )
A、1个 B、2个 C、3个 D、4个6. 如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( ) A、
A、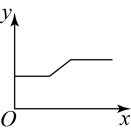 B、
B、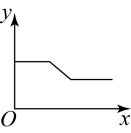 C、
C、 D、
D、
二、填空题(本大题共6小题,每小题3分,共18分)
-
7. 分解因式:.8. 某校举行了“珍爱生命,预防溺水”为主题的演讲比赛,提高学生的安全意识.演讲者的最终比赛成绩按照演讲内容、现场效果、外在形象三项得分分别占40%,40%,20%的比例折算.已知李明同学的三项原始得分分别是90分,95分,90分,那么李明同学最终比赛成绩为分.9. 在平面直角坐标系中,将向下平移3个单位,所得函数图象过 , 则a的值为.10. 以正五边形的顶点C为旋转中心,按顺时针方向旋转,使得新五边形的顶点落在直线上,则正五边形旋转的度数至少为°.
 11. 如图,在中, , , D , E分别是边 , 的中点,点F在上,且 , 则的长是.
11. 如图,在中, , , D , E分别是边 , 的中点,点F在上,且 , 则的长是. 12. 已知函数与 , 若 , 则x的值是.
12. 已知函数与 , 若 , 则x的值是.三、解答题(本大题共5小题,每小题6分,共30分)
-
13. 计算:(1)、(2)、解方程:14. 以下是某同学化简分式的部分运算过程:
解:原式 ……第一步
……第二步
……第三步
(1)、上面的运算过程中第步开始出现了错误;(2)、请你写出完整的解答过程.15. 如图,等边三角形的边长是4,D , E分别为边 , 的中点,延长至点F , 使 , 连接 , , . (1)、求证:四边形是平行四边形;(2)、求的长.16. 已知四边形是平行四边形,为对角线,分别在图①、图②中按要求作图(保留作图痕迹,不写做法).
(1)、求证:四边形是平行四边形;(2)、求的长.16. 已知四边形是平行四边形,为对角线,分别在图①、图②中按要求作图(保留作图痕迹,不写做法).

图① 图②
(1)、如图①,点P为上任意一点,请仅用无刻度的直尺在上找出另一点Q , 使;(2)、如图②,点P为上任意一点,请仅用无刻度的直尺在上找出一点Q , 使.17. 已知关于x的一元二次方程 , 其中a , b , c分别为三边的长.(1)、如果是方程的一个根,试判断的形状,并说明理由;(2)、如果是等边三角形,试求这个一元二次方程的根.四、解答题(本大题共3小题,每小题8分,共24分)
-
18. “人间烟火味,最抚凡人心”,地摊经济、小店经济是就业岗位的重要来源.某经营者购进了型和型两种玩具,已知用520元购进型玩具的数量比用175元购进型玩具的数量多30个,且型玩具单价是型玩具单价的倍.(1)、求两种型号玩具的单价各是多少元?
根据题意,甲、乙两名同学分别列出如下方程:
甲: , 解得 , 经检验是原方程的解.
乙: , 解得 , 经检验是原方程的解.
则甲所列方程中的表示 , 乙所列方程中的表示;
(2)、该经营者准备用1350元以原单价再次购进这两种型号的玩具共200个,则最多可购进型玩具多少个?19. 已知一次函数(k、b为常数,且)的图象(如图1).
图1 图2
(1)、求k , b的值;(2)、正比例函数(m为常数,)与一次函数相交于点P(如图2),则不等式的解集为;不等式组的解集为.20. 古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:如果一个三角形的三边长分别为a、b、c , 设 , 则三角形的面积.我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):如果一个三角形的三边长分别为a、b、c , 则三角形的面积.依据上述公式解决下列问题:(1)、若一个三角形的三边长分别是5,6,7,则这个三角形的面积等于;(2)、若一个三角形的三边长分别是 , 3, , 求这个三角形的面积.五、解答题(本大题共2小题,每小题9分,共18分)
-
21. 甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:根据以上信息,整理分析数据如下:

平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)、 , , .(2)、填空:(填“甲”或“乙”).从中位数的角度来比较,成绩较好的是;从众数的角度来比较,成绩较好的是;成绩相对较稳定的是.
(3)、从甲、乙两名队员中选一名队员参加比赛,选谁更合适,为什么?22. 已知:直线与x轴、y轴分别相交于点A和点B , 点C在线段上.将沿折叠后,点O恰好落在边上点D处. (1)、直接写出点A , 点B的坐标;(2)、求的长度;(3)、取的中点M , 若点P在y轴上,点Q在直线上,存在以C、M、P、Q为顶点的四边形为平行四边形,则点Q的坐标为.
(1)、直接写出点A , 点B的坐标;(2)、求的长度;(3)、取的中点M , 若点P在y轴上,点Q在直线上,存在以C、M、P、Q为顶点的四边形为平行四边形,则点Q的坐标为.六、(本大题共1题,共12分)
-
23. 我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
某校数学兴趣小组,在学习完勾股定理和实数后,进行了如下的问题探索与分析:
【提出问题】已知 , 求的最小值
【分析问题】由勾股定理,可以通过构造直角三角形的方法,来分别表示长度为和的线段,将代数求和转化为线段求和问题.
【解决问题】
 (1)、如图,我们可以构造边长为1的正方形 , P为边上的动点.设 , 则.则线段线段;(2)、在(1)的条件下,已知 , 求的最小值;(3)、【应用拓展】应用数形结合思想,求的最大值.
(1)、如图,我们可以构造边长为1的正方形 , P为边上的动点.设 , 则.则线段线段;(2)、在(1)的条件下,已知 , 求的最小值;(3)、【应用拓展】应用数形结合思想,求的最大值.