江西省南昌市师大附中滨江校区2023-2024学年九年级上学期开学考试试卷-在线组卷题库

1. 下列各数，最小的是（）

A、0 B、0.1 C、 $- 4$ D、 $- π$

查看试题解析
2. 下列运算正确的是（）

A、 ${(x^{2})}^{3} = x^{6}$ B、 $7 a^{2} - 5 a^{2} = 2$ C、 $x^{- 2} = - x^{2}$ D、 $3 x + 2 y = 5 x y$

查看试题解析
3. 如图，点A在数轴上表示的数是3，过点A作直线l垂直于OA ，在l上取点B ，使 $A B = 2$ ，以原点O为圆心，以OB为半径作弧，弧与数轴的交点C表示的数为（）

A、 $\sqrt{5}$ B、 $\sqrt{6}$ C、 $\sqrt{10}$ D、 $\sqrt{13}$

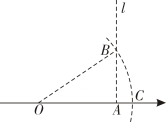查看试题解析
4. 下面统计调查中，适合采用全面调查的是（）

A、调查市场上某食品防腐剂是否符合国家标准 B、对某品牌手机的防水性能的调查 C、疫情期间对国外入境人员的核酸检测 D、调查我市初中生每周“诵读经典”的时间

查看试题解析
5. 如图，在平行四边形ABCD中，E、F是对角线BD上的两点，若要使四边形AECF为平行四边形，则以下三种方案中正确的方案是（）
甲：只需要满足 $B F = D E$ ；乙：只需要满足 $A E = C F$ ；丙：只需要满足 $A E ∥ C F$ ，

A、甲、乙 B、甲、丙 C、乙、丙 D、甲、乙、丙

查看试题解析
6. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 的图象经过正方形OABC的顶点A和C ，已知点A的坐标为 $(1 ， - 2)$ ，则k的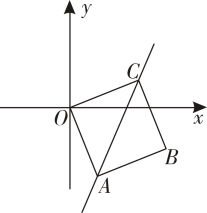值为（）

A、1 B、2 C、3 D、4

查看试题解析

7. 分解因式： $m x^{2} - m y^{2} =$ ．

查看试题解析
8. 已知点 $A (2 ， 5) ， B (4 ， 5)$ 是抛物线 $y = 2 x^{2} + b x + c$ 上的两点，则这条抛物线的对称轴为直线．

查看试题解析
9. 如图，在平面直角坐标系中，函数 $y = 2 x$ 与 $y = k x + b (k < 0)$ 的图象交于点 $P (m ， 2)$ ，则不等式 $k x + b > 2 x$ 的解集为．

查看试题解析
10. 师大附中今年春季开展体操活动，小明收集、整理了成绩突出的甲、乙两队队员（各50名）的身高情况，得到以下信息：平均身高（单位：cm）分别为： ${\bar{x}}_{甲} = 160 ， {\bar{x}}_{乙} = 162$ ；方差分别为： $S_{甲}^{2} = 1.5 ， S_{乙}^{2} = 2.6$ ．现要从甲、乙两队中选出身高比较整齐的一个队参加上一级的体操比赛，根据上述数据，应该选择．（填写“甲”或“乙”）

查看试题解析
11. 淄博烧烤风靡全国．某烧烤店今年5月份的盈利额为20万元，预计7月份的盈利额将达28.8万元，设每月增长的百分率相同，则6月份的盈利额为万元．

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 2 \sqrt{3}$ ，点 $E$ 是 $B C$ 的中点，点 $P$ 是 $A B$ 边上一动点，将 $△ B P E$ 沿 $P E$ 折叠，点 $B$ 的对应点为点 $B^{'}$ ，当射线 $E B^{'}$ 经过矩形 $A B C D$ 一边的中点时（不含点 $E$ ），则 $B P$ 的长为．

查看试题解析

13. 解方程：

(1)、 $x (x - 4) + x - 4 = 0$ ；

(2)、 $x^{2} - 1 = 4 x$ ．

查看试题解析
14.

(1)、计算： $\sqrt{9} - (- 2)^{3} + \sqrt[3]{- 8}$ ；

(2)、解不等式组： ${\begin{array}{l} 1 - \frac{x + 1}{3} \geq 0 \\ 3 + 4 (x - 1) > 1 \end{array}$

查看试题解析
15. 先化简，再求值： $(1 - \frac{1}{a}) \div \frac{a^{2} - 1}{a}$ ，其中 $a = - 2$ ．

查看试题解析
16. 如图，直线 $l_{1} ： y = x + 3$ 与直线 $l_{2} ： y = - 2 x + b$ 交于点 $C (1 ， m)$ ．

(1)、求m、b的值；

(2)、 $P (a ， 0)$ 为x轴上一个动点，过P作x轴的垂线，分别交直线 $l_{1} ， l_{2}$ 于点E ， F ．若 $E F = 3$ ，求a值．

查看试题解析
17.
我们把能二等分多边形面积的直线称为多边形的“好线”，请用无刻度的直尺作出图（1）、图（2）的“好线”．其中图（1）是一个平行四边形，图（2）由一个平行四边形和一个正方形组成．（保留作图痕迹，不写作法）

查看试题解析

18. 已知关于x的一元二次方程 $x^{2} + (2 k + 1) x + k^{2} - 1 = 0$ 有实数根．

(1)、求实数k的取值范围．

(2)、设方程的两个实数根分别为 $x_{1} ， x_{2}$ ，若 $x_{1}^{2} + x_{2}^{2} = 9$ ，求k的值．

查看试题解析
19. 为弘扬红色文化，传颂红色故事，某学校特在九年级开展了红色文化知识竞赛活动，并随机抽取了20名参赛选手的成绩（竞赛成绩均为正数，满分100分）进行统计分析．随机抽取的成绩如下：77，86，80，76，70，100，95，80，75，90，94，86，68，95，88，78，90，82，86，100，整理数据：
分数
          $60 < x \leq 70$
          $70 < x \leq 80$
          $80 < x \leq 90$
          $90 < x \leq 100$
人数
2
a
b
5
根据以上信息回答下列问题：

(1)、填空： $a =$ ， $b =$ ．

(2)、这20名参赛人员成绩的众数为，中位数为；

(3)、小李的参赛成绩为87分，你认为他的成绩属于“中上”水平吗？请说明理由；

(4)、该学校九年级共有460名学生参加了竞赛，若成绩在90分（包含90分）以上为优秀，请你估计此次知识竞赛中优秀的人数．

查看试题解析

20. 二次函数

y = a x^{2} + b x + c

．图象上部分点的横坐标x ，纵坐标y的对应值如表：

x	…	$- 5$	$- 4$	$- 3$	$- 2$	$- 1$	0	1	2	m	…
y	…	$- 19$	$- 12$	$- 7$	$- 4$	$- 3$	$- 4$	$- 7$	n	$- 19$	…

(1)、这个二次函数的表达式为，顶点坐标是；

(2)、表中的

m =

，

n =

；

(3)、若

P (x_{1} ， y_{2}) ， Q (x_{2} ， y_{2})

是这个函数图象上的两点，且

x_{1} < x_{2} < - 1

，则

y_{1}

y_{2}

（填“>”或“=”或“<”）：

(4)、当

a \geq x \geq a + 1

时，二次函数的最大值为

- 5

，求实数a的值．

查看试题解析

21. 有一块长为a米，宽为b米的长方形场地，计划在该场地上修建宽均为x米的两条互相垂直的道路，余下的四块长方形场地建成草坪．

(1)、已知 $a = 24 ， b = 14$ ，且四块草坪的面积和为264平方米，则每条道路的宽x为多少米？

(2)、若 $a ： b = 2 ： 1 ， x = 2$ ，且四块草坪的面积和为264平方米，则原来矩形场地的长和宽各为多少米？

(3)、已知 $a = 28 ， b = 14$ ，现要在场地上修建若干条宽均为2米的纵横小路，假设有m条水平方向的小路，n条竖直方向的小路（其中 $m > 2$ ， m ， n为常数），使草坪地的总面积为132平方米，则 $m^{2} + n^{2} =$ （直接写出答案）．

查看试题解析
22. 综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．
操作一：对折正方形纸片ABCD ，使AD与BC重合，得到折痕EF ，把纸片展平；
操作二：在AD上选一点P ，沿BP折叠，使点A落在正方形内部点M处，把纸片展平，连接PM ， BM ，并延长PM交CD于点Q ，连接BQ ．

(1)、初步感知
如图1，当点M在EF上时，线段CQ与MQ的数量关系为； $∠ P B Q =$ 度．

(2)、迁移探究
改变点P在AD上的位置（点P不与点A ， D重合），如图2，请判断线段CQ与MQ的数量关系及 $∠ P B Q$ 的度数，并说明理由；

(3)、拓展应用
已知正方形纸片ABCD的边长为10，在以上探究中，当 $F Q = 3$ 时，直接写出AP的长．

查看试题解析

23. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴交于A ， B两点（A在B的左侧），与y轴交于点N ，过A点的直线： $l ： y = - x - 1$ 与y轴交于点C ，与抛物线 $y = - x^{2} + b x + c$ 的另一个交点为 $D (5 ， - 6)$ ，已知P点为抛物线 $y = - x^{2} + b x + c$ 上一动．点（不与A、D重合）．

(1)、求抛物线的解析式；

(2)、当点P在直线l上方的抛物线上时，过P点作 $P E ∥ x$ 轴交直线l于点E ，作 $P F ∥ y$ 轴交直线l于点F ，求 $P E + P F$ 的最大值；

(3)、设M为直线l上的动点，以NC为一边且顶点为N ， C ， M ， P的四边形是平行四边形，直接写出所有符合条件的M点坐标．

查看试题解析

江西省南昌市师大附中滨江校区2023-2024学年九年级上学期开学考试试卷

一、选择题（共6小题，每小题3分，共18分）

二、填空题（共6小题，每小题3分，共18分）

三、解答题（共5小题，每小题6分，共30分）

四、解答题（共3小题，每小题8分，共24分）

五、解答题（共2小题，每小题9分，共18分）

六、解答题（共1小题，共12分）

分数	$60 < x \leq 70$	$70 < x \leq 80$	$80 < x \leq 90$	$90 < x \leq 100$
人数	2	a	b	5