重庆市重点学校2023年中考三模数学考试试卷
试卷更新日期:2023-09-22 类型:中考模拟
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的相反数是( )A、 B、 C、 D、2. 如图所示是一个钢块零件,它的左视图是( )
 A、
A、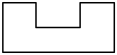 B、
B、 C、
C、 D、
D、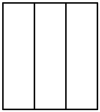 3. 如图,在平面直角坐标系中,与是以原点为位似中心的位似图形,若:: , 的面积为 , 则的面积为( )
3. 如图,在平面直角坐标系中,与是以原点为位似中心的位似图形,若:: , 的面积为 , 则的面积为( ) A、 B、 C、 D、4. 如图, , 含的直角三角板的直角顶点在直线上,若 , 则的度数为( )
A、 B、 C、 D、4. 如图, , 含的直角三角板的直角顶点在直线上,若 , 则的度数为( ) A、
A、
B、
C、
D、5. 若一个正方形的面积是 , 则它的边长最接近的整数是( )A、 B、 C、 D、6. 在“双减政策”的推动下,实外初三学生课后作业时长明显减少年上学期每天作业平均时长为 , 经过年下学期和年上学期两次调整后,年上学期平均每天作业时长为设这两学期该校平均每天作业时长每期的下降率为 , 则可列方程为( )A、 B、
C、 D、7. 观察下列一组图形,其中图形中共有颗黑点,图形中共有颗黑点,图形中共有颗黑点,按此规律,图形中黑点的颗数是( )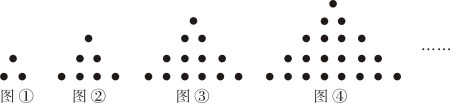 A、 B、 C、 D、8. 如图,已知的半径为 , 为的弦, , 点在上,且满足 , 交于点 , 则的长为( )
A、 B、 C、 D、8. 如图,已知的半径为 , 为的弦, , 点在上,且满足 , 交于点 , 则的长为( ) A、
A、
B、
C、
D、9. 如图,正方形的边长为 , 点为边上一点, , 点为边上一动点,连接、交于点 , 连接 , 当时,则的长为( )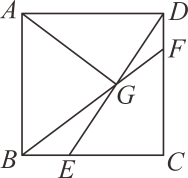 A、 B、 C、 D、10. 已知三个函数: , , , 下列说法:
A、 B、 C、 D、10. 已知三个函数: , , , 下列说法:
当时,的值为或;
对于任意的实数 , , 若 , , 则;
若时,则;
若当式子中的取值为与时,的值相等,则的最大值为 .
以上说法中正确的个数是( )A、 B、 C、 D、二、填空题(本大题共8小题,共32.0分)
-
11. 计算: .12. 一个多边形的内角和与外角和的差为 , 则它的边数为 .13. 如图,在中, , 是的垂直平分线,分别交 , 于点D,E.若 , 则的度数为 .
 14. 现有分别标有汉字“决”“胜”“中”“考”的四张卡片,它们除汉字外完全相同,若把四张卡片背面朝上,洗匀后放在桌面上,然后随机抽出一张,不放回,再随机抽出一张,两次抽出的卡片上的汉字能组成“决”“胜”的概率是 .15. 如图,在矩形中, , , 以点为圆心,的长为半径画弧,与、分别交于点、 , 则图中阴影部分的面积为 结果保留
14. 现有分别标有汉字“决”“胜”“中”“考”的四张卡片,它们除汉字外完全相同,若把四张卡片背面朝上,洗匀后放在桌面上,然后随机抽出一张,不放回,再随机抽出一张,两次抽出的卡片上的汉字能组成“决”“胜”的概率是 .15. 如图,在矩形中, , , 以点为圆心,的长为半径画弧,与、分别交于点、 , 则图中阴影部分的面积为 结果保留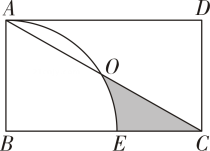 16. 如图,在平面直角坐标系中,点在第一象限,连接 , 过点作轴于点 , 反比例函数的图象分别与、交于点、 , 连接 , 若为的中点,且四边形的面积为 , 则的值为 .
16. 如图,在平面直角坐标系中,点在第一象限,连接 , 过点作轴于点 , 反比例函数的图象分别与、交于点、 , 连接 , 若为的中点,且四边形的面积为 , 则的值为 .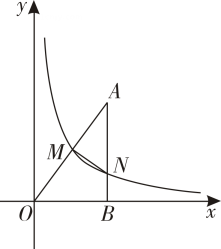 17. 关于的不等式组的解集为 , 且关于的分式方程有非负整数解,则所有满足条件的整数的和为 .18. 一个四位数 , 若千位上的数字与百位上的数字之和与十位上的数字与个位上的数字之和的积等于 , 则称这个四位数为“六秩数”,例如,对于四位数 , , 为“六秩数”若 , , 记 , 则 ;若是一个“六秩数”,且是一个完全平方数,记 , 则的最大值与最小值的差为 .
17. 关于的不等式组的解集为 , 且关于的分式方程有非负整数解,则所有满足条件的整数的和为 .18. 一个四位数 , 若千位上的数字与百位上的数字之和与十位上的数字与个位上的数字之和的积等于 , 则称这个四位数为“六秩数”,例如,对于四位数 , , 为“六秩数”若 , , 记 , 则 ;若是一个“六秩数”,且是一个完全平方数,记 , 则的最大值与最小值的差为 .三、解答题(本大题共8小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算:
(1)、;
(2)、 .20. 如图,在菱形中,对角线、相交于点 .
 (1)、尺规作图:在的延长线上截取 , 连接 , 再过点作的垂线交于点保留作图痕迹,不写作法;(2)、求证:四边形为矩形.
(1)、尺规作图:在的延长线上截取 , 连接 , 再过点作的垂线交于点保留作图痕迹,不写作法;(2)、求证:四边形为矩形.
证明: ,
▲ ,
四边形是菱形,
, , ,
,
,
▲ ,
又 ,
四边形为平行四边形,
▲ ,
,
▲ ,
,
四边形为矩形.21. 为了更好地关爱学生的用眼健康,某校开展了“健康用眼”知识答题竞赛现从该校七、八年级中各随机抽取名学生的竞赛成绩百分制进行整理、描述和分析成绩得分用表示,共分成四组: , , , , 下面给出了部分信息:
七年级名学生的竞赛成绩是: , , , , , , , , , .
八年级名学生的竞赛成绩在组中的数据是: , , .
七、八年级抽取的学生竞赛成绩统计表:年级
平均数
中位数
众数
七年级
八年级
根据以上信息,解答下列问题:
(1)、填空: , , ;(2)、根据以上数据,你认为该校七、八年级中哪个年级学生掌握用眼健康知识较好?请说明理由一条理由即可;(3)、该校七年级人、八年级人参加了此次答题竞赛活动,请估计两个年级参加竞赛活动的成绩不低于分的共有多少人?22. 五一假期,不少人选择乘坐飞机出游妈妈和小明从航站楼入口点处前往登机口点处登机已知点位于点东北方向且米点的正东方向有另一入口点 , 商店位于点的正北方向,同时位于点的南偏东 , 米.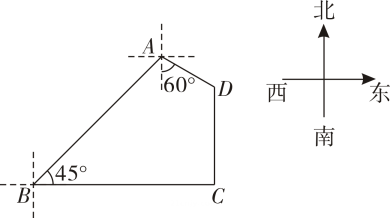 (1)、求两个入口的距离;结果保留根号
(1)、求两个入口的距离;结果保留根号
(2)、妈妈和小明到达航站楼时间为上午: , 登机时间为:妈妈见时间尚早,决定和小明一起先去商店处逛逛,他们沿路线行走,步行速度为米分,在商店处逗留分钟,请计算说明妈妈和小明是否能准时登机?参考数据: ,23. 某新修公路沿线需要进行绿化施工,由甲、乙两工程队合作完成已知若由甲工程队单独施工,需要天才能完成此项工程;若由乙工程队先施工天,剩下的由甲、乙合作施工,则还需天才能完成此项工程.(1)、求乙工程队单独完成此项工程需要多少天?(2)、若甲工程队每天所需费用为万元,乙工程队每天所需费用为万元甲、乙两工程队合作完成此项工程,总费用恰为万元,则应安排甲工程队施工多少天?24.
如图,在等腰中, , , 为中点,动点从点出发,沿着方向运动至点处停止连接、 , 设点的运动路程为 , 的面积为 .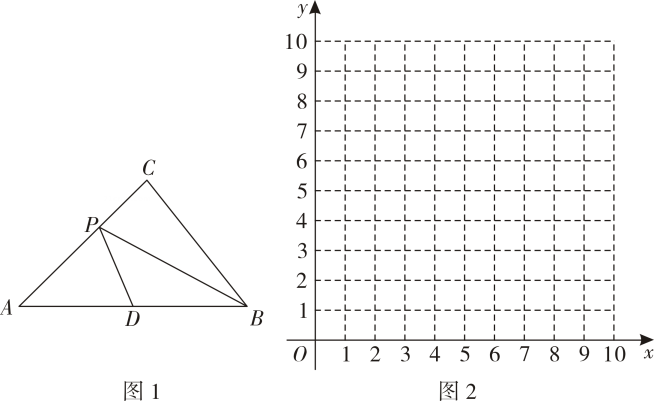 (1)、直接写出与的函数表达式,并写出自变量的取值范围;(2)、请在图中画出函数的图象,并写出该函数的一条性质: ;(3)、已知函数 , 当时,请直接写出自变量的取值范围.25. 如图,在平面直角坐标系中,抛物线与轴交于、两点点在点的左侧 , 与轴交于点 , 连接、 .
(1)、直接写出与的函数表达式,并写出自变量的取值范围;(2)、请在图中画出函数的图象,并写出该函数的一条性质: ;(3)、已知函数 , 当时,请直接写出自变量的取值范围.25. 如图,在平面直角坐标系中,抛物线与轴交于、两点点在点的左侧 , 与轴交于点 , 连接、 .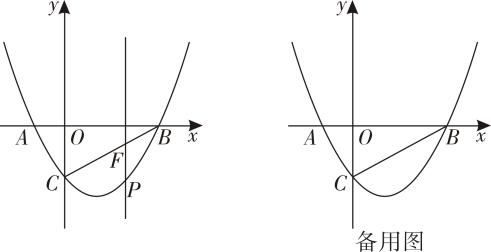 (1)、求的面积;(2)、点为直线下方抛物线上的一动点,过点作轴交直线点 , 求的最大值及此时点的坐标;(3)、将原抛物线沿射线方向平移个单位长度,得到新抛物线 , 新抛物线与轴交于点 , 点为新抛物线对称轴上一动点,点为新抛物线上一动点,当以、、、为顶点的四边形的对角线互相平分时,请直接写出此时点的纵坐标.
(1)、求的面积;(2)、点为直线下方抛物线上的一动点,过点作轴交直线点 , 求的最大值及此时点的坐标;(3)、将原抛物线沿射线方向平移个单位长度,得到新抛物线 , 新抛物线与轴交于点 , 点为新抛物线对称轴上一动点,点为新抛物线上一动点,当以、、、为顶点的四边形的对角线互相平分时,请直接写出此时点的纵坐标.
26. 如图,在等腰中, , AB=BC,点D在线段BC的中垂线上,连接BD、CD.
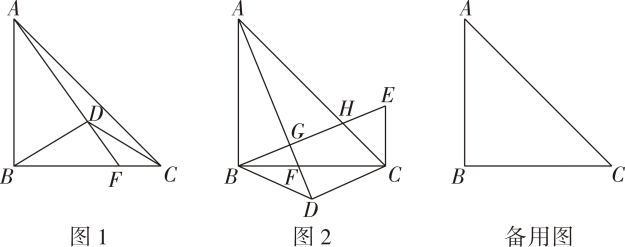 (1)、如图1,若时,连接AD并延长交BC于点F,若AB=6,求的面积;(2)、如图 , 连接 , 若 , 过点作于点 , 交于点 , 过点作交的延长线于点求证:;(3)、在等腰内部有一点 , 连接、、 , 将沿直线翻折至所在平面内得到 , 连接 , 当取得最小值时,请直接写出的值.
(1)、如图1,若时,连接AD并延长交BC于点F,若AB=6,求的面积;(2)、如图 , 连接 , 若 , 过点作于点 , 交于点 , 过点作交的延长线于点求证:;(3)、在等腰内部有一点 , 连接、、 , 将沿直线翻折至所在平面内得到 , 连接 , 当取得最小值时,请直接写出的值.