吉林省松原市前郭县城镇三校2023年中考数学四模考试试卷
试卷更新日期:2023-09-22 类型:中考模拟
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在 , , , 四个数中,最小的数是( )A、 B、 C、 D、2. 年月日下午,“天宫课堂“第二课在中国空间站开讲,由神舟十三号乘组三位航天员翟志刚、王亚平,叶光富进行授课央视新闻抖音号进行全程直播,某一时刻观看人数达到数字用科学记数法可以表示为( )A、 B、 C、 D、3. 不等式的解集在数轴上表示正确的是( )A、
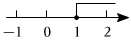 B、
B、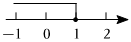 C、
C、 D、
D、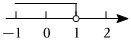 4. 将一副三角板按如图所示放置,则的度数为( )
4. 将一副三角板按如图所示放置,则的度数为( ) A、 B、 C、 D、5. 如图,与相切于点 , 与相交于点 , 若 , , 则的半径为( )
A、 B、 C、 D、5. 如图,与相切于点 , 与相交于点 , 若 , , 则的半径为( ) A、 B、 C、 D、6. 我国古代著作四元玉鉴记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为文.如果每株椽的运费是文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问文能买多少株椽?设这批椽的数量为株,则符合题意的方程是( )A、 B、 C、 D、
A、 B、 C、 D、6. 我国古代著作四元玉鉴记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为文.如果每株椽的运费是文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问文能买多少株椽?设这批椽的数量为株,则符合题意的方程是( )A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
7. 若在实数范围内有意义,则x的取值范围是 .8. 已知 , , 则值为 .9. 标价为元的商品,若打折出售,则售价为 元用含有的代数式表示10. 若关于x的一元二次方程x2+x+m=0有两个相等的实数根,则m= .11. 如图,利用三角支架可以固定平板电脑的位置,这样做的数学道理是 .
 12. 如图 , 将一张矩形纸片对折,使点与点重合,点与点重合,折痕为如图 , 把矩形纸片展平后,沿过点的直线折叠,使点的对应点落在上,折痕为 , 则的度数是
12. 如图 , 将一张矩形纸片对折,使点与点重合,点与点重合,折痕为如图 , 把矩形纸片展平后,沿过点的直线折叠,使点的对应点落在上,折痕为 , 则的度数是 13. 如图,在中, , , 分别以点 , 为圆心大于长度为半径画弧,两弧交于点 , 作射线交于点 , 再以点为圆心,长度为半径画弧,交于点 , 则阴影部分的面积为 .
13. 如图,在中, , , 分别以点 , 为圆心大于长度为半径画弧,两弧交于点 , 作射线交于点 , 再以点为圆心,长度为半径画弧,交于点 , 则阴影部分的面积为 . 14. 如图是由边长为的小正方形组成的的网格,每个小正方形的顶点叫做格点点、、、均在格点上,在网格中将点按下列步骤移动:
14. 如图是由边长为的小正方形组成的的网格,每个小正方形的顶点叫做格点点、、、均在格点上,在网格中将点按下列步骤移动:
第一步:点绕点顺时针旋转得到点;
第一步:点绕点顺时针旋转得到点;
第三步:点绕点逆时针旋转回到点 .
则点经过的路径长为 .
三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 先化简,再求值: , 其中 , .16. 如图,点 , , , 在一条直线上, , , 求证:≌ .
 17. 为了增强学生体质,九年一班决定购进两种体育器材:跳绳和毽子,如果购进根跳绳和个毽子共需元,购进根跳绳和个毽子共需元,求一根跳绳和一个毽子的售价分别是多少元.18. 从一副普通的扑克牌中取出四张牌,它们的牌而数字分别为 , , , 将这四张扑克牌背朝上,洗匀从中随机抽取一张不放回,再从剩余的三张牌中随机抽取一张请利用画树状图或列表的方法,求抽取的这两张牌的牌面数字和为奇数的概率.
17. 为了增强学生体质,九年一班决定购进两种体育器材:跳绳和毽子,如果购进根跳绳和个毽子共需元,购进根跳绳和个毽子共需元,求一根跳绳和一个毽子的售价分别是多少元.18. 从一副普通的扑克牌中取出四张牌,它们的牌而数字分别为 , , , 将这四张扑克牌背朝上,洗匀从中随机抽取一张不放回,再从剩余的三张牌中随机抽取一张请利用画树状图或列表的方法,求抽取的这两张牌的牌面数字和为奇数的概率. 19. 如图,在正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为点、都在格点上,按下列要求作图,使得所画图形的顶点均在格点上.
19. 如图,在正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为点、都在格点上,按下列要求作图,使得所画图形的顶点均在格点上. (1)、在图中以线段为边画一个等腰三角形;(2)、在图中以线段为边画一个轴对称的四边形;(3)、在图中以线段为边画一个中心对称的四边形 , 使其面积为 .20. 为提高学生识骗、防骗能力,谨防上当受骗,学校随机抽查了部分学生进行防诈骗安全知识测试将测试结果分为优,良,及格,不及格四类,并绘制成如图不完整的统计图表.
(1)、在图中以线段为边画一个等腰三角形;(2)、在图中以线段为边画一个轴对称的四边形;(3)、在图中以线段为边画一个中心对称的四边形 , 使其面积为 .20. 为提高学生识骗、防骗能力,谨防上当受骗,学校随机抽查了部分学生进行防诈骗安全知识测试将测试结果分为优,良,及格,不及格四类,并绘制成如图不完整的统计图表.等级
频数人数
频率
优
良
及格
不及格
请你根据统计图表提供的信息解答下列问题:
 (1)、上表中的 , , ;
(1)、上表中的 , , ;
(2)、本次调查共抽取了多少名学生?请补全条形图;
(3)、如果测试结果为不及格的同学应加强防诈骗安全学习,根据调查结果估计该校学生中应加强防诈骗安全学习的学生人数.21. 某人乘车从地去地如图所示,地在地的正北方向,且距离地 , 但 , 两地之间道路维修无法通过按导航指示,车辆沿正西方向行驶至地,再沿北偏东方向行驶到达地,求车辆绕行之后比沿段多行驶多少千米结果精确到参考数据 , ,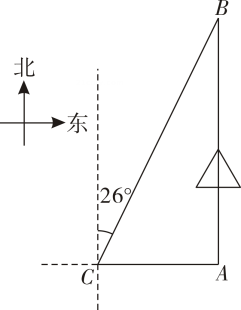 22. 如图,一次函数与反比例函数的图象在第一象限交于和两点,与轴交于点 .
22. 如图,一次函数与反比例函数的图象在第一象限交于和两点,与轴交于点 .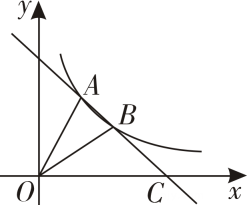 (1)、求反比例函数和一次函数的解析式;
(1)、求反比例函数和一次函数的解析式;
(2)、连接 , , 求的面积.23. 为支援甲地抗击新冠疫情,乙地先后向甲地捐赠两批物资甲、乙两地之间有一条长为的公路从乙地匀速开往甲地,车出发两小时后,车从乙地匀速开往甲地两车同时到达甲地,车行驶路程与车行驶路程的差单位:与车行驶时间单位:之间的函数关系如图所示. (1)、车的速度为 , 车的速度为 , ;
(1)、车的速度为 , 车的速度为 , ;
(2)、求车行驶过程中关于的函数解析式,并写出的取值范围;
(3)、当、两车之间的距离为时,直接写出的值.24. 已知正方形边长为 , 对角线 , 相交于点 , 过点作射线 , , 分别交 , 于点 , , 且 . (1)、如图 , 当时,求证:四边形是正方形;
(1)、如图 , 当时,求证:四边形是正方形;
(2)、如图 , 将射线 , 绕着点进行旋转.
在旋转过程中,判断线段与的数量关系,并给出证明;
四边形的面积为 ;
(3)、如图 , 在四边形中, , , 连接若 , 请直接写出四边形的面积.
25. 如图,在矩形中, , 连接 , , 点从点出发,以每秒个单位长度的速度沿线段向终点运动;同时点从点出发,以每秒个单位长度的速度沿折线向终点运动,以 , 为邻边作平行四边形设运动时间为秒,平行四边形和矩形重叠部分的图形面积为 .
 (1)、当点在上时, ;
(1)、当点在上时, ;
(2)、求关于的函数解析式,并写出的取值范围;
(3)、连接 , 直接写出当时的值.26. 在平面直角坐标系中,抛物线的顶点为 , 与轴相交于点 .(1)、点的坐标为 ,点的坐标为 用含的式子表示;
(2)、设抛物线的函数图象最高点的纵坐标为:
当时, ;当时, ;
写出关于的函数解析式及自变量的取值范围;
(3)、将抛物线的函数图象记为图象 , 将抛物线的函数图象记为图象 , 图象和图象组合成的图象记为图象 , 点在轴上且纵坐标为 , 过点作直线轴于点请直接写出直线与图象有三个交点时的取值范围.