吉林省白山八中、九中2023年中考五模数学考试试卷试卷
试卷更新日期:2023-09-22 类型:中考模拟
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 不等式的解集在数轴上表示正确的是( )A、
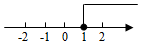 B、
B、 C、
C、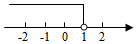 D、
D、 2. 天王星围绕太阳公转的轨道半径为2900000000千米.将数字2900000000千米用科学记数法表示为( )千米。A、0.29×1010 B、2.9×1010 C、2.9×109 D、29×1083. 如图是由个完全相同的小立方体搭成的立体图形,则它的左视图是( )
2. 天王星围绕太阳公转的轨道半径为2900000000千米.将数字2900000000千米用科学记数法表示为( )千米。A、0.29×1010 B、2.9×1010 C、2.9×109 D、29×1083. 如图是由个完全相同的小立方体搭成的立体图形,则它的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、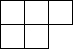 4. 把有理数、在数轴上表示,如图所示,则下列说法正确的是( )
4. 把有理数、在数轴上表示,如图所示,则下列说法正确的是( ) A、 B、 C、 D、5. 与交于、、、 , , , 则的度数( )
A、 B、 C、 D、5. 与交于、、、 , , , 则的度数( ) A、
A、
B、
C、
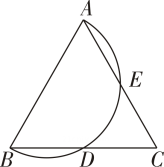
D、6. 如图,在△ABC中,BA=BC,∠B=80°,观察图中尺规作图的痕迹,则∠DCE的度数为( )
 A、60° B、65° C、70° D、75°
A、60° B、65° C、70° D、75°二、填空题(本大题共8小题,共24.0分)
-
7. 分解因式: .8. 如果关于 的方程 有两个相等的实数根,那么 的值是 .9. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行八十步,善行者追之,问几何步及之?”其意思为:速度快的人走100步,速度慢的人只走60步,现速度慢的人先走80步,速度快的人去追赶,则速度快的人要走步才能追到速度慢的人.10. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 ,从木杆的顶端B观察井水水岸D , 视线 与井口的直径 交于点E , 如果测得 米, 米, 米,那么 为米.
 11. 如图,在等边三角形中,为的中点,交于点 , 若 , 则的长为 .
11. 如图,在等边三角形中,为的中点,交于点 , 若 , 则的长为 .
 12. 如图,在平面直角坐标系中,为等腰三角形, , 点到轴的距离为若将绕点逆时针旋转得到 , 则点的坐标为 .
12. 如图,在平面直角坐标系中,为等腰三角形, , 点到轴的距离为若将绕点逆时针旋转得到 , 则点的坐标为 . 13. 若十二边形的每一个内角都相等,那么它的内角的度数是 .14. 若点在抛物线上,则的最大值等于 .
13. 若十二边形的每一个内角都相等,那么它的内角的度数是 .14. 若点在抛物线上,则的最大值等于 .三、解答题(本大题共12小题,共96.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 先化简,再求值: , 其中 .16. 在一个不透明的盒子中装有个小球,个小球上分别标有数字 , , , , 这些小球除数字外其余都相同,现将小球搅拌均匀.
(1)、从盒子中任意抽取一个小球,恰好摸到标有奇数数字小球的概率是多少?
(2)、先从盒子中任意摸一个小球,再从余下的个小球中任意摸一个小球,求摸到的个小球标有的数字之和大于的概率请用树状图或列表的方法求解 .17. 在年南通市老旧小区综合改造工程中,崇川区某街道“雨污分流管网改造”项目需要铺设一条长米的管道,由于天气等各种条件限制,实际施工时,平均每天铺设管道的长度比原计划减少 , 结果推迟天完成求原计划每天铺设管道的长度.18. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , ,求 的大小. 19. 已知图和图中的每个小正方形的边长都是个单位,请在方格纸上按要求画格点三角形:
19. 已知图和图中的每个小正方形的边长都是个单位,请在方格纸上按要求画格点三角形:
 (1)、在图中画 , 使得∽ , 且相似比为:;(2)、在图中画 , 使得∽ , 且面积比为: .20. 对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成、、、四组,绘制了如下统计图表:
(1)、在图中画 , 使得∽ , 且相似比为:;(2)、在图中画 , 使得∽ , 且面积比为: .20. 对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成、、、四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计表组别
分数分
频数
各组总分分

依据以上统计信息解答下列问题:
(1)、求得 , ;
(2)、这次测试成绩的中位数落在组;
(3)、求本次全部测试成绩的平均数.21. 共享单车为大众出行提供了方便,图为单车实物图,图为单车示意图,与地面平行,点、、共线,点、、共线,坐垫可沿射线方向调节.已知 , , 车轮半径为 , 小明体验后觉得当坐垫离地面高度为时骑着比较舒适,求此时的长.结果精确到
参考数据: , , ,
 22. 如图,根据小孔成像的科学原理,当像距小孔到像的距离和物高蜡烛火焰高度不变时,火焰的像高单位:是物距小孔到蜡烛的距离单位:的反比例函数,当时, .
22. 如图,根据小孔成像的科学原理,当像距小孔到像的距离和物高蜡烛火焰高度不变时,火焰的像高单位:是物距小孔到蜡烛的距离单位:的反比例函数,当时, .
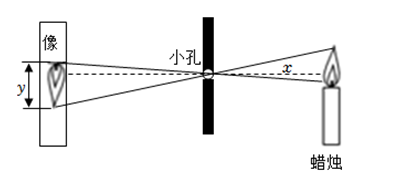 (1)、求关于的函数解析式.
(1)、求关于的函数解析式.
(2)、若火焰的像高为 , 求小孔到蜡烛的距离.23. 如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量千瓦时 , 关于已行驶路程千米的函数图象. (1)、根据图象,蓄电池剩余电量为千瓦时时汽车已经行驶的路程为千米.当时,消耗千瓦时的电量,汽车能行驶的路程为千米.
(1)、根据图象,蓄电池剩余电量为千瓦时时汽车已经行驶的路程为千米.当时,消耗千瓦时的电量,汽车能行驶的路程为千米.
(2)、当时,求关于的函数表达式,并计算当汽车已行驶千米时,蓄电池的剩余电量.24. 如图 , 长方形纸片 , 点位于边上,点位于边上,将纸片沿折叠,点、的对应点分别为点 .
(1)、当点与点重合时,如图 , 如果 , , 连结 , 求的周长;
(2)、如果点位于边上,将纸片沿折叠,点的对应点为点 .
当点恰好落在线段上时,如图 , 求的度数;
当时,直接写出的度数.25. 在矩形中, , , 动点从点出发,沿矩形对角线以每秒个单位长度的速度向终点匀速运动,连结作点关于直线的对称点 , 连结 , 设点的运动时间为秒. (1)、线段的长度为 ;
(1)、线段的长度为 ;
(2)、当点落在的内部时,求的取值范围;
(3)、当、、三点共线时,求的值;
(4)、当与矩形的对角线垂直时,直接写出的值.26. 在平面直角坐标系中,抛物线是常数经过点点在抛物线上,且点的横坐标为 , 过点作轴于点 , 当点与点不重合时,将线段绕点逆时针旋转得到线段 , 以、为邻边构造正方形 .
(1)、求该抛物线对应的函数表达式;
(2)、若点是抛物线上一点,且在抛物线对称轴左侧过点作轴的平行线交抛物线于另一点 , 连接当时,求点的坐标;
(3)、若 , 当抛物线与正方形的边只有个交点,且交点的纵坐标之差为时,求的值;
(4)、当正方形恰有两个顶点在抛物线上时,直接写出的值.