云南省昆明市五华区2023-2024学年高二上学期开学考试数学试题
试卷更新日期:2023-09-22 类型:开学考试
一、选择题;本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合或 , 则( )A、 B、 C、 D、2. 设 , 命题“若 , 则方程有实根”的逆否命题是( )A、若方程有实根,则 B、若方程没有实根,则 C、若方程有实根,则 D、若方程没有实根,则3. 设 , , , 则( )A、 B、 C、 D、4. 中,“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 圆台的上、下底面半径分别是10和20,它的侧面展开图扇环的圆心角为180°,则下面说法不正确的是( )A、圆台的母线长是20 B、圆台的表面积是 C、圆台的高是 D、圆台的体积是6. 如图所示,为了测量湖中两处亭子间的距离,湖岸边现有相距100米的甲、乙两位测量人员,甲测量员在处测量发现亭子位于北偏西亭子位于东北方向,乙测量员在处测量发现亭子位于正北方向,亭子位于北偏西方向,则两亭子间的距离为( )
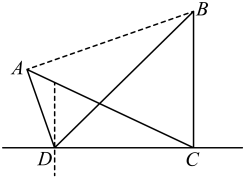 A、米 B、米 C、米 D、米7. 在空间直角坐标系中,已知 , 且平面的法向量为 , 则到平面的距离等于( )A、 B、4 C、 D、8. 已知直线l过点 , 且方向向量为 , 则点到l的距离为( )A、 B、4 C、 D、3
A、米 B、米 C、米 D、米7. 在空间直角坐标系中,已知 , 且平面的法向量为 , 则到平面的距离等于( )A、 B、4 C、 D、8. 已知直线l过点 , 且方向向量为 , 则点到l的距离为( )A、 B、4 C、 D、3二、选择题;本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
9. 如图,E,H分别在线段PA,PD上,C是线段AD的中点,F是线段EH的中点, , PC与EH交于点G,则( )
 A、 B、 C、 D、10. 如图,在棱长为2的正方体中,分别为棱的中点,则( )
A、 B、 C、 D、10. 如图,在棱长为2的正方体中,分别为棱的中点,则( ) A、 B、平面 C、 D、点到平面的距离为11. 如图,在正方体中,为的中点( )
A、 B、平面 C、 D、点到平面的距离为11. 如图,在正方体中,为的中点( ) A、平面 B、 C、若正方体的棱长为1,则点到平面的距离为 D、直线与平面所成角的正弦值为12. 在中,角A、B、C的对边分别为a、b、c,且 , , 有以下四个命题中正确的是( )A、满足条件的不可能是直角三角形 B、面积的最大值为 C、当A=2C时,的周长为 D、当A=2C时,若O为的内心,则的面积为
A、平面 B、 C、若正方体的棱长为1,则点到平面的距离为 D、直线与平面所成角的正弦值为12. 在中,角A、B、C的对边分别为a、b、c,且 , , 有以下四个命题中正确的是( )A、满足条件的不可能是直角三角形 B、面积的最大值为 C、当A=2C时,的周长为 D、当A=2C时,若O为的内心,则的面积为三、填空题;本题共4小题,每小题5分,共20分
-
13. 已知为复数,且 , 则的最大值为.14. 已知 , 则 .15. 在四边形中, , 则四边形的面积为 .16. 如图,正方体的棱长为2,E,F分别为 , 的中点,P是底面上一点.若平面BEF,则AP与平面成角的正弦值的取值范围是 .

四、解答题;本题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
-
17. 已知函数 .
 (1)、请用“五点法”画出函数在一个周期上的图像(先在所给的表格中填上所需的数字,再画图);(2)、求的单调递增区间.18. 某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
(1)、请用“五点法”画出函数在一个周期上的图像(先在所给的表格中填上所需的数字,再画图);(2)、求的单调递增区间.18. 某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图: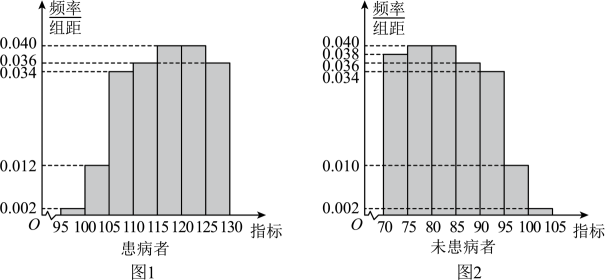
利用该指标制定一个检测标准,需要确定临界值 , 将该指标大于的人判定为阳性,小于或等于的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为 . 假设数据在组内均匀分布.
(1)、当漏诊率时,求临界值和误诊率;(2)、已知一次调查抽取的未患病者样本容量为100,且该项医学指标检查完全符合上面频率分布直方图(图2),临界值 , 从样本中该医学指标在上的未患病者中随机抽取2人,则2人中恰有一人为被误诊者的概率是多少?19. 在四棱锥中,底面是边长为的菱形, , 面 , , , 分别为 , 的中点. (1)、求证:面;(2)、求二面角的大小的正弦值;(3)、求点到面的距离.20. 已知的内角的对边分别为 , , 平分交于点 , 且 .(1)、求;(2)、求的面积.
(1)、求证:面;(2)、求二面角的大小的正弦值;(3)、求点到面的距离.20. 已知的内角的对边分别为 , , 平分交于点 , 且 .(1)、求;(2)、求的面积.
