广东省东莞市重点中学2023-2024学年高二上册数学开学考试试卷

试卷更新日期：2023-09-22 类型：开学考试

进入出卷网下载

一、单选题：本题共8小题，每小题5分，共40分．

1. 为庆祝党的二十大胜利召开，某校举办“学习党的历史，争做新时代好少年”主题教育活动．为评估本次教育活动的效果，拟抽取 $150$ 名同学进行党史测试．已知该校高一学生 $360$ 人，高二学生 $300$ 人，高三学生 $340$ 人，采用分层抽样的方法，应抽取高一学生人数为（）

A、 $60$ B、 $54$ C、 $51$ D、 $45$

查看试题解析
2. 若复数 $z$ 满足 $(1 + z) i = 1 - z$ （ $i$ 为虚数单位），则 $z =$ （）

A、 $- i$ B、 $i$ C、 $1 - i$ D、 $1 + i$

查看试题解析
3. 如图所示的正方形 $O^{'} A^{'} C^{'} B^{'}$ 的边长为 $2 c m$ ，它是水平放置的一个平面图形的直观图，则原图形的面积为（）

A、 $4 \sqrt{2} c m^{2}$ B、 $8 c m^{2}$ C、 $8 \sqrt{2} c m^{2}$ D、 $16 c m^{2}$

查看试题解析
4. 在平面直角坐标系 $x O y$ 中， $A (1 ， 2)$ ， $B (3 ， 3)$ ，则向量 $\vec{A B}$ 在向量 $\vec{O A}$ 上的投影向量为（）

A、 $(- \frac{12}{5} ， - \frac{12}{5})$ B、 $(\frac{4}{5} ， \frac{8}{5})$ C、 $(\frac{8}{5} ， \frac{4}{5})$ D、 $(\frac{12}{5} ， \frac{12}{5})$

查看试题解析
5. 如图所示，直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $∠ B C A = 60 ° ， M ， N$ 分别是 $A_{1} C_{1} ， C C_{1}$ 的中点， $B C = C A = C C_{1}$ ，则 $B N$ 与 $A M$ 所成角的余弦值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{2}{5}$ D、 $\frac{3}{4}$

查看试题解析
6. 某班 $12$ 名篮球队队员的身高（单位： $c m$ ）分别是： $162 ， 170 ， 170 ， 171 ， 181 ， 163 ， 165 ， 179 ， 168 ， 183 ，$ $168 ， 178$ 则第 $85$ 百分位数是（）

A、 $178$ B、 $179$ C、 $180$ D、 $181$

查看试题解析
7. $Δ A B C$ 中， $A C = 3 ， B C = 2 A B$ ，则 $\overset{\leftrightarrow}{C A} \cdot \overset{\leftrightarrow}{C B}$ 的取值范围是（）

A、 $[\frac{9}{2} ， 6]$ B、 $(6 ， 9)$ C、 $[9 ， 18]$ D、 $(6 ， 18)$

查看试题解析
8. 已知三棱锥 $P - A B C$ 的四个顶点在球 $O$ 的球面上， $P A = P B = P C$ ， $Δ A B C$ 是边长为 $2$ 的正三角形， $E 、 F$ 分别是 $P A$ 、 $A B$ 的中点， $E F ⊥$ 平面PAC ，则球 $O$ 的体积为（）

A、 $\frac{\sqrt{6} π}{8}$ B、 $\frac{\sqrt{6} π}{4}$ C、 $\frac{\sqrt{6} π}{2}$ D、 $\sqrt{6} π$

查看试题解析

二、多选题：本题共4小题，每小题5分，共20分．

9. 已知某随机试验的两个随机事件 $A ， B$ 概率满足 $P (A) > 0 ， P (B) > 0$ ，事件 $C =$ “事件 $A$ 与事件 $B$ 恰有一个发生”，则下列命题正确的有（）

A、若 $B = \bar{A}$ ，则 $A ， B$ 是互斥事件 B、若 $A ， B$ 是互为独立事件，则 $A ， B$ 不可能是互斥事件 C、 $P (A ∪ B) > P (C)$ D、 $P (A ∩ B) < P (C)$

查看试题解析
10. 已知 $Δ A B C$ 不是直角三角形，内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，则（）

A、 $s i n C = s i n (A + B)$ B、 $c o s C = c o s (A + B)$ C、 $t a n C = \frac{t a n A + t a n B}{t a n A t a n B - 1}$ D、 $a = b c o s C + c c o s B$

查看试题解析
11. 某保险公司为客户定制了 $5$ 个险种：甲，一年期短期；乙，两全保险；丙，理财类保险；丁，定期寿险；戊，重大疾病保险．各种保险按相关约定进行参保与理赔．该保险公司对 $5$ 个险种参保客户进行抽样调查，得到如图所示的统计图表．则下列说法正确的是（）

A、丁险种参保人数超过五成 B、 $41$ 岁以上参保人数超过总参保人数的五成 C、 $18 - 29$ 周岁人群参保的总费用最少 D、人均参保费用不超过 $5000$ 元

查看试题解析
12. 如图，在等腰梯形 $A B C D$ 中， $A B / / C D$ ， $A B = 2 C D = 2 A D = 2 .$ 将 $Δ A C D$ 沿着 $A C$ 翻折，使得点 $D$ 到点 $P$ ，且 $A P ⊥ B C .$ 下列结论正确的是（）

A、平面 $A P C ⊥$ 平面 $A B C$ B、二面角 $P - A B - C$ 的大小为 $4 5^{°}$ C、三棱锥 $P - A B C$ 的外接球的表面积为 $5 π$ D、点 $C$ 到平面 $A P B$ 的距离为 $\frac{\sqrt{21}}{7}$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

13. 已知采用分层抽样得到的高三男生、女生各100名学生的身高情况为：男生样本平均数为172cm，方差为120，女生样本平均数165cm，方差为120，则总体样本方差是.

查看试题解析
14. 在 $Δ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 $a = x$ ， $b = 10$ ， $c o s A = \frac{3}{5}$ ，则使该三角形有唯一解的 $x$ 的值可以是．（仅需填写一个符合要求的数值）

查看试题解析
15. 某电路由 $A ， B ， C$ 三种部件组成（如图），若在某段时间内 $A ， B ， C$ 正常工作的概率分别为 $\frac{3}{5} ， \frac{2}{3} ， \frac{3}{5}$ ，则该电路正常运行的概率.

查看试题解析
16. 在平面直角坐标系 $x O y$ 中，点 $P$ 为单位圆 $O$ 上的任一点， $M (3 ， 0)$ 、 $N (- 1 ， 1)$ ．若 $\vec{O P} = λ \vec{O M} + μ \vec{O N}$ ，则 $3 λ + μ$ 的最大值为．

查看试题解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 现有 $7$ 名学生，其中 $A_{1}$ ， $A_{2}$ ， $A_{3}$ 的数学成绩优秀， $B_{1}$ ， $B_{2}$ 的物理成绩优秀， $C_{1}$ ， $C_{2}$ 的化学成绩优秀.从中选出数学、物理、化学成绩优秀者各 $1$ 名，组成一个小组代表学校参加竞赛.

(1)、求 $C_{1}$ 被选中的概率；

(2)、求 $A_{1}$ 和 $B_{1}$ 至多有一个被选中的概率

查看试题解析
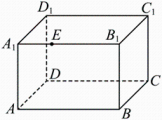18. 如图，在长方体木块 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 6$ ， $B C = 5$ ， $A A_{1} = 4$ ．棱 $A_{1} B_{1}$ 上有一动点 $E$ ．

(1)、若 $A_{1} E = 2$ ，过点 $E$ 画一个与棱 $B C$ 平行的平面 $α$ ，使得 $α$ 与此长方体的表面的交线围成一个正方形 $E F G H$ （其中交线 $G H$ 在平面 $A B C D$ 内）．在图中画出这个正方形 $E F G H$ （不必说出理由），并求平面 $E F G H$ 将长方体分成的两部分的体积比；

(2)、若平面 $A E C_{1}$ 交棱 $C D$ 于 $Q$ ，求四边形 $A E C_{1} Q$ 的周长的最小值．

查看试题解析
19. 现行国家标准 $G B 2762 - 2012$ 中规定了10大类食品中重金属汞的污染限量值，其中肉食性鱼类及其制品中汞的最大残留量为 $1.0 m g / k g$ ，近日某水产市场进口了一批冰鲜鱼2000条，从中随机抽取了200条鱼作为样本，检测鱼体汞含量与其体重的比值 $(m g / k g)$ ，由测量结果制成如图所示的频率分布直方图．

(1)、求 $a$ 的值，并估计这200条鱼汞含量的样本平均数；

(2)、用样本估计总体的思想，估计进口的这批鱼中共有多少条鱼汞含量超标；

(3)、从这批鱼中顾客甲购买了2条，顾客乙购买了1条，甲乙互不影响，求恰有一人购买的鱼汞含量有超标的概率．

查看试题解析
20. 如图，在平面四边形 $A B C D$ 中，点 $B$ 与点 $D$ 分别在直线 $A C$ 的两侧， $B C = C D = 2$ .

(1)、已知 $A B = 2$ ，且 $A C = A D$
当 $c o s ∠ C A D = \frac{2}{3}$ 时，求 $Δ A B C$ 的面积；
②若 $∠ A B C = 2 ∠ A D C > \frac{π}{2}$ ，求 $∠ A B C$ .

(2)、已知 $A D = \sqrt{2} A B$ ，且 $∠ B A D = \frac{π}{4}$ ，求 $A C$ 的最大值.

查看试题解析
21. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是正方形，侧棱 $P D ⊥$ 底面 $A B C D$ ， $P D = D C$ ．

(1)、证明：平面 $P A C ⊥$ 平面 $P B D$ ；

(2)、点 $H$ 在棱 $P C$ 上，当二面角 $H - D B - C$ 的余弦值为 $\frac{1}{3}$ 时，求 $\frac{C H}{C P}$ ．

查看试题解析
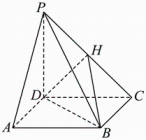22. 地球自西向东自转，造成了太阳每天东升西落运动．因这种现象是地球自转造成的人的视觉效果，所以天文学上把这种运动称为太阳周日视运动，其实质是地球自转的一种反映．研究太阳周日视运动轨迹对分析地球气候、计算当地日出日落时间、理解昼夜长短变化现象、设计建筑物日照时长等有重要意义．太阳周日视运动轨迹与太阳直射地球点有关，也与观测者当地的纬度有关．下图为春分（或秋分）日北纬 $4 5^{∘}$ 某地（如我国哈尔滨、松原、鸡西等地区）的太阳周日视运动轨迹图， $O$ 为当地观测者位置，圆平面 $E S W N$ 是观测者所在的地平面．直线 $P_{1} P_{2}$ 为天轴，其垂直于太阳视运动轨迹所在圆平面 $E A W C$ ，且与直线 $N S$ 在同一圆面上．两直线 $P_{1} P_{2}$ 和 $N S$ 相交于点 $O$ ，夹角 $∠ P_{1} O N$ 为 $45 °$ ．太阳早上 $6 ： 00$ 从正东方 $E$ 点的地平面升起，中午 $12 ： 00$ 处于天空最高点 $A$ ，傍晚 $6 ： 00$ 从正西方 $W$ 点处落入地平面．

(1)、太阳视运动轨迹所在圆平面 $E A W C$ 与地平面 $E S W N$ 所成锐二面角的平面角为多少？

(2)、若图上 $B$ 点为下午 $3 ： 00$ 太阳所在位置，此时阳光入射当地地平面的角度（即直线 $B O$ 与地平面 $E S W N$ 的夹角）为多少？

查看试题解析