云南省昆明市五华区2023-2024学年高三上学期开学考试数学试题
试卷更新日期:2023-09-22 类型:开学考试
一、选择题;本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知是虚数单位,若 , , 则在复平面内的对应点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知曲线在点处的切线方程为 , 则( )A、 B、 C、 D、4. 函数在区间上的图象大致为( )A、
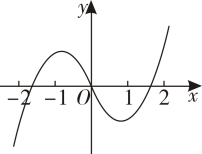 B、
B、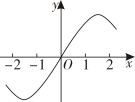 C、
C、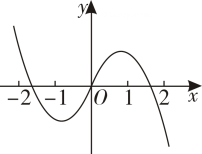 D、
D、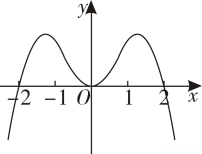 5. 把语文、数学、英语、物理4本书从左到右排成一行,则语文书和英语书不相邻的概率为( )A、 B、1 C、 D、6. 如果 ,那么下列不等式成立的是( )A、 B、 C、 D、7. 已知函数是上的偶函数,且的图象关于点对称,当时, , 则的值为( )A、 B、 C、 D、8. “方斗”常作为盛米的一种容器,其形状是一个上大下小的正四棱台.在综合实践活动中,某小组在超市中测量出一“方斗”的上底面内侧边长为8dm,下底面内侧边长为2dm,侧棱长为6dm.将“方斗”内的大米铺平(即与下底面平行),测得铺平后的大米所在的四边形边长为6dm.已知1kg大米的体积约为 , 则方斗内剩余的大米质量约为(参考数据: , , 结果保留整数)( )A、30kg B、36kg C、45kg D、52kg
5. 把语文、数学、英语、物理4本书从左到右排成一行,则语文书和英语书不相邻的概率为( )A、 B、1 C、 D、6. 如果 ,那么下列不等式成立的是( )A、 B、 C、 D、7. 已知函数是上的偶函数,且的图象关于点对称,当时, , 则的值为( )A、 B、 C、 D、8. “方斗”常作为盛米的一种容器,其形状是一个上大下小的正四棱台.在综合实践活动中,某小组在超市中测量出一“方斗”的上底面内侧边长为8dm,下底面内侧边长为2dm,侧棱长为6dm.将“方斗”内的大米铺平(即与下底面平行),测得铺平后的大米所在的四边形边长为6dm.已知1kg大米的体积约为 , 则方斗内剩余的大米质量约为(参考数据: , , 结果保留整数)( )A、30kg B、36kg C、45kg D、52kg二、选择题;本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
9. 已知变量 , 之间的经验回归方程为 , 且变量 , 的数据如图所示,则下列说法正确的是( )
6
8
10
12
6
m
3
2
A、变量 , 之间呈正相关关系 B、实数m的值等于5 C、该回归直线必过 D、相应于的残差估计值为0.610. 已知则( )A、 B、 C、 D、11. 若 , 则下列命题正确的是( )A、若且 , 则 B、若 , 则 C、若且 , 则 D、12. 设直线与圆 , 则下列结论正确的为( )A、可能将的周长平分 B、若圆上存在两个点到直线的距离为1,则的取值范围为 C、若直线与圆交于两点,则面积的最大值为2 D、若直线与圆交于两点,则中点的轨迹方程为三、填空题;本题共4小题,每小题5分,共20分
-
13. 的展开式中,项的系数为.14. 干支纪年是中国古代的一种纪年法.分别排出十天干与十二地支如下:
天干:甲 乙 丙 丁 戊 己 庚 辛 壬 癸
地支:子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥
把天干与地支按以下方法依次配对:把第一个天干“甲”与第一个地支“子”配出“甲子”,把第二个天干“乙”与第二个地支“丑”配出“乙丑”, , 若天干用完,则再从第一个天干开始循环使用.已知2023年是癸卯年,则年以后是年.
15. 已知 , 则 . (用数字作答)16. 已知函数的最小正周期为 , 将函数的图象向左平移个单位长度,再将所得图象上各点的横坐标缩短为原来的(纵坐标不变),所得函数图象的一条对称轴方程是 , 则的值为 .四、解答题;本题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
-
17. 2022年支付宝“集五福”活动从1月19日开始,持续到1月31日,用户打开支付宝最新版,通过AR扫描“福”字集福卡(爱国福、富强福、和谐福、友善福、敬业福),在除夕夜22:18前集齐“五福”的用户获得一个大红包.某研究型学习小组为了调查研究“集五福与性别是否有关”,现从某一社区居民中随机抽取200名进行调查,得到统计数据如下表所示:
集齐“五福”卡
末集齐“五福”卡
合计
男性
80
20
100
女性
65
35
100
合计
145
55
200
参考公式: , 其中 .
0.10
0.050
0.010
0.001
2.706
3.841
6.635
10.828
(1)、请根据以上数据,由的独立性检验,判断集齐“五福”是否与性别有关;(2)、现采用分层抽样的方法从男性的样本中抽取5人,再从这5人中随机抽取3人,求这3人中恰有1人未集齐“五福”卡的概率.18. 已知函数( , 且)的图象经过点 , .(1)、求函数的解析式;(2)、设函数 , 求函数的值域19. 某学校为推动学校的大课间运动,开始在部分班级中使用一套新的大课间运动体操(记为A类体操),原来的大课间运动体操(记为B类体操),为了解学生对大课间运动的喜爱程度与使用大课间运动体操类别是否有关,分别对使用A类体操与B类体操的学生进行了问卷调查,现分别随机抽取了100个学生的问卷调查情况,得到如下数据:喜爱
不喜爱
A类体操
70
30
B类体操
40
60
附: ,
(1)、试根据小概率值的独立性检验,能否认为喜爱大课间运动程度与A类体操和B类体操有关?(2)、从样本的喜爱大课间运动的学生中,按A、B类分层抽取11名学生参加一个座谈会,再从中抽取3名学生在学生大课间运动会上发言,求参加发言的学生既有喜爱A类体操也有喜爱B类体操的概率.20. 现有甲、乙两名运动员争夺某项比赛的奖金,规定两名运动员谁先赢局,谁便赢得全部奖金a元.假设每局甲赢的概率为 , 乙赢的概率为 , 且每场比赛相互独立.在甲赢了局,乙赢了局时,比赛意外终止,奖金如何分配才合理?评委给出的方案是:甲、乙按照比赛再继续进行下去各自赢得全部奖金的概率之比分配奖金.(1)、若 , 求;(2)、记事件A为“比赛继续进行下去乙赢得全部奖金”,试求当时,比赛继续进行下去甲赢得全部奖金的概率 , 并判断当时,事件A是否为小概率事件,并说明理由.规定:若随机事件发生的概率小于0.06,则称该随机事件为小概率事件.
