黑龙江省鹤岗市2023-2024学年高三上册数学开学试卷

试卷更新日期：2023-09-22 类型：开学考试

进入出卷网下载

一、单选题（本题共8个小题，每题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 若集合 $A = {x \in N | 2 \leq x \leq 3}$ ， $B = {2 ， 3 ， 4 ， 5}$ ，则 $A ∪ B =$ （）

A、 ${2 ， 3 ， 4 ， 5}$ B、 ${2 ， 3}$ C、 ${2 ， 4 ， 5}$ D、 $R$

查看试题解析
2. 已知 $△ A B C$ 中， $a = 2 ， b = 2 \sqrt{3} ， B = \frac{π}{3}$ ，则角 $A$ 的值是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{6}$ 或 $\frac{5 π}{6}$ D、 $\frac{π}{3}$ 或 $\frac{2 π}{3}$

查看试题解析
3. 已知角 $α$ 的终边上一点 $A (4 ， 3)$ ，且 $t a n (α + β) = 2$ ，则 $t a n (3 π - β) =$ （）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{5}{2}$ D、 $- \frac{5}{2}$

查看试题解析
4. 北京时间2023年2月10日0时16分，经过约7小时的出舱活动，神舟十五号航天员费俊龙、邓清明、张陆密切协同，圆满完成出舱活动全部既定任务，出舱活动取得圆满成功．载人飞船进入太空需要搭载运载火箭，火箭在发射时会产生巨大的噪声，已知声音的声强级 $d (x)$ （单位： $d B$ ）与声强 $x$ （单位： $W / m^{2}$ ）满足关系式： $d (x) = 10 l g \frac{x}{1 0^{- 12}}$ ．若某人交谈时的声强级约为 $60 d B$ ，且火箭发射时的声强与此人交谈时的声强的比值约为 $1 0^{7.8}$ ，则火箭发射时的声强级约为（）

A、 $125 d B$ B、 $132 d B$ C、 $138 d B$ D、 $156 d B$

查看试题解析
5. 已知角A、B、C为 $△ A B C$ 的三个内角，若 $s i n (\frac{A + B - C}{2}) = s i n (\frac{A - B + C}{2})$ ，则 $△ A B C$ 一定是（）

A、等腰直角三角形 B、直角三角形 C、等腰三角形 D、等腰或直角三角形

查看试题解析
6. 把函数 $y = c o s (\frac{π}{2} x)$ 图象上所有点的横坐标都伸长为原来的2倍，纵坐标不变，再把所得图象向右平移2个单位长度，得到函数 $f (x)$ 的图象，则 $f (1) + f (2) + f (3) + ⋯ + f (2023) =$ （）

A、 $- 1$ B、 $- \frac{\sqrt{2}}{2}$ C、0 D、1

查看试题解析
7. 已知函数 $f (x) = m^{2} c o s x - m \cdot 2^{x + 1}$ 的图象和函数 $g (x) = \frac{m}{2^{x - 1}} - 3$ 的图象有唯一交点，则实数m的值为（）

A、1 B、3 C、 $- 1$ 或3 D、1或3

查看试题解析
8. $a = \frac{1}{11} ， b = l n 1.1 ， c = t a n 0.1$ ，则（）

A、 $c < a < b$ B、 $a < c < b$ C、 $b < a < c$ D、 $a < b < c$

查看试题解析

二、多选题（本题共4个小题，每题5分，共20分）

9. 已知函数 $f (x)$ 是定义在 $R$ 上的奇函数，且 $f (1 + x) = f (1 - x)$ ．当 $0 < x \leq 1$ 时， $f (x) = 3^{x} - 1$ ，则（）

A、 $f (x)$ 是周期为2的周期函数 B、 $f (x)$ 的值域为 $[- 2 ， 2]$ C、 $x = 3$ 是 $f (x)$ 图象的一条对称轴 D、 $f (x)$ 的图象关于点 $(- 2 ， 0)$ 对称

查看试题解析
10. 已知 $3^{x} = 4^{y} = 12$ ，则实数 $x ， y$ 满足（）

A、 $x > y$ B、 $x + y < 4$ C、 $\frac{1}{x} + \frac{1}{y} < \frac{1}{2}$ D、 $x y > 4$

查看试题解析
11. 已知 $f (x) = c o s x (c o s x + \sqrt{3} s i n x)$ ，下列结论正确的是（）

A、 $f (x)$ 的最小正周期为 $2 π$ B、把 $f (x)$ 的图象向左平移 $\frac{π}{6}$ 个单位长度，得到的图象关于 $y$ 轴对称 C、若 $f (x)$ 在区间 $[- \frac{π}{6} ， m]$ 上的最大值是 $\frac{3}{2}$ ，则 $m$ 的最小值为 $\frac{π}{3}$ D、若 $x_{1} + x_{2} = \frac{5 π}{6}$ ，则 $f (x_{1}) + f (x_{2}) = 1$

查看试题解析
12. 函数 $f (x) = k x - | s i n x |$ 在 $(0 ， + \infty)$ 上有两个零点 $α ， β (α < β)$ ，下列说法正确的是（）

A、 $β \in (\frac{5 π}{4} ， \frac{3 π}{2})$ B、 $t a n β - α = \frac{s i n α + s i n β}{k}$ C、 $t a n (β + \frac{π}{4}) = \frac{1 + β}{1 - β}$ D、 $f (x)$ 在 $(0 ， 2 π)$ 上有2个极值点 $x_{1} ， x_{2} (x_{1} < x_{2})$ 且 $x_{2} - x_{1} = π$

查看试题解析

三、填空题（本题共4个小题，每小题5分，共20分）

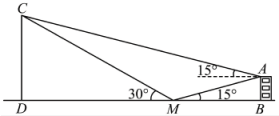
13. 幂函数 $f (x) = (m^{2} - 2 m - 2) x^{m}$ 在 $(0 ， + \infty)$ 上单调递增，则 $g (x) = l o g_{a} (x - m) + 1$ （ $a > 0$ 且 $a \neq 1$ ）的图象过定点．

查看试题解析
14. 某同学为了测量学校天文台 $C D$ 的高度，选择学校宿舍楼三楼一阳台 $A$ ， $A$ 到地面的距离 $A B$ 为 $30 (2 - \sqrt{3}) m$ ，在它们之间的地面上的点M（B、M、D三点共线）处测得阳台 $A$ ，天文台顶 $C$ 的仰角分别是 $15 °$ 和 $30 °$ ，在用台 $A$ 处测得天文台顶 $C$ 的仰角为 $15 °$ ，假设 $A B$ 、 $C D$ 和点 $M$ 在同一平面内，则学校天文台 $C D$ 的高度为 $m$ ．

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} | x^{2} + 2 x | ， x \leq 0 \\ \frac{1}{x} ， x > 0 \end{array}$ ，若关于 $x$ 的方程 $f (x) = a (x + 3)$ 有四个不同的实数根，则实数 $a$ 的取值范围是．

查看试题解析
16. 锐角 $△ A B C$ 中，内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c ， a = 1$ ，且 $b c o s A - c o s B = 1$ ，则 $s i n B + 2 \sqrt{3} s i n^{2} A$ 的取值范围为．

查看试题解析

四、解答题（本题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤）

17. 已知函数 $f (x) = s i n (2 x + \frac{π}{3}) + s i n (2 x - \frac{π}{3}) + \sqrt{3} c o s 2 x$

(1)、求函数 $f (x)$ 的最小正周期；

(2)、当 $x \in [0 ， \frac{π}{2}]$ 时，求函数 $f (x)$ 的单调递减区间．

查看试题解析
18. 已知函数 $f (x) = 2 s i n (ω x + φ) (ω > 0 ， 0 < φ < \frac{π}{2})$ 的部分图象如图所示．该图象与 $y$ 轴交于点 $A (0 ， \sqrt{3})$ ，与 $x$ 轴交于 $B ， C$ 两点， $D$ 为图象的最高点，且 $△ B C D$ 的面积为 $\frac{π}{2}$ ．

(1)、求 $f (x)$ 的解析式及其单调递增区间．

(2)、若将 $f (x)$ 的图象向右平移 $\frac{π}{12}$ 个单位长度，再将所得图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），得到函数 $g (x)$ 的图象．若 $g (α) = \frac{8}{5} (\frac{π}{2} < α < π)$ ，求 $c o s (α + \frac{π}{6})$ 的值．

查看试题解析
19. 已知函数 $f (x) = x + \frac{1}{2} ， S_{n} = f (\frac{1}{n}) + f (\frac{2}{n}) + ⋯ + f (\frac{n - 2}{n}) + f (\frac{n - 1}{n})$ ，其中 $n \in N^{*}$ ，且 $n \geq 2$ ．

(1)、当 $n \geq 2$ 时，求 $S_{n}$ ；

(2)、设 $a_{1} = \frac{1}{2} ， a_{n} = \frac{1}{(S_{n} + 1) (S_{n + 1} + 1)} (n \in N^{*} ， n \geq 2)$ ，记数列 ${a_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，求使得 $T_{n} < \frac{m}{2}$ 恒成立的 $m$ 的最小正整数．

查看试题解析
20. 射影几何学中，中心投影是指光从一点向四周散射而形成的投影，如图， $O$ 为透视中心，平面内四个点 $E ， F ， G ， H$ 经过中心投影之后的投影点分别为 $A ， B ， C ， D$ ．对于四个有序点 $A ， B ， C ， D$ ，定义比值 $x = \frac{\frac{C A}{C B}}{\frac{D A}{D B}}$ 叫做这四个有序点的交比，记作 $(A B C D)$ ．

(1)、证明： $(E F G H) = (A B C D)$ ；

(2)、已知 $(E F G H) = \frac{3}{2}$ ，点 $B$ 为线段 $A D$ 的中点， $A C = \sqrt{3} O B = 3 ， \frac{s i n ∠ A C O}{s i n ∠ A O B} = \frac{3}{2}$ ，求 $c o s A$ ．

查看试题解析
21. 已知椭圆 $C_{1} ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点与抛物线 $C_{2} ： y^{2} = 2 p x ， (p > 0)$ 的焦点重合， $C_{1}$ 的离心率为 $\frac{1}{2}$ ，过 $C_{1}$ 的右焦点 $F$ 且垂直于 $x$ 轴的直线截 $C_{2}$ 所得的弦长为4．

(1)、求椭圆 $C_{1}$ 和抛物线 $C_{2}$ 的方程；

(2)、过点 $M (3 ， 0)$ 的直线 $l$ 与椭圆 $C_{1}$ 交于 $A ， B$ 两点，点 $B$ 关于 $x$ 轴的对称点为点 $E$ ，证明：直线 $A E$ 过定点．

查看试题解析
22. 已知函数 $f (x) = a l n \frac{x}{a} - x ， g (x) = a x - a e^{x}$ ．（ $e = 2.71828 ⋯$ 为自然对数的底数）

(1)、当 $a = 1$ 时，求函数 $y = f (x)$ 的极大值；

(2)、已知 $x_{1} ， x_{2} \in (0 ， + \infty)$ ，且满足 $f (x_{1}) > g (x_{2})$ ，求证： $x_{1} + a e^{x_{2}} > 2 a$ ．

查看试题解析