专题1.3二次函数的图像性质(二)【八大题型】2023~2024学年九年级上册数学第1章二次函数(浙教版)
试卷更新日期:2023-09-21 类型:同步测试
一、利用二次函数图像性质判断函数值大小
-
1. 已知 , , 三点都在二次函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、2. 若二次函数的图象经过A、B、C三点,则关于y1、y2、y3大小关系正确的是( )A、 B、 C、 D、3. 已知抛物线 , , , 是抛物线上三点,则 , , 由小到大序排列是( )A、 B、 C、 D、4. 已知点 , 在二次函数的图像上,若 , 则必有( )A、 B、 C、 D、
二、利用二次函数图像性质求参数特定值或取值范围
-
5. 已知二次函数的图像与 轴无交点,则 的取值范围是( )A、 B、 C、 D、 且6. 已知二次函数的图象经过点和.(1)、求 , 满足的关系式;(2)、当自变量的值满足时,随的增大而增大,求的取值范围;(3)、若函数图象与轴无交点,求的取值范围.7. 已知二次函数(为实数,且),当时,随增大而减小,则实数的取值范围是( )A、 B、 C、 D、8. 二次函数中当时随的增大而增大,则一次项系数满足( )A、 B、 C、 D、
三、根据分段函数最值求参数的值
-
9. 二次函数(为实数,且),对于满足的任意一个的值,都有 , 则的最大值为( )A、 B、 C、2 D、10. 当-2≤x≤1时,关于x的二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )A、2 B、2或 C、2或或- D、2或或-11. 已知二次函数 , 当时,有最大值及最小值 , 当时,实数的值为( )A、-3或-1或5 B、-3或5 C、-1或 D、-3或或512. 已知二次函数 , 若时,函数的最大值与最小值的差为4, 则a的值为( )A、 B、 C、或 D、1或13. 已知函数(b,c为常数)的图像经过点 , .(1)、求b,c的值;(2)、当时,求y的最大值与最小值之差;(3)、当时,若y的最大值与最小值之差为8,求k的值.
四、根据分段函数的最值求参数取值范围
-
14. 已知二次函数 , 当时,y有最小值和最大值5,则m的取值范围为( )A、 B、 C、 D、15. 已知函数在的最大值是1,最小值是 , 则m的取值范围是.
五、利用二次函数图像性质求最值
-
16. 已知抛物线 , 则当时,函数的最大值为( )A、 B、 C、0 D、217. 在平面直角坐标系中,二次函数为常数的图象经过点 , 其对称轴在轴左侧,则该二次函数有( )A、最大值 B、最大值 C、最小值 D、最小值18. 在平面直角坐标系中,设二次函数 , (a,b;是实数,)的最小值分别为m和n,若 , 则的值为( )A、0 B、 C、 D、19. 已知二次函数的图象经过点 , 且满足.当时,该函数的最大值m和最小值n之间满足的关系式是( )A、 B、 C、 D、
六、二次函数对称性的运用
-
20. 如图,在平面直角坐标系中,正方形的边与x轴重合,顶点 A、D在抛物线上.若抛物线的顶点到x轴的距离比长4,则c的值为 .
 21. 如图,在平面直角坐标系中,正方形的点在轴的负半轴上,抛物线的顶点为 , 且经过点、 . 若为等腰直角三角形,则的值是 .
21. 如图,在平面直角坐标系中,正方形的点在轴的负半轴上,抛物线的顶点为 , 且经过点、 . 若为等腰直角三角形,则的值是 . 22. 如图,正方形、的顶点D、F都在抛物线上,点B、C、E均在y轴上.若点O是边的中点,则正方形的边长为 .
22. 如图,正方形、的顶点D、F都在抛物线上,点B、C、E均在y轴上.若点O是边的中点,则正方形的边长为 .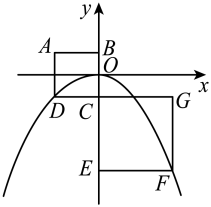 23. 如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数与的图象,则阴影部分的面积是 .
23. 如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数与的图象,则阴影部分的面积是 .
七、二次函数与一次函数图像共存问题
-
24. 在同一平面直角坐标系中,一次函数与二次函数的图象大致为( )A、
 B、
B、 C、
C、 D、
D、 25. 一次函数与二次函数在同一平面直角坐标系中的图象可能是( )A、
25. 一次函数与二次函数在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 26. 在同一坐标系中,一次函数与二次函数的图象可能是( )A、
26. 在同一坐标系中,一次函数与二次函数的图象可能是( )A、 B、
B、 C、
C、 D、
D、 27. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象为( )A、
27. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象为( )A、 B、
B、 C、
C、 D、
D、
八、二次函数图像与系数关系的一般性结论
-
28. 如图,抛物线的对称轴为直线 , 经过点 . 下列结论:①;②;③;④抛物线经过点和 , 则;⑤(为任意实数).其中,正确结论的个数是( )
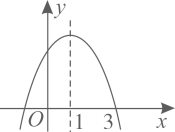 A、1 B、2 C、3 D、429. 二次函数 (a、b、c是常数,且 )的图象如图所示,对称轴为直线 .下列结论:① ;② ;③ ;④ .其中正确的个数为( )
A、1 B、2 C、3 D、429. 二次函数 (a、b、c是常数,且 )的图象如图所示,对称轴为直线 .下列结论:① ;② ;③ ;④ .其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个