专题1.2二次函数的图像性质（一）【八大题型】2023~2024学年九年级上册数学第1章二次函数（浙教版）-在线组卷题库

1. 二次函数 $y = x^{2} - 2 x + 4$ 化为 $y = a (x - h)^{2} + k$ 的形式，下列正确的是（）

A、 $y = (x - 1)^{2} + 2$ B、 C、 $y = (x - 2)^{2} + 2$ D、 $y = (x - 2)^{2} + 4$

查看试题解析
2. 将抛物线 $y = x^{2} - 4 x - 1$ 化成顶点式为．

查看试题解析
3. 将二次函数 $y = 2 x^{2} + 4 x - 1$ 的解析式化为 $y = a (x + m)^{2} + k$ 的形式，并指出该函数图象的开口方向、顶点坐标和对称轴．

查看试题解析

4. 对于抛物线 $y = - 2 (x - 1)^{2} + 3$ ，下列判断正确的是（）

A、抛物线的开口向上 B、抛物线的顶点坐标是 $(- 1 ， 3)$ C、对称轴为直线 $x = 1$ D、当 $x = 3$ 时， $y > 0$

查看试题解析
5. 抛物线y=2(x-3)²+7的对称轴为（）

A、直线x=3 B、直线x=-3 C、直线x=2 D、直线x=7

查看试题解析
6. 下列对于二次函数 $y = - x^{2} + 1$ 图象描述中，正确的是（　　）

A、开口向上 B、对称轴是y轴 C、图象有最低点 D、在对称轴右侧的图象从左往右呈上升趋势

查看试题解析
7. 表中列出的是一个二次函数的自变量x与函数y的几组对应值：
x
…
          $- 2$
0
1
3
…
y
…
6
          $- 4$
          $- 6$
          $- 4$
…
下列各选项中，正确的是（　　）

A、这个函数的最小值为 $- 6$ B、这个函数的图象开口向下 C、这个函数的图象与x轴无交点 D、当 $x > 2$ 时，y的值随x值的增大而增大

查看试题解析

8. 已知二次函数 $y = 2 x^{2} - 4 x - 1$ ．

(1)、用配方法求这个二次函数的顶点坐标；

(2)、在所给的平面直角坐标系 $x O y$ 中（如图），画出这个二次函数的图象；

(3)、请描述这个二次函数图象的变化趋势．

查看试题解析

9. 已知一个二次函数图象上部分点的横坐标

x

与纵坐标

y

的对应值如表所示：

$x$	$\dots$	$- 3$	$- 2$	$- 1$	$0$	$1$	$\dots$
$y$	$\dots$	$0$	$- 3$	$- 4$	$- 3$	$0$	$\dots$

(1)、这个二次函数的解析式是；

(2)、在给定的平面直角坐标系中画出这个二次函数的图象；

(3)、当

- 4 < x < 0

时，

y

的取值范围为．

查看试题解析

10. 已知抛物线 $y = - x^{2} + 2 x + 3$ ，将这条抛物线向左平移3个单位，再向下平移2个单位．

(1)、求平移后新抛物线的表达式和它的开口方向、顶点坐标、对称轴，并说明它的变化情况；

(2)、在如图所示的平面直角坐标系内画出平移后的抛物线．

查看试题解析

11. 一班数学兴趣小组对函数

y = x^{2} - 2 | x | - 3

的图象和性质进行了探究，探究过程如下，请补充完整：

$x$	…	-3	$- \frac{5}{2}$	-2	-1	0	1	2	$\frac{5}{2}$	3	…
$y$	…	0	$- \frac{7}{4}$	$m$	-4	-3	-4	-3	$- \frac{7}{4}$	0	…

(1)、自变量

x

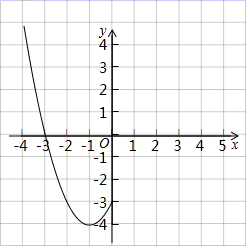
的取值范围是全体实数，

x

与

y

的几组对应值见表：其中，

m =

.

(2)、根据表中数据，在所示的平面坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分.

(3)、观察函数

y = x^{2} - 2 | x | - 3

图象，回答下列问题：

①函数图象的对称性是：.

②当 $x > 0$ 时，写出 $y$ 随 $x$ 的变化规律：.

③进一步探究图象发现：方程 $x^{2} - 2 | x | - 3 = - 3$ 的根为.

查看试题解析

12. 如图1，在平面直角坐标系xOy中，抛物线y＝ax²+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点(x，y)的坐标值：
x
…
﹣1
0
1
2
3
…
y
…
0
3
4
3
0
…
则这条抛物线的解析式为．

查看试题解析
13. 已知抛物线的顶点坐标为（－1，2），与y轴交于点（0， $\frac{3}{2}$ ）

(1)、求二次函数的解析式；

(2)、判断点P（2，－ $\frac{5}{2}$ ）是否落在抛物线上，请说明理由.

查看试题解析
14. 在如图所示的直角坐标系中，已知正方形 $A B C D$ 的边长为 $4$ ，且 $D (2 ， 2)$ ，

(1)、求图像经过 $B$ ， $E$ ， $F$ 三点的二次函数的表达式；

(2)、求（1）中二次函数图象的顶点坐标．

查看试题解析

15. 设二次函数

y = a x^{2} + b x + 1

，（

a \neq 0

，

b

是实数）．已知函数值

y

和自变量

x

的部分对应取值如下表所示：

$x$	…	$- 1$	0	1	2	3	…
$y$	…	$m$	1	$n$	1	$p$	…

(1)、若

m = 4

，求二次函数的表达式；

(2)、写出一个符合条件的

x

的取值范围，使得

y

随

x

的增大而减小．

(3)、若在m、n、p这三个实数中，只有一个是正数，求

a

的取值范围．

查看试题解析

16. 要得到二次函数 $y = - x^{2} + 2 x - 2$ 图象，需将 $y = - x^{2}$ 的图象（）

A、先向左平移2个单位，再向下平移2个单位 B、先向右平移2个单位，再向上平移2个单位 C、先向左平移1个单位，再向上平移1个单位 D、先向右平移1个单位，再向下平移1个单位

查看试题解析
17. 将抛物线平移，若有一个点既在平移前的抛物线上，又在平移后的抛物线上，则称这个点为“平衡点”，现将抛物线 $C_{1}$ ： $y = {(x - 1)}^{2} - 3$ 向右平移m（ $m > 0$ ）个单位长度后得到新的抛物线 $C_{2}$ ，若 $(3 ， n)$ 为“平衡点”，则m的值为（）

A、4 B、3 C、2 D、1

查看试题解析
18. 将抛物线 $y = x^{2} + 4 x - 4$ 向下平移3个单位长度，再向左平移2个单位长度，得到抛物线的表达式为.

查看试题解析
19. 如图，抛物线 $y = \frac{1}{3} {(x - 4)}^{2} + h$ 与x轴的一个交点为 $A (6 ， 0)$ ，与y轴交于点B.

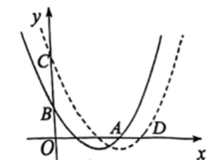(1)、求h的值及点B的坐标.

(2)、将该抛物线向右平移 $m (m > 0)$ 个单位长度后，与y轴交于点C，且点A的对应点为D，若 $O C = O D$ ，求m的值.

查看试题解析
20. 如图，在平面直角坐标系 $x O y$ 中，已知抛物线 $y = a x^{2} + b x (a > 0)$ 的顶点为 $C$ ，与 $x$ 轴的正半轴交于点 $A$ ，它的对称轴与抛物线 $y = a x^{2} (a > 0)$ 交于点 $B$ ．若四边形 $A B O C$ 是正方形，则 $b$ 的值是．

查看试题解析

21. 二次函数y=2x²-12x+5关于x轴对称的图象所对应的函数化成顶点式为.

查看试题解析
22. 若抛物线 $L ： y = x^{2} + (b - 1) x - 3$ 与抛物线 $L^{'} ： y = x^{2} - 10 x + 3 c$ 关于直线 $x = 2$ 对称，则 $b - c$ 的值为（）

A、3 B、7 C、 $- 4$ D、4

查看试题解析
23. 把二次函数 $y = a x^{2} + b x + c (a > 0)$ 的图象作关于y轴的对称变换，所得图象的解析式为 $y = a {(x + 1)}^{2} - a^{2}$ ，若 $(m - 2) a + b + c \geq 0$ 成立，则m的最小整数值为（）

A、2 B、3 C、4 D、5

查看试题解析
24. 规定：如果两个函数的图象关于 $y$ 轴对称，那么称这两个函数互为“ $Y$ 函数” $.$ 例如：函数 $y = x + 3$ 与 $y = - x + 3$ 互为“ $Y$ 函数” $.$ 若函数 $y = \frac{k}{4} x^{2} + (k - 1) x + k - 3$ 的图象与 $x$ 轴只有一个交点，则它的“ $Y$ 函数”图象与 $x$ 轴的交点坐标为．

查看试题解析

25. 若拋物线 $y = x^{2} + 2 a x + {(a - 1)}^{2}$ 的顶点在第二象限，则 $a$ 的取值范围是（）

A、 $0 < a < \frac{1}{2}$ B、 $a > 0$ C、 $a > \frac{1}{2}$ D、 $a < 0$

查看试题解析
26. 将二次函数 $y = a x^{2} - 8 a x + 2$ 的图象向左平移m个单位后过点 $(5 ， 2)$ ，则m的值为（）

A、2 B、3 C、4 D、5

查看试题解析
27. 已知点 $P (m ， n)$ 在二次函数 $y = x^{2} + 4$ 的图象上，则 $m - n$ 的最大值等于.

查看试题解析
28. 已知抛物线 $y = x^{2} - 2 (k + 1) x + 4$ 的顶点在y轴上，则k的值是.

查看试题解析
29. 已知二次函数 $y = a x^{2} - 2 a x - a^{2} + 4 a - 11$ （a是常数，且 $a \neq 0$ ）．

(1)、该二次函数图象的对称轴是；

(2)、该二次函数图象与y轴交点的纵坐标的最大值为．

查看试题解析

30. 二次函数 $y = a x^{2} + 4 x + 1$ （ $a$ 为实数，且 $a < 0$ ），对于满足 $0 \leq x \leq m$ 的任意一个 $x$ 的值，都有 $- 2 ≤ y ≤ 2$ ，则 $m$ 的最大值为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、2 D、 $\frac{3}{2}$

查看试题解析
31. 已知二次函数 $y = a x^{2} - 4 a x + 5 (a > 0)$ ，当 $0 \leq x \leq m$ 时，y有最小值 $- 4 a + 5$ 和最大值5，则m的取值范围为（）

A、 $m \geq 2$ B、 $0 \leq m \leq 2$ C、 $1 \leq m \leq 2$ D、 $2 \leq m \leq 4$

查看试题解析
32. 已知抛物线 $y = a x^{2} + b x + c (a$ 、 $b$ 、 $c$ 是常数， $a \neq 0)$ 经过点 $A (1 ， 0)$ 和点 $B (0 ， - 3)$ ，若该抛物线的顶点在第三象限，记 $m = 2 a - b + c$ ，则 $m$ 的取值范围是（）

A、 $0 < m < 3$ B、 $- 6 < m < 3$ C、 $- 3 < m < 6$ D、 $- 3 < m < 0$

查看试题解析
33. 已知函数 $y = x^{2} + x - 1$ 在 $m \leq x \leq 1$ 的最大值是1，最小值是 $- \frac{5}{4}$ ，则m的取值范围是.

查看试题解析

专题1.2二次函数的图像性质（一）【八大题型】2023~2024学年九年级上册数学第1章二次函数（浙教版）

一、二次函数的解析式互化

二、根据二次函数解析式判断图像性质

三、五点作图法绘“函数图像”

四、待定系数法求二次函数解析式

五、二次函数的平移变换

六、二次函数的对称变化

七、利用二次函数对称轴、最值求参数值

八、利用二次函数增减性求参数范围