湖北省荆门市202-2023学年八年级下学期数学期末试卷
试卷更新日期:2023-09-21 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分。在每小题中均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号涂在答题卡上)
-
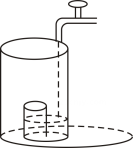
1. 下列计算正确的是( )A、 B、 C、 D、2. 平行四边形、矩形、菱形、正方形都具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线互相垂直平分且相等3. 下列根式中属于最简二次根式的是( )A、 B、 C、 D、4. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水如图,则小水杯内水面的高度与注水时间的函数图象大致为( )
 A、
A、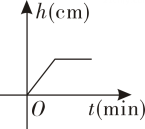 B、
B、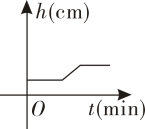 C、
C、 D、
D、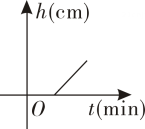 5. 如图是某学校全体教职工年龄的频数分布直方图(每组年龄包含最小值,不包含最大值),根据图形提供的信息,下列说法中错误的是( )
5. 如图是某学校全体教职工年龄的频数分布直方图(每组年龄包含最小值,不包含最大值),根据图形提供的信息,下列说法中错误的是( )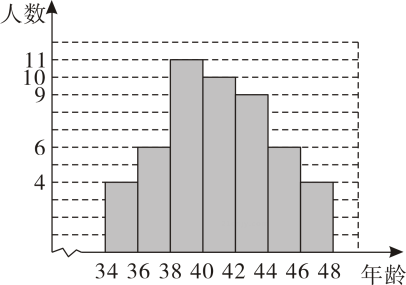 A、该学校教职工总人数是50人 B、这一组年龄在小组的教职工人数占该学校全体教职工总人数的 C、教职工年龄的中位数一定落在这一组 D、教职工年龄的众数一定在这一组6. 如图,数学实践活动课上小明用两根木条钉成一个角形框架 , 且 , , 将一根橡皮筋两端固定在点A,B处,拉展成线段AB,在平面内,拉动橡皮筋上的一点 , 当四边形OACB是菱形时,橡皮筋再次被拉长了( )
A、该学校教职工总人数是50人 B、这一组年龄在小组的教职工人数占该学校全体教职工总人数的 C、教职工年龄的中位数一定落在这一组 D、教职工年龄的众数一定在这一组6. 如图,数学实践活动课上小明用两根木条钉成一个角形框架 , 且 , , 将一根橡皮筋两端固定在点A,B处,拉展成线段AB,在平面内,拉动橡皮筋上的一点 , 当四边形OACB是菱形时,橡皮筋再次被拉长了( )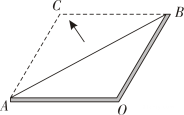 A、 B、 C、 D、7. 如图,在四边形ABCD中,点E,F,G,H分别AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )
A、 B、 C、 D、7. 如图,在四边形ABCD中,点E,F,G,H分别AD,BD,BC,CA的中点,若四边形EFGH是矩形,则四边形ABCD需满足的条件是( )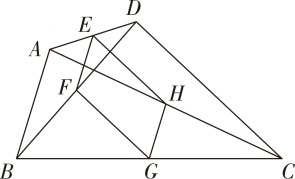 A、AC=BD B、AB⊥DC C、AC⊥BD D、AB=DC8. 如图,直线y=x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA边上的一个动点,当PC+PD值最小时,点P的坐标为( )
A、AC=BD B、AB⊥DC C、AC⊥BD D、AB=DC8. 如图,直线y=x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA边上的一个动点,当PC+PD值最小时,点P的坐标为( )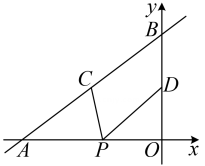 A、 B、(-6,0) C、 D、9. 在同一平面直角坐标系中,一次函数的与的图象可能是( )A、
A、 B、(-6,0) C、 D、9. 在同一平面直角坐标系中,一次函数的与的图象可能是( )A、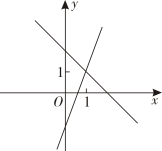 B、
B、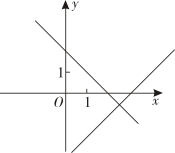 C、
C、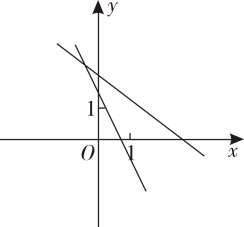 D、
D、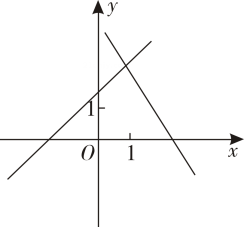 10. 如图,正方形ABCD的边长为4,对角线AC、BD相交于点 , 将绕点顺时针旋转得到交CD于点连接BG交AC于 , 连接EH.则下列结论:
10. 如图,正方形ABCD的边长为4,对角线AC、BD相交于点 , 将绕点顺时针旋转得到交CD于点连接BG交AC于 , 连接EH.则下列结论:①EG=CG=CF;②四边形EHCG是菱形;③△BDG的面积是;④;其中正确的是( )
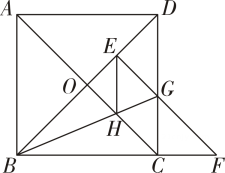 A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题(本大题共6小题,每小题3分,共18分.请将结果直接填写在答题卡相应位置)
-
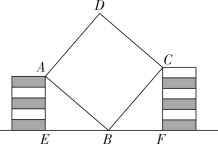
11. 已知一组数据6,5,3,3,5,2,则这组数据的平均数是.12. 若代数式在实数范围内有意义,则的取值范围是.13. 八年级数学兴趣小组用11块高度都是的相同长方体小木块垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD木板,截面如图所示.两木墙高分别为AE与CF,点在EF上,则正方形ABCD木板的面积为..
 14. 一次函数与的图象如图所示,则下列结论:①;②a<0,b>0;③当时,;④不等式的解集是 , 其中正确的结论有.
14. 一次函数与的图象如图所示,则下列结论:①;②a<0,b>0;③当时,;④不等式的解集是 , 其中正确的结论有.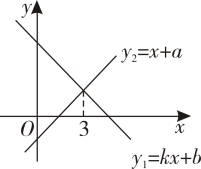 15. 如图,在Rt中,为边BC上一个动点不与B、C重合),PE⊥AB于于F,M为EF中点,则AM的最小值是.
15. 如图,在Rt中,为边BC上一个动点不与B、C重合),PE⊥AB于于F,M为EF中点,则AM的最小值是.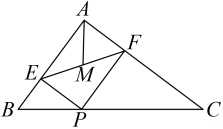 16. 如图,在平面直角坐标系中,所有正方形的中心均在坐标原点,且各边与轴或轴平行,从内到外,它们的边长依次为 , 顶点依次用表示,则顶点的坐标为.
16. 如图,在平面直角坐标系中,所有正方形的中心均在坐标原点,且各边与轴或轴平行,从内到外,它们的边长依次为 , 顶点依次用表示,则顶点的坐标为.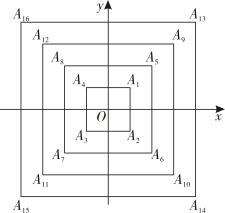
三、解答题(本大题共8小题,共72分.请在答题卡上对应区域作答.)
-
17. 计算:(1)、(2)、已知 , 求的值.18. 已知y与x+1成正比例,且x=-2时y=4,(1)、求与之间的函数关系式;(2)、设点在这个函数的图象上,求.19. 如图所示,汉江是长江最大的支流,它流经美丽的荆门,汉江一侧有一村庄 , 江边原有两个观景台A,B,其中 , 现建设美丽乡村,决定在汉江边新建一个观景台(点A,H,B在同一条直线上),并新修一条路CH,测得千米,千米,千米.
 (1)、CH是不是从村庄到江边的最短路线?请通过计算加以说明;(2)、求原来的路线AC的长.20. 荆门市争创全国文明典范城市,某校举行了创文明城市知识竞赛,全校1800名学生都参加了此次大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
(1)、CH是不是从村庄到江边的最短路线?请通过计算加以说明;(2)、求原来的路线AC的长.20. 荆门市争创全国文明典范城市,某校举行了创文明城市知识竞赛,全校1800名学生都参加了此次大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩作为样本进行整理,得到下列不完整的统计图表: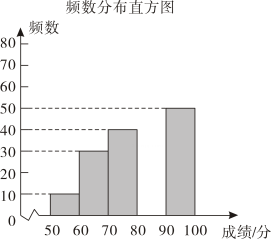
成绩x/分
频数
10
30
40
m
50
频率
0.05
0.15
n
0.35
0.25
(1)、;;(2)、请补全频数分布直方图;(3)、若成绩在90分以上(包括90分)的为“优”等,估计该校参加这次比赛的1800名学生中成绩“优”等约有多少人?21. 如图,在平面直角坐标系xOy中,正比例函数的图象与一次函数的图象的交点坐标为.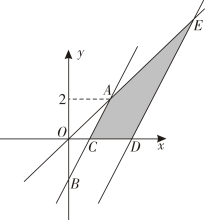 (1)、求和的值;(2)、设一次函数的图象与轴,轴交于B,C两点,将一次函数的图象向右平移2个单位,交图象于点,交轴于点,求四边形ACDE的面积;(3)、直接写出使函数y=kx-k的值小于函数的值的自量的取值范围.22. 如图,在中,对角线AC、BD相交于点 , 过点作 , 交CB延长线于点 , 过点作 , 交AD延长线于点.
(1)、求和的值;(2)、设一次函数的图象与轴,轴交于B,C两点,将一次函数的图象向右平移2个单位,交图象于点,交轴于点,求四边形ACDE的面积;(3)、直接写出使函数y=kx-k的值小于函数的值的自量的取值范围.22. 如图,在中,对角线AC、BD相交于点 , 过点作 , 交CB延长线于点 , 过点作 , 交AD延长线于点. (1)、求证:四边形AECF是矩形;(2)、连接OE,若 , 求的周长.23. 为了落实“乡村振兴”政策,A,B两城决定向C,D两乡运送水泥建设美丽乡村,已知A,B两城分别有水泥200吨和300吨,从城往C,D两乡运送水泥的费用分别为20元/吨和25元/吨;从B城往C,D两乡运送水泥的费用分别为15元/吨和24元/吨,现C乡需要水泥240吨,D乡需要水泥260吨.(1)、设从城运往乡的水泥吨.设总运费为元,写出与的函数关系式并求出最少总运费.(2)、为了更好地支援乡村建设,城运往乡的运费每吨减少元,这时城运往乡的水泥多少吨时总运费最少?24. 如图1,已知一次函数的图象与轴,轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD.
(1)、求证:四边形AECF是矩形;(2)、连接OE,若 , 求的周长.23. 为了落实“乡村振兴”政策,A,B两城决定向C,D两乡运送水泥建设美丽乡村,已知A,B两城分别有水泥200吨和300吨,从城往C,D两乡运送水泥的费用分别为20元/吨和25元/吨;从B城往C,D两乡运送水泥的费用分别为15元/吨和24元/吨,现C乡需要水泥240吨,D乡需要水泥260吨.(1)、设从城运往乡的水泥吨.设总运费为元,写出与的函数关系式并求出最少总运费.(2)、为了更好地支援乡村建设,城运往乡的运费每吨减少元,这时城运往乡的水泥多少吨时总运费最少?24. 如图1,已知一次函数的图象与轴,轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD.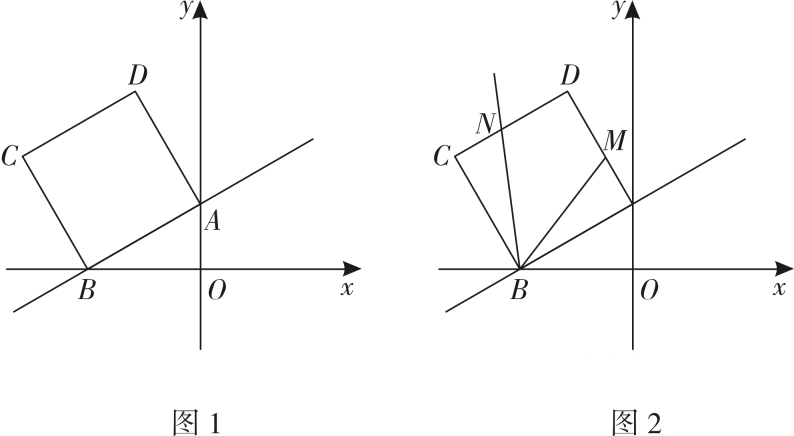 (1)、求边AB的长;(2)、求点C,D的坐标;(3)、作直线BD,将绕点B逆时针旋转,两边分别交正方形的边AD,DC于点M,N(如图2),若M恰为AD的中点,请求出点的坐标.
(1)、求边AB的长;(2)、求点C,D的坐标;(3)、作直线BD,将绕点B逆时针旋转,两边分别交正方形的边AD,DC于点M,N(如图2),若M恰为AD的中点,请求出点的坐标.