广东省深圳市福田区红岭教育集团2023-2024学年九年级上册数学开学试卷
试卷更新日期:2023-09-21 类型:开学考试
一、选择题(每题3分,共30分)
-
1. 下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列等式从左到右的变形,是因式分解的是( )A、x2-4x+4=x(x-4)+4 B、(x+1)2=x2+2x+1 C、x2-4=(x+2)(x-2) D、15x5=3x2•5x33. 用配方法解方程x2-4x-10=0,下列配方结果正确的是( )A、(x+2)2=14 B、(x+2)2=6 C、(x-2)2=14 D、(x-2)2=64. 一元二次方程-x2+2x-1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 一次函数y1=kx+b和y2=2x的图象如图所示,则kx+b≥2x的解集是( )
2. 下列等式从左到右的变形,是因式分解的是( )A、x2-4x+4=x(x-4)+4 B、(x+1)2=x2+2x+1 C、x2-4=(x+2)(x-2) D、15x5=3x2•5x33. 用配方法解方程x2-4x-10=0,下列配方结果正确的是( )A、(x+2)2=14 B、(x+2)2=6 C、(x-2)2=14 D、(x-2)2=64. 一元二次方程-x2+2x-1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 一次函数y1=kx+b和y2=2x的图象如图所示,则kx+b≥2x的解集是( ) A、x≥1 B、x≤2 C、x<1 D、x≤16. 下列命题是真命题的是( )A、若a>b , 则1-2a>1-2b B、等腰三角形的角平分线、中线和高重合 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、一个正多边形的内角和为720°,则这个正多边形的一个外角等于60°7. 某商店需要购进甲乙两种商品,已知甲的进价比乙多50元,分别用2万元进货甲乙两种商品,购买乙的件数比甲多20件,现设乙的进价为x元,则下列方程正确的是( )A、 B、 C、 D、8. 如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形AB边上的高CE的长是( )
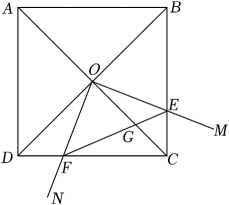
A、x≥1 B、x≤2 C、x<1 D、x≤16. 下列命题是真命题的是( )A、若a>b , 则1-2a>1-2b B、等腰三角形的角平分线、中线和高重合 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、一个正多边形的内角和为720°,则这个正多边形的一个外角等于60°7. 某商店需要购进甲乙两种商品,已知甲的进价比乙多50元,分别用2万元进货甲乙两种商品,购买乙的件数比甲多20件,现设乙的进价为x元,则下列方程正确的是( )A、 B、 C、 D、8. 如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形AB边上的高CE的长是( )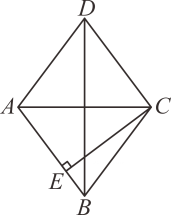 A、4.8cm B、9.6cm C、5cm D、10cm9. 已知关于x的分式方程=4的解为非负数,则a的取值范围是( )A、a≥-4 B、a>-4 C、a≥-4且a≠-1 D、a>-4且a≠-110. 如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;
A、4.8cm B、9.6cm C、5cm D、10cm9. 已知关于x的分式方程=4的解为非负数,则a的取值范围是( )A、a≥-4 B、a>-4 C、a≥-4且a≠-1 D、a>-4且a≠-110. 如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△EOF≌△BOC;③DF2+BE2=2OE2;④正方形ABCD面积是四边形CEOF的面积为的4倍.其中正确的是( )
 A、①②③ B、①③④ C、①②④ D、①②③④
A、①②③ B、①③④ C、①②④ D、①②③④二、填空题(每题3分,共15分)
-
11. 因式分解:2x3-18x= .12. 已知方程2x2-mx+3=0的一个根是-1,则m的值是 .13. 若关于x的分式方程 有增根,则a的值为14. 如图,在周长为32的平行四边形ABCD中,AC、BD交于点O , OE⊥BD交AD于点E , 则△ABE的周长为 .
 15. 如图,在菱形ABCD中,∠B=45°,E、F分别是边CD,BC上的动点,连接AE、EF,G、H分别为AE、EF的中点,连接GH.若GH的最小值为3,则BC的长为 .
15. 如图,在菱形ABCD中,∠B=45°,E、F分别是边CD,BC上的动点,连接AE、EF,G、H分别为AE、EF的中点,连接GH.若GH的最小值为3,则BC的长为 .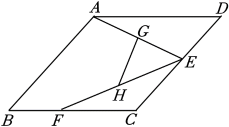
三、解答题(共55分)
-
16. 解方程:(1)、(x-1)2=3(x-1);(2)、x2-4x+1=0.17.(1)、解不等式组:并把它的解集在数轴上表示出来.
 (2)、先化简,再求值: , 其中a=-2.18. 如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(2)、先化简,再求值: , 其中a=-2.18. 如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上. (1)、将△ABC向右平移6个单位长度得到△A1B1C1 , 请画出△A1B1C1;(2)、画出△A1B1C1关于点O的中心对称图形△A2B2C2;(3)、若将△ABC绕某一点旋转可得到△A2B2C2 , 旋转中心的坐标为 .19. 如图,在四边形ABCD中,AB∥DC , AB=AD , 对角线AC , BD交于点O , AC平分∠BAD , 过点C作CE⊥AB , 交AB的延长线于点E , 连接OE .
(1)、将△ABC向右平移6个单位长度得到△A1B1C1 , 请画出△A1B1C1;(2)、画出△A1B1C1关于点O的中心对称图形△A2B2C2;(3)、若将△ABC绕某一点旋转可得到△A2B2C2 , 旋转中心的坐标为 .19. 如图,在四边形ABCD中,AB∥DC , AB=AD , 对角线AC , BD交于点O , AC平分∠BAD , 过点C作CE⊥AB , 交AB的延长线于点E , 连接OE . (1)、求证:四边形ABCD是菱形.(2)、若AB=5,BD=6,求OE的长.20. 某服装店老板用4000元购进了一批甲款恤,用8800元购进了一批乙款恤,已知所购乙款恤数量是甲款恤数量的2倍,购进的乙款恤单价比甲款恤单价贵5元.(1)、购进甲、乙两款恤的单价分别是多少元?(2)、老板把这两种恤的标价都定为每件100元,甲款恤打九折销售,乙款恤按标价销售.经过一段时间的销售,老板发现,销售两种恤共100件时,利润不低于4200元.那么这段时间按标价销售的乙款恤至少要销售多少件?21. 【问题情境】:如图1,点E为正方形ABCD内一点,AE=2,BE=4,∠AEB=90°,将直角三角形ABE绕点A逆时针方向旋转α度(0≤α≤180°)点B、E的对应点分别为点B′、E′.
(1)、求证:四边形ABCD是菱形.(2)、若AB=5,BD=6,求OE的长.20. 某服装店老板用4000元购进了一批甲款恤,用8800元购进了一批乙款恤,已知所购乙款恤数量是甲款恤数量的2倍,购进的乙款恤单价比甲款恤单价贵5元.(1)、购进甲、乙两款恤的单价分别是多少元?(2)、老板把这两种恤的标价都定为每件100元,甲款恤打九折销售,乙款恤按标价销售.经过一段时间的销售,老板发现,销售两种恤共100件时,利润不低于4200元.那么这段时间按标价销售的乙款恤至少要销售多少件?21. 【问题情境】:如图1,点E为正方形ABCD内一点,AE=2,BE=4,∠AEB=90°,将直角三角形ABE绕点A逆时针方向旋转α度(0≤α≤180°)点B、E的对应点分别为点B′、E′.
【问题解决】:
(1)、如图2,在旋转的过程中,点B′落在了AC上,求此时CB′的长;(2)、若α=90°,如图3,得到△ADE′(此时B′与D重合),延长BE交B′E′于点F ,①试判断四边形AEFE′的形状,并说明理由;
②连接CE , 求CE的长;
(3)、在直角三角形ABE绕点A逆时针方向旋转过程中,直接写出线段CE′长度的取值范围.22. 问题提出 (1)、如图①,在△ABC中,D、E分别是AB和AC的中点,连接DE , 则DE与BC的数量关系是 , 位置关系是;(2)、问题探究
(1)、如图①,在△ABC中,D、E分别是AB和AC的中点,连接DE , 则DE与BC的数量关系是 , 位置关系是;(2)、问题探究如图②,在四边形ABCD中,∠BAC=90°,AB=AC=4 , CD=4,E为AD中点,连接BE , 求BE的最大值;
(3)、问题解决如图③,某小区计划在一片足够大的空地上修建四边形的花园ABCD , 其中BC=20米,AD=CD , AD⊥CD , AB∥CD , 由于受地理位置的影响,∠ABC<90°.根据要求,现计划给该花园修建条笔直的绿色长廊,且绿色长廊的入口O定为BC的中点,出口定为点D , 为了尽可能地提高观赏体验,要求绿色长廊OD最长,试求绿色长廊OD最长为多少米?