河南省郑州市管城外国语2023-2024学年八年级上册数学入学考试试卷

试卷更新日期：2023-09-21 类型：开学考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 计算2^-³的结果是（）

A、 $- \frac{1}{8}$ B、 $\frac{1}{8}$ C、–8 D、8

查看试题解析
2. 已知△ABC的三边分别是a、b、c，下列条件中不能判断△ABC为直角三角形的是（）

A、a²+b²=c² B、∠A：∠B：∠C=3：4：5 C、∠A=∠C-∠B D、a=1，b=2，c= $\sqrt{5}$

查看试题解析
3. 下列说法中，正确的是（）

A、2是2的平方根之一 B、2是4的算术平方根 C、3的平方根是3的算术平方根 D、-2的平方是2

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{2} + 2 = 2 \sqrt{2}$ B、 $4 \sqrt{3} - \sqrt{3} = 4$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{24} \div \sqrt{6} = 4$

查看试题解析
5. 已知直角三角形的斜边长为10，两直角边的比为3∶4，则较短直角边的长为（）

A、3 B、6 C、8 D、5

查看试题解析
6. 在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是（　　）

A、 $\frac{36}{5}$ B、 $\frac{12}{5}$ C、9 D、6

查看试题解析
7. 如图，五个正方形放在直线MN上，正方形A、C、E的面积依次为3、5、4，则正方形D的面积之和为（）

A、11 B、14 C、17 D、20

查看试题解析
8. 如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度x(罐壁厚度和小圆孔大小忽略不计)范围是（）

A、12≤x≤13 B、12≤x≤15 C、5≤x≤12 D、5≤x≤13

查看试题解析
9. 等腰三角形一腰长为5，这一腰上的高为3，则这个等腰三角形底边长为（）

A、 $\sqrt{10}$ B、 $3 \sqrt{10}$ C、 $3 \sqrt{10}$ 或 $\sqrt{10}$ D、4或 $3 \sqrt{10}$

查看试题解析
10. 如图，在Rt△ABC中，∠B=90°，以AC为直径的圆恰好过点B.若AB=8，BC=6，则阴影部分的面积是（）

A、100π-24 B、100π-48 C、25π-24 D、25π-48

查看试题解析

二、填空题(每小题3分，共15分)

11. 某种花粉的直径是0.000023毫米，数据0.000023用科学记数法表示为.

查看试题解析
12. $\sqrt{81}$ 的平方根是．

查看试题解析
13. 一个直角三角形的两边长分别为1和2，则第三边长为.

查看试题解析
14. 如图，一圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程(π取3)是.

查看试题解析
15. 如图，由图中的信息可知点P表示的数是.

查看试题解析

三、解答题(本大题共8个小题，共75分)

16.

(1)、 ${(- \sqrt{6})}^{2} - \sqrt{25} + \sqrt{{(- 3)}^{2}} ；$

(2)、 $| - 3 | - {(\frac{1}{3})}^{- 2} + {(π - 3.14)}^{0} + {(- 1)}^{2023}$

查看试题解析
17. 如图：正方形网格中每个小方格的边长为1，且点A、B、C均为格点．

(1)、求△A $BC$ 的面积．

(2)、通过计算判断 $△ ABC$ 的形状．

查看试题解析
18. 地表以下岩层的温度/℃与所处深度/km有如下关系：

深度/km

1

2

3

4

5

温度/℃

55

90

125

160

195

(1)、上表中自变量x是，因变量y是.

(2)、请写出y与x的关系式.

(3)、根据(2)中的关系式，估计地表以下7km处岩层的温度.

查看试题解析
19. 如图，∠ABC=90°，AB=6cm，AD=24cm，BC+CD=34cm，其中点C是直线l上的一个动点，当点C在离点B多远处时，△ACD是以DC为斜边的直角三角形?

查看试题解析
20. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，随板一尺离地，送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千静止的时候，踏板离地高一尺，将它往前推进两步(两步=10尺)，此时踏板升高离地五尺，求秋千绳索的长度.

查看试题解析
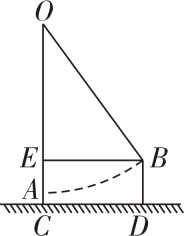21. 阅读下面问题：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1 ； \frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2} ；$

$\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{1 \times (\sqrt{4} - \sqrt{3})}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3} ；$

试求：

(1)、 $\frac{1}{\sqrt{7} + \sqrt{6}} =$

(2)、当n为正整数时， $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ；

(3)、求 $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}}$ 的值.

查看试题解析
22. 如图，长方体的长BE=15cm，宽AB=10cm，高AD=20cm，点M在CH上.且CM=5cm

(1)、求线段DM的长

(2)、一只蚂蚁如果耍沿着长方体的表面从点A爬到点M，需要爬行的最短距离是多少?

查看试题解析
23. 公元3世纪初，我国学家赵爽证明勾定理的图形称为“弦图”.1876年类国总统Garfeild用图1(点C、点B、点C'三点共线)进行了勾股定理的证明.△ACB与△BC'B'是一样的直角三角板，两直角边长为a，b，斜边是c.

(1)、请用此图1证明勾股定理.

(2)、扩展应用1：
如图2，以△ABC的边AB和边AC为边长分别向外作正方形ABFH和正方形CED，过点F、E分别作BC的垂线段FM、EN，那么FM、EN、BC的数量关系是怎样?：说明理由.

(3)、扩展应用2：
如图3，在两平行线m、n之间有一正方形ABCD，已知点A和点C分别在直m、n上，过点D作直线l∥n∥m，已知l、n之间距离为l，l、m之间距离为2.直接出正方形的面积是.

查看试题解析

深度/km	1	2	3	4	5
温度/℃	55	90	125	160	195