福建省福州十一中2023-2024学年九年级上册数学开学试卷
试卷更新日期:2023-09-21 类型:开学考试
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列二次根式中是最简二次根式的是( ).A、 B、 C、 D、2. 如图,在中,点D,E分别为的中点,若 , 则的长度为( )
 A、1 B、2 C、3 D、43. 用配方法解一元二次方程 时,此方程可变形为( )A、 B、 C、 D、4. 在方差计算公式:中, , 分别表示( )A、数据的个数和方差 B、平均数和数据的个数 C、数据的个数和平均数 D、数据的方差和平均数5. 下面哪个点不在函数的图象上( )A、 B、 C、 D、6. 某校在“学习二十大精神”演讲比赛活动中,位评委给某位选手的评分各不相同,去掉个最高分和个最低分,剩下的个评分与原始的个评分相比一定不发生变化的是( )A、平均数 B、中位数 C、方差 D、众数7. 如图,△ABC的中线BD、CE交于点O,连接OA,点G,F分别为OC,OB的中点,BC=4,AO=3,则四边形DEFG的周长为( )
A、1 B、2 C、3 D、43. 用配方法解一元二次方程 时,此方程可变形为( )A、 B、 C、 D、4. 在方差计算公式:中, , 分别表示( )A、数据的个数和方差 B、平均数和数据的个数 C、数据的个数和平均数 D、数据的方差和平均数5. 下面哪个点不在函数的图象上( )A、 B、 C、 D、6. 某校在“学习二十大精神”演讲比赛活动中,位评委给某位选手的评分各不相同,去掉个最高分和个最低分,剩下的个评分与原始的个评分相比一定不发生变化的是( )A、平均数 B、中位数 C、方差 D、众数7. 如图,△ABC的中线BD、CE交于点O,连接OA,点G,F分别为OC,OB的中点,BC=4,AO=3,则四边形DEFG的周长为( )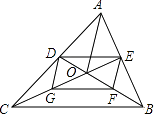 A、6 B、7 C、8 D、128. 如图,抛物线与轴交于点 , 顶点坐标为 , 与轴的交点在、之间不包含端点 , 则的取值范围是( )
A、6 B、7 C、8 D、128. 如图,抛物线与轴交于点 , 顶点坐标为 , 与轴的交点在、之间不包含端点 , 则的取值范围是( ) A、 B、 C、 D、9. 小带和小路两个人开车从城出发匀速行驶至城整个行驶过程中,小带和小路两人的车离开城的距离千米与行驶的时间小时之间的函数关系如图所示,有下列结论:
A、 B、 C、 D、9. 小带和小路两个人开车从城出发匀速行驶至城整个行驶过程中,小带和小路两人的车离开城的距离千米与行驶的时间小时之间的函数关系如图所示,有下列结论:
、两城相距千米;
小路的车比小带的车晚出发小时,却早到小时;
小路的车出发后小时追上小带的车;
当时,小带和小路的车相距千米.
其中正确的结论有( )
A、 B、 C、 D、10. 已知、是一元二次方程的两个不相等的实数根,、是一元二次方程的两个不相等的实数根,其中若 , 则的值为( )A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
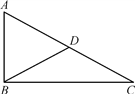
11. 已知是方程的一个根,则 .12. 如图,已知△ABC中,AB=5 cm,BC=12 cm,AC=13 cm,那么AC边上的中线BD的长为cm.
 13. 若函数是正比例函数,则的值为 .14. 若直线和直线的交点坐标为 , 则 .15. 在学校的卫生检查中,规定各班的教室卫生成绩占30%,环境卫生成绩占40%,个人卫生成绩占30%.八年级一班这三项成绩分别为85分,90分和95分,求该班卫生检查的总成绩 .16. 已知抛物线经过 , 两点,若 , 分别位于抛物线对称轴的两侧,且 , 则的取值范围是 .
13. 若函数是正比例函数,则的值为 .14. 若直线和直线的交点坐标为 , 则 .15. 在学校的卫生检查中,规定各班的教室卫生成绩占30%,环境卫生成绩占40%,个人卫生成绩占30%.八年级一班这三项成绩分别为85分,90分和95分,求该班卫生检查的总成绩 .16. 已知抛物线经过 , 两点,若 , 分别位于抛物线对称轴的两侧,且 , 则的取值范围是 .三、计算题(本大题共1小题,共6.0分)
-
17. 解方程: .
四、解答题(本大题共8小题,共80.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 已知:关于的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程两个根均为整数,且为正整数,求的值.19. 已知一次函数的图象过点与 .(1)、求这个一次函数的解析式;(2)、直接写出这个一次函数的图象与两坐标轴的交点坐标.20. 列方程或方程组解应用题:
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了 , 另一边减少了 , 剩余一块面积为的矩形空地空白处 , 求原正方形空地的边长.
 21. 如图,在▱中, , 过点作交的延长线于点 , 连接交于点 .
21. 如图,在▱中, , 过点作交的延长线于点 , 连接交于点 . (1)、求证:四边形是矩形;(2)、在▱中,取的中点 , 连接 , 若 , 且 , 求四边形的面积.22. 2017年月在北京市召开的第十二届全国人民代表大会第五次会议上,环境问题再次成为大家讨论的重点内容之一.年月日是世界环境日,为纪念第个世界环境日,某中学举行了一次“环保知识竞赛”,共有名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了名学生的成绩进行统计分析,经分组整理后绘制成频数分布表和频数分布直方图.
(1)、求证:四边形是矩形;(2)、在▱中,取的中点 , 连接 , 若 , 且 , 求四边形的面积.22. 2017年月在北京市召开的第十二届全国人民代表大会第五次会议上,环境问题再次成为大家讨论的重点内容之一.年月日是世界环境日,为纪念第个世界环境日,某中学举行了一次“环保知识竞赛”,共有名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了名学生的成绩进行统计分析,经分组整理后绘制成频数分布表和频数分布直方图.频数分布表
分组分
频数
频率
合计
 (1)、请你根据图表提供的信息,解答下列问题: , , ;(2)、请补全频数分布直方图;(3)、若成绩在分以上含分为优秀,则该校成绩优秀的约为人.23. 在矩形中,是边上一点.
(1)、请你根据图表提供的信息,解答下列问题: , , ;(2)、请补全频数分布直方图;(3)、若成绩在分以上含分为优秀,则该校成绩优秀的约为人.23. 在矩形中,是边上一点. (1)、求作点 , 使得 , 关于直线对称要求:尺规作图,不写作法,保留作图痕迹;(2)、平移线段 , 使点与点重合,点的对应点为求证点落在线段上.
(1)、求作点 , 使得 , 关于直线对称要求:尺规作图,不写作法,保留作图痕迹;(2)、平移线段 , 使点与点重合,点的对应点为求证点落在线段上.
-
