青海省2023年中考数学试卷
试卷更新日期:2023-09-21 类型:中考真卷
一、单选题
-
1. 青海地大物博,风光秀美,素有“大美青海”之美誉.下面四个艺术字中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 计算的结果是( )A、1 B、 C、5 D、3. 如图,直线 , 相交于点O , , 则的度数是( )
2. 计算的结果是( )A、1 B、 C、5 D、3. 如图,直线 , 相交于点O , , 则的度数是( )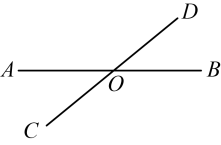 A、 B、 C、 D、4. 下列几何体中,其主视图、左视图和俯视图完全相同的是( )A、
A、 B、 C、 D、4. 下列几何体中,其主视图、左视图和俯视图完全相同的是( )A、 B、
B、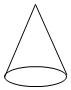 C、
C、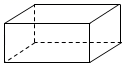 D、
D、 5. 下列运算正确的是( )A、 B、 C、 D、6. 为了缅怀革命先烈,传承红色精神,青海省某学校八年级师生在清明节期间前往距离学校的烈士陵园扫墓.一部分师生骑自行车先走,过了后,其余师生乘汽车出发,结果他们同时到达;已知汽车的速度是骑车师生速度的2倍,设骑车师生的速度为.根据题意,下列方程正确的是( )A、 B、 C、 D、7. 如图,是的弦,C是上一点, , 垂足为D , 若 , 则( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 为了缅怀革命先烈,传承红色精神,青海省某学校八年级师生在清明节期间前往距离学校的烈士陵园扫墓.一部分师生骑自行车先走,过了后,其余师生乘汽车出发,结果他们同时到达;已知汽车的速度是骑车师生速度的2倍,设骑车师生的速度为.根据题意,下列方程正确的是( )A、 B、 C、 D、7. 如图,是的弦,C是上一点, , 垂足为D , 若 , 则( ) A、 B、 C、 D、8. 生物兴趣小组探究酒精对某种鱼类的心率是否有影响,实验得出心率与酒精浓度的关系如图所示,下列说法正确的是( )
A、 B、 C、 D、8. 生物兴趣小组探究酒精对某种鱼类的心率是否有影响,实验得出心率与酒精浓度的关系如图所示,下列说法正确的是( ) A、酒精浓度越大,心率越高 B、酒精对这种鱼类的心率没有影响 C、当酒精浓度是时,心率是168次/分 D、心率与酒精浓度是反比例函数关系
A、酒精浓度越大,心率越高 B、酒精对这种鱼类的心率没有影响 C、当酒精浓度是时,心率是168次/分 D、心率与酒精浓度是反比例函数关系二、填空题
-
9. ﹣ 的绝对值是 .10. 写出一个比 大且比 小的整数 .11. 青藏联网工程东起青海西宁,西至西藏拉萨,被誉为“电力天路”.截至2023年5月“电力天路”已安全运行近12年,累计向西藏送电亿千瓦时,数据亿用科学记数法表示为.12. 在平面直角坐标系中,点P(-1,2)向右平移3个单位长度得到的点的坐标是 .13. 如图,是的切线,是切点,连接 , . 若 , 则的度数是 .
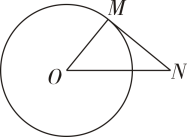 14. 如图,正方形ABCD的边长是4,分别以点A , B , C , D为圆心,2为半径作圆,则图中阴影部分的面积是(结果保留).
14. 如图,正方形ABCD的边长是4,分别以点A , B , C , D为圆心,2为半径作圆,则图中阴影部分的面积是(结果保留).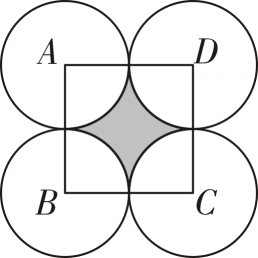 15. 如图,在中,是的垂直平分线.若 , , 则的周长是.
15. 如图,在中,是的垂直平分线.若 , , 则的周长是.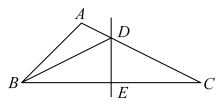 16. 如图是平面直角坐标系中的一组直线,按此规律推断,第5条直线与x轴交点的横坐标是.
16. 如图是平面直角坐标系中的一组直线,按此规律推断,第5条直线与x轴交点的横坐标是.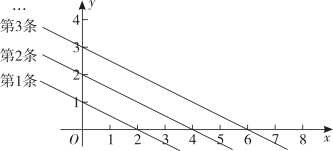
三、解答题
-
17. 计算: .18. 先化简,再求值: , 其中 .19. 在同一平面直角坐标系中,一次函数和反比例函数的图象如图所示.
 (1)、求一次函数的解析式;(2)、当时,直接写出不等式的解集.20. 为丰富学生课余生活,提高学生运算能力,数学小组设计了如下的解题接力游戏:(1)、解不等式组:;(2)、当m取(1)的一个整数解时,解方程.21. 如图,是的一个外角, , .
(1)、求一次函数的解析式;(2)、当时,直接写出不等式的解集.20. 为丰富学生课余生活,提高学生运算能力,数学小组设计了如下的解题接力游戏:(1)、解不等式组:;(2)、当m取(1)的一个整数解时,解方程.21. 如图,是的一个外角, , . (1)、尺规作图:作的平分线,交于点D(保留作图痕迹,不写作法);(2)、求证:四边形是平行四边形.22. 为了方便观测动物的活动情况,某湿地公园要铺设一段道路.计划从图中 , 两处分别向处铺设,现测得 , , , 求 , 两点间的距离.(结果取整数,参考数据: , , )
(1)、尺规作图:作的平分线,交于点D(保留作图痕迹,不写作法);(2)、求证:四边形是平行四边形.22. 为了方便观测动物的活动情况,某湿地公园要铺设一段道路.计划从图中 , 两处分别向处铺设,现测得 , , , 求 , 两点间的距离.(结果取整数,参考数据: , , ) 23. 为更好引导和促进旅游业恢复发展,深入推动大众旅游,文化和旅游部决定开展2023年“5·19中国旅游日”活动.青海省某旅行社为了解游客喜爱的旅游景区的情况,对“五一”假期期间的游客去向进行了随机抽样调查,并绘制如下不完整的统计图,请根据图1,图2中所给的信息,解答下列问题:
23. 为更好引导和促进旅游业恢复发展,深入推动大众旅游,文化和旅游部决定开展2023年“5·19中国旅游日”活动.青海省某旅行社为了解游客喜爱的旅游景区的情况,对“五一”假期期间的游客去向进行了随机抽样调查,并绘制如下不完整的统计图,请根据图1,图2中所给的信息,解答下列问题: (1)、此次抽样调查的样本容量是;(2)、将图1中的条形统计图补充完整;(3)、根据抽样调查结果,“五一”假期期间这四个景区共接待游客约19万人,请估计前往青海湖景区的游客约有多少万人;(4)、若甲、乙两名游客从四个景区中任选一个景区旅游,请用树状图或列表法求出他们选择同一景区的概率.24. 如图,二次函数的图象与轴相交于点和点 , 交轴于点 .
(1)、此次抽样调查的样本容量是;(2)、将图1中的条形统计图补充完整;(3)、根据抽样调查结果,“五一”假期期间这四个景区共接待游客约19万人,请估计前往青海湖景区的游客约有多少万人;(4)、若甲、乙两名游客从四个景区中任选一个景区旅游,请用树状图或列表法求出他们选择同一景区的概率.24. 如图,二次函数的图象与轴相交于点和点 , 交轴于点 . (1)、求此二次函数的解析式;(2)、设二次函数图象的顶点为 , 对称轴与轴交于点 , 求四边形的面积(请在图1中探索);(3)、二次函数图象的对称轴上是否存在点 , 使得是以为底边的等腰三角形?若存在,请求出满足条件的点的坐标;若不存在,请说明理由(请在图中探索).25. 综合与实践
(1)、求此二次函数的解析式;(2)、设二次函数图象的顶点为 , 对称轴与轴交于点 , 求四边形的面积(请在图1中探索);(3)、二次函数图象的对称轴上是否存在点 , 使得是以为底边的等腰三角形?若存在,请求出满足条件的点的坐标;若不存在,请说明理由(请在图中探索).25. 综合与实践车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆,车轮都是圆形的.为什么车轮要做成圆形的呢?这里面有什么数学道理吗?带着这样的疑问,小青做了如下的探究活动:
将车轮设计成不同的正多边形,在水平地面上模拟行驶.
 (1)、探究一:将车轮设计成等边三角形,转动过程如图1,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图2中计算C到的距离.(2)、探究二:将车轮设计成正方形,转动过程如图3,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图4中计算C到的距离(结果保留根号).(3)、探究三:将车轮设计成正六边形,转动过程如图5,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),在图6中计算C到的距离(结果保留根号).(4)、归纳推理:比较 , , 大小: , 按此规律推理,车轮设计成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线(水平线)的距离(填“越大”或“越小”).(5)、得出结论:将车轮设计成圆形,转动过程如图7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)的距离.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.
(1)、探究一:将车轮设计成等边三角形,转动过程如图1,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图2中计算C到的距离.(2)、探究二:将车轮设计成正方形,转动过程如图3,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图4中计算C到的距离(结果保留根号).(3)、探究三:将车轮设计成正六边形,转动过程如图5,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),在图6中计算C到的距离(结果保留根号).(4)、归纳推理:比较 , , 大小: , 按此规律推理,车轮设计成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线(水平线)的距离(填“越大”或“越小”).(5)、得出结论:将车轮设计成圆形,转动过程如图7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)的距离.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.