广西柳州十五中2023-2024学年八年级上册数学开学试卷
试卷更新日期:2023-09-21 类型:开学考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下面所给的交通标志图中是轴对称图形的是A、
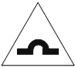 B、
B、 C、
C、 D、
D、 2. 根据下列表述,不能确定一点的具体位置的是( )A、东经 , 北纬 B、礼堂排号 C、重庆市宏帆路 D、港口南偏东方向上距港口海里3. 下列命题中正确的是( )A、在同一平面内,过一点有且只有一条直线和已知直线垂直 B、互补的两个角是邻补角 C、在同一平面内,如果 , , 则 D、两直线平行,同旁内角相等4. 数学活动课上,小明想用三根木棒首尾顺次相接制作一个三角形模型,现有两根长度分别为和的木棒,则第三根木棒的长度可取( )A、 B、 C、 D、5. 已知 , 为实数,且 , 则的立方根是( )A、 B、 C、 D、6. 如图,小明在操场上从点出发,沿直线前进米后向左转 , 再沿直线前进米后,又向左转 , 这样走下去,他第一次回到出发地点时,一共走了( )米
2. 根据下列表述,不能确定一点的具体位置的是( )A、东经 , 北纬 B、礼堂排号 C、重庆市宏帆路 D、港口南偏东方向上距港口海里3. 下列命题中正确的是( )A、在同一平面内,过一点有且只有一条直线和已知直线垂直 B、互补的两个角是邻补角 C、在同一平面内,如果 , , 则 D、两直线平行,同旁内角相等4. 数学活动课上,小明想用三根木棒首尾顺次相接制作一个三角形模型,现有两根长度分别为和的木棒,则第三根木棒的长度可取( )A、 B、 C、 D、5. 已知 , 为实数,且 , 则的立方根是( )A、 B、 C、 D、6. 如图,小明在操场上从点出发,沿直线前进米后向左转 , 再沿直线前进米后,又向左转 , 这样走下去,他第一次回到出发地点时,一共走了( )米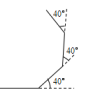 A、 B、 C、 D、7. 如图,在五边形中, , , , 则的度数是( )
A、 B、 C、 D、7. 如图,在五边形中, , , , 则的度数是( ) A、 B、 C、 D、8. 已知是方程组的解,则的值是( )A、 B、 C、 D、9. 如图, , 平分 , , , , 则下列结论:
A、 B、 C、 D、8. 已知是方程组的解,则的值是( )A、 B、 C、 D、9. 如图, , 平分 , , , , 则下列结论:
;平分;; .
其中正确结论的个数是( )
A、个 B、个 C、个 D、个10. 对 , 定义一种新的运算 , 规定 , 若关于正数的不等式组恰好有个整数解,则的取值范围是( )A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
11. 若点在轴上,则 .12. 已知 , , 那么的平方根是 .13. 如图,长方形的长为8,宽为6,将这个长方形向上平移3个单位,再向左平移2个单位,得到长方形 , 则阴影部分的面积为 .
 14. 如图,为的中线,的周长为 , 的周长为 , , 则为 .
14. 如图,为的中线,的周长为 , 的周长为 , , 则为 . 15. 空竹是我国传统的一项游戏,其器材简单但是动作花样繁多,深受大众喜爱彤彤在跑步时发现广场上抖空竹的老奶奶的某个动作可以抽象成一个简单的数学图形,如图所示, , , , 则的度数是 .
15. 空竹是我国传统的一项游戏,其器材简单但是动作花样繁多,深受大众喜爱彤彤在跑步时发现广场上抖空竹的老奶奶的某个动作可以抽象成一个简单的数学图形,如图所示, , , , 则的度数是 . 16. 的两边与的两边分别平行,且是的余角的4倍,则.
16. 的两边与的两边分别平行,且是的余角的4倍,则.三、解答题(本大题共7小题,共52.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算:
.
18. 解不等式组 , 把它的解集在数轴上表示出来,并写出它的整数解.19. 某社区随机抽取了部分家庭,调查他们每月用于“信息消费”的金额单位:元 , 将数据分组如下:A.;B.;C.;D.;E. , 并将数据整理成如图所示的不完整统计图已知、两组户数在频数分布直方图中的高度比为: .
请根据以上信息,解答下列问题:
(1)、组的频数是多少?本次调查的样本容量是多少?(2)、抽取的家庭中每月用于“信息消费”的金额不少于元的有多少户?(3)、求扇形统计图中组所占扇形的圆心角的大小.20. 如图,四边形中, , , 点 , 分别在 , 上,将沿翻折,得 , 若 , , 求的度数. 21. 现在以及未来,会有更多的高科技应用在我们日常的生产生活中,比如:无人机放牧,机器狗导盲,智能化无人码头装卸等某快递公司为了提高工作效率,计划购买 , 两种型号的机器人来搬运货物,已知每台型机器人比每台型机器人每天多搬运吨,并且台型机器人和台型机器人每天共搬运货物吨.(1)、求每台型机器人和每台型机器人每天分别搬运货物多少吨?(2)、每台型机器人售价万元,每台型机器人售价万元,该公司采购 , 两种型号的机器人若干台,费用恰好是万元,求出 , 两种机器人分别采购多少台?22. 如图, , , .
21. 现在以及未来,会有更多的高科技应用在我们日常的生产生活中,比如:无人机放牧,机器狗导盲,智能化无人码头装卸等某快递公司为了提高工作效率,计划购买 , 两种型号的机器人来搬运货物,已知每台型机器人比每台型机器人每天多搬运吨,并且台型机器人和台型机器人每天共搬运货物吨.(1)、求每台型机器人和每台型机器人每天分别搬运货物多少吨?(2)、每台型机器人售价万元,每台型机器人售价万元,该公司采购 , 两种型号的机器人若干台,费用恰好是万元,求出 , 两种机器人分别采购多少台?22. 如图, , , . (1)、求证:;(2)、求证: .23. 阅读下面资料:小明遇到这样一个问题:如图 , 对面积为的逐次进行以下操作:分别延长、、至、、 , 使得 , , , 顺次连接、、 , 得到 , 记其面积为 , 求的值.
(1)、求证:;(2)、求证: .23. 阅读下面资料:小明遇到这样一个问题:如图 , 对面积为的逐次进行以下操作:分别延长、、至、、 , 使得 , , , 顺次连接、、 , 得到 , 记其面积为 , 求的值.小明是这样思考和解决这个问题的:如图 , 连接C、A、 , 因为 , , , 根据等高两三角形的面积比等于底之比,所以 , 由此继续推理,从而解决了这个问题.

 (1)、直接写出用含字母的式子表示 .(2)、请参考小明同学思考问题的方法,解决下列问题:
(1)、直接写出用含字母的式子表示 .(2)、请参考小明同学思考问题的方法,解决下列问题:如图 , 为内一点,连接、、并延长分别交边、、于点、、 , 则把分成六个小三角形,其中四个小三角形面积已在图上标明,求的面积.
(3)、如图 , 若点为的边上的中线的中点,求与的比值.