河南省郑州市中牟县重点学校2023-2024学年九年级上册数学开学试卷
试卷更新日期:2023-09-21 类型:开学考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知 , 下列式子不成立的是( )A、 B、 C、 D、3. 若将中的x与y都扩大2倍,则这个代数式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、缩小到原来的4. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
2. 已知 , 下列式子不成立的是( )A、 B、 C、 D、3. 若将中的x与y都扩大2倍,则这个代数式的值( )A、不变 B、扩大2倍 C、扩大4倍 D、缩小到原来的4. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )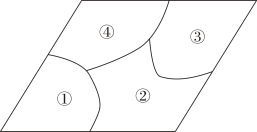 A、 B、 C、 D、5. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分若从这四部著作中(随机抽取两本先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是( )
A、 B、 C、 D、5. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分若从这四部著作中(随机抽取两本先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是( ) A、 B、 C、 D、6. 为扎实推进“五育”并举工作,加强劳动教育,东营市某中学针对七年级学生开设了“跟我学面点”烹饪课程,课程开设后学校花费6000元购进第一批面粉,用完后学校又花费9600元购进了第二批面粉,第二批面粉的采购量是第一批采购量的1.5倍,但每千克面粉价格提高了0.4元.设第一批面粉采购量为x千克,依题意所列方程正确的是( )A、 B、 C、 D、7. 关于x的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根8. 关于的不等式的解集如图所示,则等于( )
A、 B、 C、 D、6. 为扎实推进“五育”并举工作,加强劳动教育,东营市某中学针对七年级学生开设了“跟我学面点”烹饪课程,课程开设后学校花费6000元购进第一批面粉,用完后学校又花费9600元购进了第二批面粉,第二批面粉的采购量是第一批采购量的1.5倍,但每千克面粉价格提高了0.4元.设第一批面粉采购量为x千克,依题意所列方程正确的是( )A、 B、 C、 D、7. 关于x的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根8. 关于的不等式的解集如图所示,则等于( ) A、 B、 C、 D、9. 如图,在中, , , 以为圆心,任意长为半径画弧分别交、于点和 , 再分别以、为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长交于点 , 则下列说法中正确的个数是( )
A、 B、 C、 D、9. 如图,在中, , , 以为圆心,任意长为半径画弧分别交、于点和 , 再分别以、为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长交于点 , 则下列说法中正确的个数是( )
若 , 则点到的距离为;
;
点在的中垂线上;
若 , 则 .
A、个 B、个 C、个 D、个10. 如图,在平面直角坐标系中,四边形的顶点在原点上,边在轴的正半轴上轴, , , , 将四边形绕点逆时针旋转,每次旋转 , 则第次旋转结束时,点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题,共15.0分)
-
11. 请写出一个分式,并写出使其有意义的条件 .12. 如图,在▱中,的平分线交于点 , 的平分线交于点 , 若 , , 则的长是 .
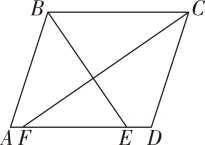 13. 如图,在中, , 分别是和上的点, , , , 且 , 则 .
13. 如图,在中, , 分别是和上的点, , , , 且 , 则 . 14. 如图,已知函数与函数的图象交于点 , 则关于的不等式的解集是 .
14. 如图,已知函数与函数的图象交于点 , 则关于的不等式的解集是 . 15. 如图,等边三角形的边长为 , 动点从点出发,沿的方向以的速度运动,动点从点出发,沿的方向以的速度运动,且动点 , 同时出发,其中一点到达终点时,另一点随之停止运动那么运动到第秒时,点 , , 以及的边上一点恰能构成一个平行四边形.
15. 如图,等边三角形的边长为 , 动点从点出发,沿的方向以的速度运动,动点从点出发,沿的方向以的速度运动,且动点 , 同时出发,其中一点到达终点时,另一点随之停止运动那么运动到第秒时,点 , , 以及的边上一点恰能构成一个平行四边形.
三、解答题(本大题共7小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
-
16.(1)、因式分解:;(2)、解不等式组: .17. 化简 , 下面是甲、乙两同学的部分运算过程:
甲同学:解:原式;
乙同学:解:原式
(1)、甲同学解法的依据是 , 乙同学解法的依据是;填序号等式的基本性质;
分式的基本性质;
乘法分配律;
乘法交换律.
(2)、请从甲、乙同学的解法中选择一种,写出完整的化简过程,然后从 , , , , 中挑选一个合适的数代入求值.18. 如图,在平面直角坐标系中,的顶点 , , 均在正方形网格的格点上.
⑴将沿轴方向向左平移个单位后得到 , 画出;
⑵将绕顺时针旋转后得到 , 画出 , 并写出顶点 , , 的坐标.
19. 如图,中,点D在边AC上,且 . (1)、请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).(2)、若(1)中所作的角平分线与边BC交于点E,连接DE.求证: .20. “双减”政策受到各地教育部门的积极响应,某校为增加学生的课外活动时间,现决定增购两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多3元,用800元购买的跳绳个数和用500元购买的键子数量相同.(1)、求跳绳和毽子的单价分别是多少元?(2)、由于库存较大,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七折出售.学校计划购买跳绳和毽子两种器材共600个,且要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于460根,请你求出学校花钱最少的购买方案.21. 课本再现
(1)、请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).(2)、若(1)中所作的角平分线与边BC交于点E,连接DE.求证: .20. “双减”政策受到各地教育部门的积极响应,某校为增加学生的课外活动时间,现决定增购两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多3元,用800元购买的跳绳个数和用500元购买的键子数量相同.(1)、求跳绳和毽子的单价分别是多少元?(2)、由于库存较大,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七折出售.学校计划购买跳绳和毽子两种器材共600个,且要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于460根,请你求出学校花钱最少的购买方案.21. 课本再现思考
我们知道,菱形的对角线互相垂直,反过来,对角线互相垂直的平行四边形是菱形吗?
可以发现并证明菱形的一个判定定理;
对角线互相垂直的平行四边形是菱形.
定理证明
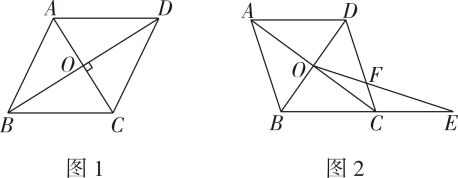
(1)、为了证明该定理,小明同学画出了图形如图 , 并写出了“已知”和“求证”,请你完成证明过程.已知:在▱中,对角线 , 垂足为 .
求证:▱是菱形.
(2)、知识应用如图 , 在▱中,对角线和相交于点 , , , .
求证:▱是菱形.
22. 已知:是等腰三角形,其中 , , 点为边上的任意一点,连接 , 将线段绕点逆时针旋转 , 使点落在点处,连接、 . (1)、当时,如图 , 此时恰好平分 , 则和的数量关系是:;(2)、当时:
(1)、当时,如图 , 此时恰好平分 , 则和的数量关系是:;(2)、当时:请判断线段 , , 的数量关系,并根据图进行证明提示:过点作 , 交与;
若 , 在点的移动过程中,当是等腰三角形时,直接写出此时的面积.