黑龙江省佳木斯二十中2023-2024学年八年级上册数学开学考试试卷

试卷更新日期：2023-09-21 类型：开学考试

进入出卷网下载

一、选择题（每题3分）

1. 平面直角坐标系内AB∥x轴，AB＝1，点A的坐标为（-2，3）（）

A、（-1，4） B、（-1，3） C、（-3，3）或（-1，-2） D、（-1，3）或（-3，3）

查看试题解析
2. 如果a是任意实数，则点P（a-2，a-1）一定不在第（）

A、一 B、二 C、三 D、四

查看试题解析
3. 在同一平面内，两条直线的位置关系可能是（）

A、相交或垂直 B、垂直或平行 C、平行或相交 D、相交或垂直或平行

查看试题解析
4. 不等式组 ${\begin{cases} 2 x - 1 \leq 5 \\ - x + 2 < 3 \end{cases}$ 的解集表示在数轴上为（）

A、 B、 C、 D、

查看试题解析
5. 如图，把长方形ABCD沿EF折叠后，点D ， C'的位置．若∠D'EF＝65°，则∠C′FB是（）

A、45° B、50° C、60° D、65°

查看试题解析
6. 下列说法正确的有（）
①带根号的数都是无理数；

②立方根等于本身的数是0和1；

③-a一定没有平方根；

④实数与数轴上的点是一一对应的；

⑤两个无理数的差还是无理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ 是二元一次方程组 ${\begin{cases} m x + n y = 8 \\ n x - m y = 1 \end{cases}$ 的解，则4n-2m的算术平方根为（　　）

A、2 B、 $\sqrt{2}$ C、±2 D、 $\pm \sqrt{2}$

查看试题解析
8. 已知整数a₁ ， a₂ ， a₃ ， a₄ ， …满足下列条件：a₁＝0，a₂＝-|a₁+1|．a₃＝-|a₂+2|，a₄＝-|a₃+3|，…依此类推，则a₂₀₂₂的值为（）

A、2022 B、-2022 C、-1011 D、1011

查看试题解析
9. 如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，DO＝4，平移距离为6（）

A、24 B、40 C、42 D、48

查看试题解析
10. 如图，CD∥AB，OE平分∠AOD，OF⊥OE，OG⊥CD，∠CDO＝50°，则下列结论：
①∠AOE＝65°；②OF平分∠BOD；③∠GOE＝∠DOF；④∠AOE＝∠GOD.

其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分）

11. 在 $\sqrt{1}$ ， $\sqrt{2}$ ， $\sqrt{3}$ ， … $\sqrt{2006}$ 中，共有个有理数．

查看试题解析
12. 关于x的不等式组 ${\begin{cases} 2 x - 3 \leq 5 \\ - x + a < 2 \end{cases}$ 只有4个整数解，则a的取值范围是．

查看试题解析
13. 到x轴距离为6，到y轴距离为4的坐标为．

查看试题解析
14. 若点P（2-m ， 3m+1）在x轴上，则m＝．

查看试题解析
15. 如果一个多边形的每一个内角都相等，且内角和为1440°，则这个多边形的外角是．

查看试题解析
16. 如图，四边形ABCD中，∠A＝100°，点M、N分别在AB、BC上，将△BMN沿MN翻折，FN∥DC ，则∠B的度数为°．

查看试题解析
17. 若a＞b ，则 $- \frac{7}{5} a$ $- \frac{7}{5} b$ （填“＞”或“＜”）．

查看试题解析
18. 若 $2 x + y = 1$ ，且 $0 < y < 1$ ，则 $x$ 的取值范围为.

查看试题解析
19. 如图，将直角三角形ACB沿射线CB方向平移8cm，得到三角形A′C′B′，BC＝4cm，AC＝5cm，则阴影部分的面积为cm² ．

查看试题解析
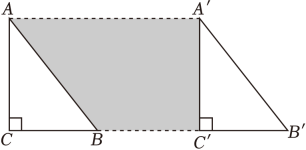20. 如图，在平面直角坐标系中，一动点从原点O出发，每次移动1个单位，依次得到点P₁（0，1），P₂（1，1），P₃（1，0），P₄（1，-1），P₅（2，-1），P₆（2，0）…，则点P₂₀₂₃的坐标是．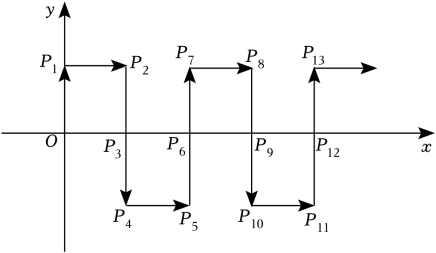

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt[3]{- 27} + \sqrt{{(- 3)}^{2}} + \sqrt[3]{- 1}$ ；

(2)、 $- 1^{2} + \sqrt[3]{64} - (- 2) \times \sqrt{9}$ ．

查看试题解析
22. 如图，方格纸中的每个小正方形都是边长为1个单位长度的正方形，△ABC的顶点都在格点上

(1)、点A的坐标为，点C的坐标为；

(2)、将△ABC先向左平移3个单位长度，再向下平移6个单位长度，请画出平移后的△A₁B₁C₁ ．

查看试题解析

23. 中华文明，源远流长；中华汉字，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理

成绩x/分	频数	频率
50≤x＜60	10	0.05
60≤x＜70	30	0.15
70≤x＜80	40	n
80≤x＜90	m	0.35
90≤x≤100	50	0.25

请根据所给信息，解答下列问题：

(1)、m＝， n＝；

(2)、请补全频数分布直方图；

(3)、若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？

查看试题解析

24. 如图，已知AE∥BF ， ∠A＝60°，点P为射线AE上任意一点（不与点A重合），BC ， BD分别平分∠ABP和∠PBF ，点D ．

(1)、图中∠CBD＝°；

(2)、当∠ACB＝∠ABD时，∠ABC＝°；

(3)、随点P位置的变化，图中∠APB与∠ADB之间的数量关系始终为 ▲ ，请说明理由．

查看试题解析
25. 随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具．某汽车销售公司计划购进一批新能源汽车尝试进行销售；3辆A型汽车、2辆B型汽车的进价共计95万元

(1)、求A、B两种型号的汽车每辆进价分别为多少万元？

(2)、若该公司计划正好用200万元购进以上两种型号的新能源汽车（两种型号的汽车均购买），请你帮助该公司设计购买方案；

(3)、若该汽车销售公司销售1辆A型汽车可获利8000元，销售1辆B型汽车可获利5000元，在（2）中的购买方案中，哪种方案获利最大？最大利润是多少元？

查看试题解析
26. 将下面的证明过程补充完整，括号内写上相应理由或依据：
已知，如图，CD⊥AB ，垂足分别为D、F ， ∠B+∠BDG＝180°

证明：∵CD⊥AB ， EF⊥AB（已知）

∴∠BFE＝∠BDC＝90°（）

∴EF∥    ▲    （）

∴∠BEF＝    ▲    （）

又∵∠B+∠BDG＝180°（已知）

∴BC∥    ▲    （）

∴∠CDG＝    ▲    （）

∴∠CDG＝∠BEF（）

查看试题解析
27. 综合与探究：
如图在平面直角坐标系中，O为原点，已知点A（0，a）（b ， 0）、C（c ， 0），且（a-4）²+ $\sqrt{b + 2}$ +|c-4|＝0，将点B向右平移6个单位长度，得到对应点D ．

(1)、点A的坐标为，点B的坐标为，点C的坐标为；

(2)、求△ACD的面积；

(3)、若点P为x轴上的一个动点，是否存在点P ，使△PAO的面积等于△PAC面积的2倍，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析