辽宁省盘锦二中2023-2024学年九年级上册数学期初试卷
试卷更新日期:2023-09-21 类型:开学考试
一、单项选择题(每小题2分,满分20分)
-
1. 立方根等于本身的数是( )A、1 B、0 C、±1 D、±1.02. -1的平方根说法正确的是( )A、1 B、-1 C、±1 D、没有3. 为了了解某校八年级400名学生的视力情况,从中抽查了60名学生的视力情况,针对这个问题( )A、400名学生是总体 B、每名学生是个体 C、60名学生的视力是所抽取的一个样本 D、60名学生是所抽取的一个样本4. 下列各数中,是无理数的是( )A、 B、3.14 C、 D、05. 点P(3,-4)在第四象限,则点P到x轴的距离是( )A、3 B、4 C、-3 D、-46. 下面四个图形中,线段BE是△ABC的高的图是( )A、
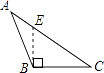 B、
B、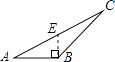 C、
C、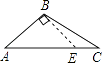 D、
D、 7. 若不等式组的解集为﹣1≤x≤3,则图中表示正确的是( )A、
7. 若不等式组的解集为﹣1≤x≤3,则图中表示正确的是( )A、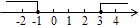 B、
B、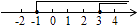 C、
C、 D、
D、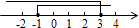 8. 的算术平方根是( )A、5 B、﹣5 C、 D、9. 一个等腰三角形的两边长为8和10,则它的周长m的取值为( )A、26或28 B、26 C、28 D、26<m<2810. 如图,把长方形ABCD沿EF折叠后,点D,C′的位置,若∠DEF=65°,则∠C'FB是( )
8. 的算术平方根是( )A、5 B、﹣5 C、 D、9. 一个等腰三角形的两边长为8和10,则它的周长m的取值为( )A、26或28 B、26 C、28 D、26<m<2810. 如图,把长方形ABCD沿EF折叠后,点D,C′的位置,若∠DEF=65°,则∠C'FB是( )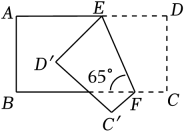 A、45° B、50° C、60° D、65°
A、45° B、50° C、60° D、65°二、填空题(每小题3分,共18分)
-
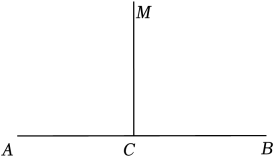
11. 要使有意义,则的范围 .12. 如图,现要从幸福小区M修建一条连接街道AB的最短小路,过点M作MC⊥AB于点C , 这样做的依据是 .
 13. 已知一个40个数据的样本,把它分成六组,第一组到第四组的频数分别为10,5,7,6,第五组的频率是0.10,则第六组的频数为 .14. 如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7= .
13. 已知一个40个数据的样本,把它分成六组,第一组到第四组的频数分别为10,5,7,6,第五组的频率是0.10,则第六组的频数为 .14. 如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7= .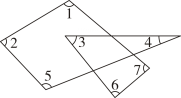 15. 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离为3,则阴影部分的面积为 .
15. 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离为3,则阴影部分的面积为 . 16. 如图,在平面直角坐标系中,一动点沿箭头所示的方向,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),…,则P2023的坐标是 .
16. 如图,在平面直角坐标系中,一动点沿箭头所示的方向,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),…,则P2023的坐标是 .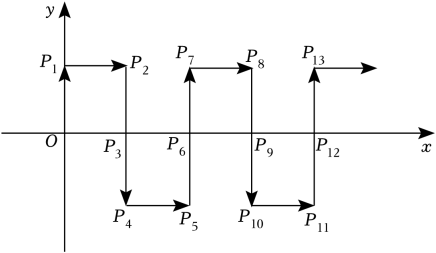
三、解答题(共82分)
-
17.(1)、计算: .(2)、解方程组: .18. 解不等式组: ;并写出它的整数解.19. 一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.20. 如图是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点,点A,B,B的坐标分别为A(1,1),B(4,0),请解答下列问题:
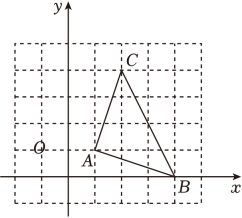
⑴直接写出点C的坐标;
⑵将△ABC先向左平移2个单位长度,再向下平移1个单位长度得到△DEF,(点A,B,C的对应点分别为D,E,F),画出△DEF;
⑶直接写出⑵中四边形DBCF的面积为 ▲ .
21. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式(1)、下列选取样本的方法最合理的一种是 . (只需填上正确答案的序号)①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
(2)、本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图: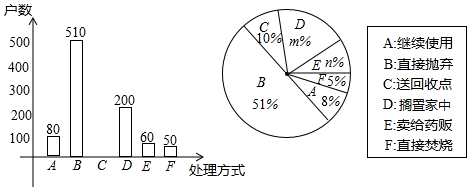
①m= ▲ , n= ▲ ;
②补全条形统计图;
③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
22. 如图,EF∥AD,∠1=∠2,求∠AGD的度数.请将解题过程填写完整.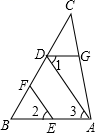
解:∵EF∥AD(已知),
∴∠2= ▲ ( ),
又∵∠1=∠2(已知),
∴∠1=∠3( ),
∴AB∥ ▲ ( ),
∴∠BAC+ ▲ =180°( ),
∵∠BAC=70°(已知),
∴∠AGD= ▲ .
23. 列方程组解应用题:小刚去文具店买1支钢笔,2个文具盒需要花70元,买2支钢笔,1个文具盒需要花50元,问:钢笔和文具盒的单价各多少元.24. 如图,若AE是△ABC边上的高,∠EAC的角平分线AD交BC于D,∠ACB=40°,求∠ADE.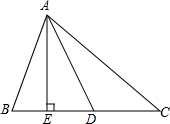 25. 为了迎接五一小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价180元;乙种服装每件进价150元,售价280元.(1)、若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?(2)、该专卖店为使甲、乙两种服装共200件的总利润(利润=售价-进价)不少于26700元,且不超过26800元,则该专卖店有几种进货方案?26. 在平面直角坐标系中,已知点A(a,0),B(b,3),C(4,0),且满足|a+b|+(a-b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.
25. 为了迎接五一小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价180元;乙种服装每件进价150元,售价280元.(1)、若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?(2)、该专卖店为使甲、乙两种服装共200件的总利润(利润=售价-进价)不少于26700元,且不超过26800元,则该专卖店有几种进货方案?26. 在平面直角坐标系中,已知点A(a,0),B(b,3),C(4,0),且满足|a+b|+(a-b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.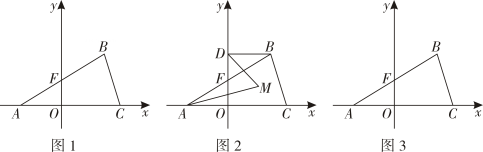 (1)、求出点A,B的坐标;(2)、如图2,若DB∥AC,∠BAC=a,且AM、DM分别平分∠CAB,∠ODB,求∠AMD(用含a的代数式表示).(3)、如图3,坐标轴上是否存在一点P,使得△ABP的面积和△ABC的面积相等?若存在请求出P点的坐标;若不存在,请说明理由.
(1)、求出点A,B的坐标;(2)、如图2,若DB∥AC,∠BAC=a,且AM、DM分别平分∠CAB,∠ODB,求∠AMD(用含a的代数式表示).(3)、如图3,坐标轴上是否存在一点P,使得△ABP的面积和△ABC的面积相等?若存在请求出P点的坐标;若不存在,请说明理由.