辽宁省盘锦市大洼重点中学2023-2024学年九年级上册数学期初试卷
试卷更新日期:2023-09-21 类型:开学考试
一、选择题(本大题共10小题,共20.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 若二次根式 有意义,则x的取值范围是( ).A、x> B、x≥ C、x≤ D、x≤52. 下列各式中是最简二次根式的是( )A、 B、 C、 D、3. 一元二次方程配方后可变形为 ( )A、 B、 C、 D、4. 一元二次方程的根的情况是 ( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根为 D、没有实数根5. 如图,在矩形ABCD中,对角线AC,BD交于点O,若∠COD=50°,那么∠CAD的度数是( )
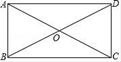 A、20° B、25° C、30° D、40°6. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、
A、20° B、25° C、30° D、40°6. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、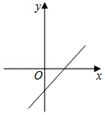 B、
B、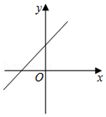 C、
C、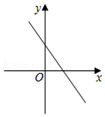 D、
D、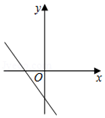 7. 某景点去年第一季度接待游客万人次,第二、第三季度共接待游客万人次.设该景点去年第一季度到第三季度的接待游客人次的增长率为且保持不变 , 则 ( )A、 B、 C、 D、8. 在中,、、分别为、、的对边,则下列条件中: , , ; , , ;;其中能判断是直角三角形的有 ( )A、个 B、个 C、个 D、个9. 如图,菱形中, , , 点是的中点,点由点出发,沿做匀速运动,到达点停止,则的面积与点经过的路程之间的函数关系的图象大致是 ( )
7. 某景点去年第一季度接待游客万人次,第二、第三季度共接待游客万人次.设该景点去年第一季度到第三季度的接待游客人次的增长率为且保持不变 , 则 ( )A、 B、 C、 D、8. 在中,、、分别为、、的对边,则下列条件中: , , ; , , ;;其中能判断是直角三角形的有 ( )A、个 B、个 C、个 D、个9. 如图,菱形中, , , 点是的中点,点由点出发,沿做匀速运动,到达点停止,则的面积与点经过的路程之间的函数关系的图象大致是 ( )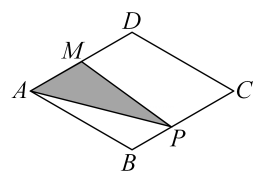 A、
A、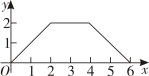 B、
B、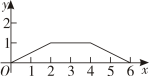 C、
C、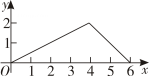 D、
D、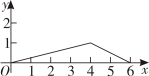 10. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(单位:km)与甲车行驶时间x(单位:h)之间的函数关系如图所示,根据图象提供的信息,下列结论错误的是( )
10. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(单位:km)与甲车行驶时间x(单位:h)之间的函数关系如图所示,根据图象提供的信息,下列结论错误的是( ) A、两城相距480千米 B、乙车比甲车晚出发1小时,却早到1小时 C、当乙车到达B城时,甲车距离B城80千米 D、甲车出发后4小时,乙车追上甲车
A、两城相距480千米 B、乙车比甲车晚出发1小时,却早到1小时 C、当乙车到达B城时,甲车距离B城80千米 D、甲车出发后4小时,乙车追上甲车二、填空题(本大题共6小题,共18.0分)
-
11. 将直线y=2x+1向下平移3个单位长度后所得直线的解析式是 .
12. 小红参加学校举办的“我爱我的祖国”主题演讲比赛,她的演讲内容、演讲能力、演讲效果得分分别为86分,72分,81分,若依次按照40%,30%,30%的百分比确定成绩,则她的平均成绩是分.13. 如图,在和中, , 是的中点,连接、若 , 则的长为 .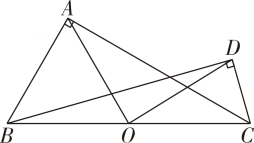 14. 一直角三角形的两边长分别为5和12,则第三边的长是 .15. 如图,在中,点是的中点,点是外一点, , 且平分 , 连接 , , 则的长为 .
14. 一直角三角形的两边长分别为5和12,则第三边的长是 .15. 如图,在中,点是的中点,点是外一点, , 且平分 , 连接 , , 则的长为 .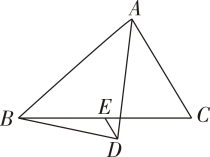 16. 如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则△BEF的面积为 .
16. 如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则△BEF的面积为 .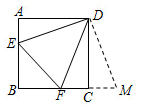
三、解答题(本大题共9小题,共82.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算:(1)、;(2)、 .18. 解方程:(1)、;(2)、 .19. 为了解中学生“平均每天体育锻炼时间”的情况,某地区教育部门随机调查了若干名中学生,根据调查结果制作统计图①和图②,请根据相关信息,解答下列问题:
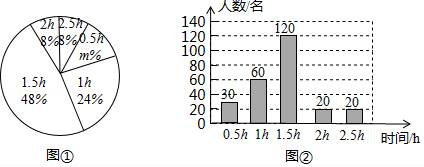 (1)、本次接受随机抽样调查的中学生人数为 , 图①中m的值是;(2)、求本次调查获取的样本数据的平均数、众数和中位数;(3)、根据统计数据,估计该地区250000名中学生中,每天在校体育锻炼时间大于等于1.5h的人数.20. 如图所示,在▱中,对角线与相交于点 , 过点任作一条直线分别交 , 于点 , .
(1)、本次接受随机抽样调查的中学生人数为 , 图①中m的值是;(2)、求本次调查获取的样本数据的平均数、众数和中位数;(3)、根据统计数据,估计该地区250000名中学生中,每天在校体育锻炼时间大于等于1.5h的人数.20. 如图所示,在▱中,对角线与相交于点 , 过点任作一条直线分别交 , 于点 , .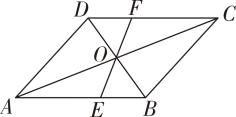 (1)、求证:;(2)、连接 , 直接写出当与满足什么关系时,四边形是菱形?21. 如图,已知过点B(1,0)的直线l1:y=kx+b与直线l2:y=2x+4相交于点P(a,2).
(1)、求证:;(2)、连接 , 直接写出当与满足什么关系时,四边形是菱形?21. 如图,已知过点B(1,0)的直线l1:y=kx+b与直线l2:y=2x+4相交于点P(a,2).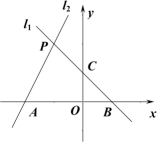 (1)、求直线l1的解析式;(2)、根据图象直接写出不等式的解集;(3)、求四边形PAOC的面积.22. 如图,长方形纸片中, , 将纸片折叠,使顶点落在边上的点处,折痕的一端点在边上
(1)、求直线l1的解析式;(2)、根据图象直接写出不等式的解集;(3)、求四边形PAOC的面积.22. 如图,长方形纸片中, , 将纸片折叠,使顶点落在边上的点处,折痕的一端点在边上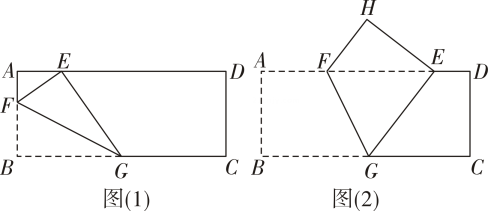 (1)、如图(1),当折痕的另一端在边上且时,求的长.(2)、如图(2),当折痕的另一端在边上且时,
(1)、如图(1),当折痕的另一端在边上且时,求的长.(2)、如图(2),当折痕的另一端在边上且时,①求证: .
②求的长.
23. 2022年,合肥蜀山区某商场于今年年初以每件元的进价购进一批商品.当商品售价为元时,三月份销售件.四、五月该商品十分畅销.销售量持续上涨.在售价不变的基础上,五月份的销售量达到件.(1)、求四、五这两个月的月平均增长率;(2)、从六月份起,商场为了减少库存,从而采用降价促销方式,经调查发现,该商品每降价元,月销量增加件,当商品降价多少元时,商场月获利元?24. 为提升学生的文学素养,培养学生的阅读兴趣,某校准备购进A,B两种图书.经调查,购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示,B种图书每本20元.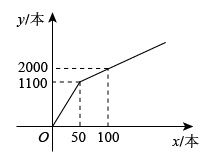 (1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.
(1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.①当时,求出w与x间的函数表达式;
②若购进A种图书不少于60本,且不超过B种图书本数的2倍,那么应该怎样分配购买A,B两种图书才能使总费用最少?最少总费用多少元?
25. 如图1,在中,为锐角,点为射线上一点,连接 , 以为一边且在的右侧作正方形 , 连接.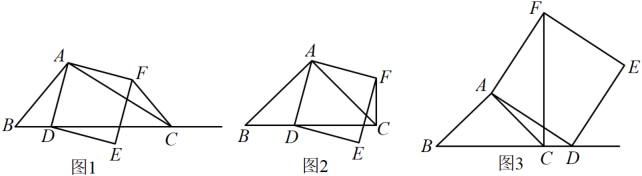 (1)、如果 ,
(1)、如果 ,①当点在线段上时(与点不重合),如图2,线段 , 所在直线的位置关系为 ▲ , 线段 , 的数量关系为 ▲ ;
②当点在线段的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)、如果 , 是锐角,点在线段上,当满足什么条件时,(点、不重合),请直接写出答案.