人教版2023-2024学年九年级上学期期中数学模拟试题（三）

试卷更新日期：2023-09-20 类型：期中考试

进入出卷网下载

一、选择题

1. 已知关于x的一元二次方程x²＋3x＋1＝0有两根为x₁和x₂ ，则x₁x₂＋x₁＋x₂的值是（）

A、2 B、－2 C、1 D、－1

查看试题解析
2. 抛物线 $y = 3 x_{}^{2} + 4$ 的顶点坐标是（）

A、（0，4） B、（0，－4） C、（－3，0） D、（3，0）

查看试题解析
3. 某果园2021年水果产量为100吨，2023年水果产量为144吨，求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为 $x$ ，则根据题意可列方程为（）

A、 $144 (1 - x)^{2} = 100$ B、 $100 (1 - x)^{2} = 144$ C、 $144 (1 + x)^{2} = 100$ D、 $100 (1 + x)^{2} = 144$

查看试题解析
4. 2020年-2022年无锡居民人均可支配收入由5.76万元增长至6.58万元，设人均可支配收入的平均增长率为x ，下列方程正确的是（）

A、5.76（1+x）²＝6.58 B、5.76（1+x²）＝6.58 C、5.76（1+2x）＝6.58 D、5.76x²＝6.58

查看试题解析
5. 下列图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 对于抛物线 $y = - 2 (x - 1)^{2} + 3$ ，下列判断正确的是（）

A、抛物线的开口向上 B、抛物线的顶点坐标是 $(- 1 ， 3)$ C、对称轴为直线 $x = 1$ D、当 $x = 3$ 时， $y > 0$

查看试题解析
7. 已知 $A (- 2 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (1 ， y_{3})$ 三点都在二次函数 $y = 2 (x + 1)^{2}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
8. 若关于 $x$ 的一元二次方程 $x^{2} + 6 x - a = 0$ 有实数根，则 $a$ 的取值范围是（）

A、 $a \leq - 9$ B、 $a > - 9$ C、 $a \geq - 9$ D、 $a \geq 9$

查看试题解析

二、填空题

9. 已知抛物线 $y = x^{2} + a - 3$ 的顶点在 $x$ 轴的下方，则 $a$ 的取值范围是.

查看试题解析
10. 如图，是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为"赵爽弦图"，它是由四个全等的直角三角形和一个小正方形组成的一个大正方形．设图中 AF = a ， DF = b ，连接 AE ， BE ，若△ ADE 与△ BEH 的面积相等，则 $\frac{a}{b} =$ .

查看试题解析
11. 若关于x的一元二次方程x²-2x+k＝0有两个不相等的实数根，则k的取值范围是．

查看试题解析
12. 在解一元二次方程x²+px+q＝0时，小红看错了常数项q ，得到方程的两个根是-3，1，小明看错了一次项系数p ，得到方程的两个根是5，-4，则原来的方程是．

查看试题解析
13. 已知二次函数 $y = a x^{2} + b x + c$ 的图象与x轴交于 $A (- 2 ， 0)$ 和 $B (m ， 0)$ ，其中 $2 < m < 4$ ，与y轴交于正半轴上一点．下列结论：① $a < 0$ ；② $4 c > \frac{b^{2}}{a}$ ；③若点 $C (- 1 ， y_{1})$ ， $D (2 ， y_{2})$ ， $E (4 ， y_{3})$ 均在二次函数图象上，则 $y_{3} < y_{1} < y_{2}$ ；④ $c + 8 a < 0$ ．其中一定正确的结论的序号是．

查看试题解析
14. 写出一个对称轴为y轴，且过 $(0 ， - 2)$ 的二次函数的解析式．

查看试题解析

三、解答题

15. 如果一元二次方程的两根相差 $1$ ，那么该方程称为“差 $1$ 方程” $.$ 例如 $x^{2} + x = 0$ 是“差 $1$ 方程”．

(1)、判断下列方程是不是“差 $1$ 方程”，”并说明由：
① $x^{2} - 5 x - 6 = 0$ ；
② $x^{2} - \sqrt{5} x + 1 = 0$ ；

(2)、已知关于 $x$ 的方程 $x^{2} - (m - 1) x - m = 0 (m$ 是常数 $)$ 是“差 $1$ 方程”，求 $m$ 的值；

(3)、若关于 $x$ 的方程 $a x^{2} + b x + 1 = 0 (a ， b$ 是常数， $a > 0)$ 是“差 $1$ 方程”，设 $t = 10 a - b^{2}$ ，求 $t$ 的最大值．

查看试题解析
16. 关于 $x$ 的方程 $(k - 1) x^{2} + 2 k x + 2 = 0$

(1)、求证：无论 $k$ 为何值，方程总有实数根．

(2)、设 $x_{1}$ ， $x_{2}$ 是方程 $(k - 1) x^{2} + 2 k x + 2 = 0$ 的两个根，记 $S = x_{1} x_{2} - x_{1} - x_{2}$ ， $S$ 的值能为1吗？若能，求出此时 $k$ 的值；若不能，请说明理由．

查看试题解析
17. 抛物线 $y_{1} = a x^{2} + b x - 3 (x \leq m)$ 的对称轴为直线 $x = 1$ ，与 $x$ 轴交于 $A (- 1 ， 0)$ 和 $B (m ， 0)$ ，与 $y$ 轴交于点 $C$ ，将 $y_{1}$ 沿直线 $x = m$ 作对称，得到抛物线 $y_{2}$ ．

(1)、求抛物线 $y_{2}$ 的解析式（写出自变量的取值范围）；

(2)、直线 $B C$ 与 $y_{2}$ 的另一个交点 $D$ ， $E$ ， $F$ 分别为线段 $B C$ ， $B D$ 上任意一点（不与 $B$ ， $C$ ， $D$ 重合），作 $E M ∥ y$ 轴， $F N ∥ y$ 轴，分别交 $y_{1}$ ， $y_{2}$ 于点 $M$ ， $N$ ，设 $E M$ 的最大值为 $d_{1}$ ， $F N$ 的最大值为 $d_{2}$ ，求证： $\frac{d_{1}}{d_{2}} = \frac{B C^{2}}{B D^{2}}$ ．

查看试题解析
18. 一运动员推铅球，铅球经过的路线为如图所示的抛物线.求铅球的落地点离运动员有多远（结果保留根号）？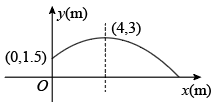

查看试题解析
19. 已知 $y_{1} = 2 x^{2}$ ，请写出一个二次函数 $y_{2}$ 同时满足以下两个条件：
①与 $y_{1}$ 函数图象开口大小、方向相同；
②当 $x > 1$ 时，y随x的增大而增大.

查看试题解析
20. 已知x₁ ， x₂是关于x的方程x²-2x+m-2=0的两个实数根，若3x₁+3x₂-x₁x₂=5，求m 的值.

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} + m x + n = 0$ 的两个实数根分别为 $x_{1} = - 2$ ， $x_{2} = 4$ ，求 $m + n$ 的值.

查看试题解析
22. 求函数 $y = - x^{2} + 4 x + 5$ 的最值，并说明是最大值还是最小值．

查看试题解析
23. 如图，已知一抛物线形大门，其地面宽度为10m，一身高为1.8m的同学站在门内，在离门脚1m处垂直地面站直拍照，其头顶恰好顶在抛物线形门上，根据这些条件，请你求出该大门的高h．

查看试题解析
24. 如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．若AE=1，求FM的长．

查看试题解析