人教版2023-2024学年九年级上学期期中数学模拟试题(二)
试卷更新日期:2023-09-20 类型:期中考试
一、选择题
-
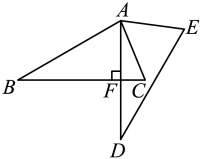
1. 如图,将绕点逆时针旋转得到 , 若且于点 , 则的度数为( )
 A、 B、 C、 D、2. 用公式法解方程时,求根公式中的 , , 的值分别是( )A、 , , B、 , , C、 , , D、 , ,3. 将抛物线y=2x2+2向左平移3个单位长度,再向上平移2个单位长度,得到抛物线的解析式是( )A、y=2(x+3)2+4 B、y=2(x+3)2 C、y=2(x-3)2+4 D、y=2(x-3)24. 若方程有实数根,则的取值范围是( )A、 B、且 C、 D、且5. 将绕点A逆时针旋转一定的角度后,得到 , 且点B的对应点D恰好落在边上,若 , 则的度数是 ( )
A、 B、 C、 D、2. 用公式法解方程时,求根公式中的 , , 的值分别是( )A、 , , B、 , , C、 , , D、 , ,3. 将抛物线y=2x2+2向左平移3个单位长度,再向上平移2个单位长度,得到抛物线的解析式是( )A、y=2(x+3)2+4 B、y=2(x+3)2 C、y=2(x-3)2+4 D、y=2(x-3)24. 若方程有实数根,则的取值范围是( )A、 B、且 C、 D、且5. 将绕点A逆时针旋转一定的角度后,得到 , 且点B的对应点D恰好落在边上,若 , 则的度数是 ( ) A、70° B、50° C、40° D、30°6. 已知点A(1,2)与点关于坐标原点对称,则实数a、b的值是( )A、a=1,b=2 B、a=-1,b=2 C、a=1,b=-2 D、a=-1,b=-27. 一元二次方程的二次项系数、一次项系数、常数项依次是( )A、1,-1,-3 B、1,-3,-1 C、2,-3,-1 D、2,-3,-28. 若 , 是方程的一个根,则值满足( )A、 B、 C、 D、
A、70° B、50° C、40° D、30°6. 已知点A(1,2)与点关于坐标原点对称,则实数a、b的值是( )A、a=1,b=2 B、a=-1,b=2 C、a=1,b=-2 D、a=-1,b=-27. 一元二次方程的二次项系数、一次项系数、常数项依次是( )A、1,-1,-3 B、1,-3,-1 C、2,-3,-1 D、2,-3,-28. 若 , 是方程的一个根,则值满足( )A、 B、 C、 D、二、填空题
-
9. 点关于原点O的对称点的坐标是.10. 已知、是方程的两根,则.11. 如图所示的抛物线是二次函数y=(m-2)x2-3x+m2+m-6的图象,那么m的值是.
 12. 线段在平面直角坐标系内,A点坐标为 , 线段绕原点O逆时针旋转 , 得到线段 , 则点的坐标为.13. 若关于x的一元二次方程有实数根,则k的取值范围是 .14. 一元二次方程的两个解分别为和 , 则.
12. 线段在平面直角坐标系内,A点坐标为 , 线段绕原点O逆时针旋转 , 得到线段 , 则点的坐标为.13. 若关于x的一元二次方程有实数根,则k的取值范围是 .14. 一元二次方程的两个解分别为和 , 则.三、解答题
-
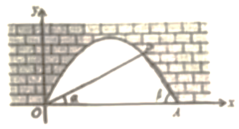
15. 把方程 先化成一元二次方程的一般形式,再写出它的二次项系数、一次项系数和常数项.16. 如图中是抛物线形拱桥,P处有一照明灯,水面宽 , 从O、A两处观测P处,仰角分别为、 . 且 , , 以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升 , 水面宽为多少?
 17. 将二次函数的解析式化为的形式,并指出该函数图象的开口方向、顶点坐标和对称轴.18. 如图,将△ABC绕点A逆时针旋转得到△ADE,点D在BC上,已知∠B=70°,求∠CDE的大小.
17. 将二次函数的解析式化为的形式,并指出该函数图象的开口方向、顶点坐标和对称轴.18. 如图,将△ABC绕点A逆时针旋转得到△ADE,点D在BC上,已知∠B=70°,求∠CDE的大小. 19. 已知关于x的一元二次方程 . 求证:方程总有两个实数根.20. 体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处点距离地面的高度为 , 当球运行的水平距离为时,达到最大高度的处(如图),问该学生把实心球扔出多远?(结果保留根号)
19. 已知关于x的一元二次方程 . 求证:方程总有两个实数根.20. 体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处点距离地面的高度为 , 当球运行的水平距离为时,达到最大高度的处(如图),问该学生把实心球扔出多远?(结果保留根号)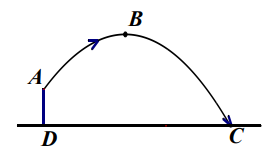 21. 在平面直角坐标系中,二次函数的对称轴为 , 且它经过点 , 求该二次函数的解析式和顶点坐标.
21. 在平面直角坐标系中,二次函数的对称轴为 , 且它经过点 , 求该二次函数的解析式和顶点坐标.
