人教版2023-2024学年九年级上学期期中数学模拟试题(一)
试卷更新日期:2023-09-20 类型:期中考试
一、选择题
-
1. 方程的解为( )A、 B、 C、 D、2. 下列中国传统吉祥图案中,不是中心对称图形的是( )A、
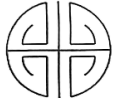 B、
B、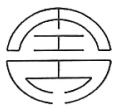 C、
C、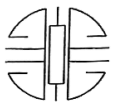 D、
D、 3. 用配方法解方程 , 配方正确的是( )A、 B、 C、 D、4. 如图,在Rt△ABC中, , , , 将△ABC绕点C按逆时针方向旋转得到 , 此时点恰好在边AB上,则点与点B之间的距离为( )
3. 用配方法解方程 , 配方正确的是( )A、 B、 C、 D、4. 如图,在Rt△ABC中, , , , 将△ABC绕点C按逆时针方向旋转得到 , 此时点恰好在边AB上,则点与点B之间的距离为( ) A、4 B、2 C、3 D、5. 已知关于x的一元二次方程(其中p,q为常数)有两个相等的实数根,则下列结论中,错误的是( ).A、1可能是方程的根 B、可能是方程的根 C、0可能是方程的根 D、1和都是方程的根6. 如图1,校运动会上,初一的同学们进行了投实心球比赛.我们发现,实心球在空中飞行的轨迹可以近似看作是抛物线.如图2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是y= , 则该同学此次投掷实心球的成绩是( )
A、4 B、2 C、3 D、5. 已知关于x的一元二次方程(其中p,q为常数)有两个相等的实数根,则下列结论中,错误的是( ).A、1可能是方程的根 B、可能是方程的根 C、0可能是方程的根 D、1和都是方程的根6. 如图1,校运动会上,初一的同学们进行了投实心球比赛.我们发现,实心球在空中飞行的轨迹可以近似看作是抛物线.如图2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是y= , 则该同学此次投掷实心球的成绩是( ) A、2m B、6m C、8m D、10m7. 等腰三角形的两边的长是方程两个根,则此三角形的周长是( )A、7 B、8 C、7或8 D、以上都不对8. 一个等腰三角形的两条边长分别是方程x2-9x+18=0的两根,则该等腰三角形的周长是( )A、12 B、9 C、15 D、12或15
A、2m B、6m C、8m D、10m7. 等腰三角形的两边的长是方程两个根,则此三角形的周长是( )A、7 B、8 C、7或8 D、以上都不对8. 一个等腰三角形的两条边长分别是方程x2-9x+18=0的两根,则该等腰三角形的周长是( )A、12 B、9 C、15 D、12或15二、填空题
-
9. 将二次函数 y=x2+2的图象向上平移 3 个单位长度,得到的图象所对应的函数解析式是 .10. 关于抛物线 +4,给出下列说法:
①抛物线开口向下,顶点是(0,4).
②当 时,随的增大而减小.
③当时, .
④若 (m,p)(n,p)是该抛物线上两个不同的点,则 .
其中正确的说法有.(填序号)
11. 已知x1 , x2是方程2x2-3x+1=0的两根,则代数式的值为 .12. 若是方程的一个根,则的值为 .13. 如图,将△ABC绕着点顺时针旋转到△ADE的位置,使点首次落在上.已知 , , 则 . 14. 若关于的一元二次方程有实数根,则常数的范围是 .
14. 若关于的一元二次方程有实数根,则常数的范围是 .三、解答题
-
15. 已知二次函数+8的图像如图所示,与坐标轴的交点分别为A、B、C.
 (1)、求此函数解析式,及A、B、C的坐标,(2)、如果点 是此二次函数的图象上一点,若 , 则 的取值范围为(直接写出结果)(3)、在x轴上方的抛物线上是否存在点D,使得△ABD的面积为8,若存在,请求出点D的坐标;若不存在,请说明理由.16. 已知是方程的一个根,求的值及方程的另一根 .17. 已知关于的一元二次方程 .(1)、若是该方程的一个根,求的值;(2)、若一元二次方程有实数根,求的取值范围.18. 已知点为二次函数图像上的点,求代数式的值.19. 在平面直角坐标系中,与轴交于点 .
(1)、求此函数解析式,及A、B、C的坐标,(2)、如果点 是此二次函数的图象上一点,若 , 则 的取值范围为(直接写出结果)(3)、在x轴上方的抛物线上是否存在点D,使得△ABD的面积为8,若存在,请求出点D的坐标;若不存在,请说明理由.16. 已知是方程的一个根,求的值及方程的另一根 .17. 已知关于的一元二次方程 .(1)、若是该方程的一个根,求的值;(2)、若一元二次方程有实数根,求的取值范围.18. 已知点为二次函数图像上的点,求代数式的值.19. 在平面直角坐标系中,与轴交于点 . (1)、求点的坐标以及抛物线的对称轴;(2)、抛物线与直线交于点 , , 其中
(1)、求点的坐标以及抛物线的对称轴;(2)、抛物线与直线交于点 , , 其中①当时,求抛物线的表达式;
②当时,请直接写出的取值范围.
20. 已知:关于x的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程的一根是另一根的2倍,求k的值.21. 如图,在中, , 将绕点A顺时针方向旋转到的位置,连接 , 求的度数.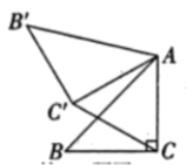 22. 新冠病毒肆虐全球,我国的疫情很快得到了控制,并且研发出安全性、有效性均非常高的疫苗.经调查发现,北京生物制药厂有1条生产线,最大产能是42万支/天,若每增加1条生产线,每条生产线的最大产能将减少2万支/天,现该厂要保证每天生产疫苗144万支,在既增加产能的同时又节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
22. 新冠病毒肆虐全球,我国的疫情很快得到了控制,并且研发出安全性、有效性均非常高的疫苗.经调查发现,北京生物制药厂有1条生产线,最大产能是42万支/天,若每增加1条生产线,每条生产线的最大产能将减少2万支/天,现该厂要保证每天生产疫苗144万支,在既增加产能的同时又节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
