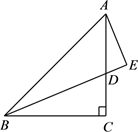人教版2023-2024学年八年级上学期期中数学模拟试题(三)
试卷更新日期:2023-09-20 类型:期中考试
一、选择题
-
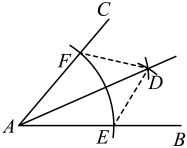
1. 如图,以顶点A为圆心,适当长为半径画弧,分别交 , 于点E、F,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点D,作射线 , 则说明的依据是( )
 A、 B、 C、 D、2. 十二边形的外角和的度数为( )A、 B、 C、 D、3. 如图, , 交于点C,于D,若 , 则等于( )
A、 B、 C、 D、2. 十二边形的外角和的度数为( )A、 B、 C、 D、3. 如图, , 交于点C,于D,若 , 则等于( ) A、3 B、2 C、1.5 D、14. 已知三角形的两边长分别为5和9,则该三角形的第三边长可能是( )A、3 B、4 C、5 D、145. 如图,点O是△ABC内一点,∠ABO=30°,∠ACO=15°,∠BOC=100°,则∠A的度数为( )
A、3 B、2 C、1.5 D、14. 已知三角形的两边长分别为5和9,则该三角形的第三边长可能是( )A、3 B、4 C、5 D、145. 如图,点O是△ABC内一点,∠ABO=30°,∠ACO=15°,∠BOC=100°,则∠A的度数为( ) A、40° B、45° C、55° D、不能确定6. 如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带( )去最省事.
A、40° B、45° C、55° D、不能确定6. 如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带( )去最省事.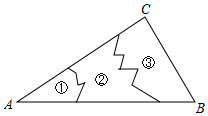 A、① B、② C、③ D、①③7. 下列图标中,是轴对称图的是( )A、
A、① B、② C、③ D、①③7. 下列图标中,是轴对称图的是( )A、 B、
B、 C、
C、 D、
D、 8. 若点P(a,-1)关于y轴的对称点为Q(-2,b),则a+b的值是( )A、-1 B、0 C、1 D、2
8. 若点P(a,-1)关于y轴的对称点为Q(-2,b),则a+b的值是( )A、-1 B、0 C、1 D、2二、填空题
-
9. 八边形的内角和是外角和的倍.10. 如图,在等腰三角形中, , 垂直平分 , 交于点 , 交于点.若 , 则.
 11. 点和点关于轴对称,则.12. 如图,在中,和的平分线交于点 , 过点作交于点 , 交于点 , 若 , , , 则的周长为.
11. 点和点关于轴对称,则.12. 如图,在中,和的平分线交于点 , 过点作交于点 , 交于点 , 若 , , , 则的周长为. 13. 如图,平分 , 于点 , 点为射线上一动点,若 , 则的最小值为 .
13. 如图,平分 , 于点 , 点为射线上一动点,若 , 则的最小值为 . 14. 如图,若 , , , , 则的周长为 .
14. 如图,若 , , , , 则的周长为 .
三、解答题
-
15. 如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.
求证:AD平分∠BAC.
 16. 如图,在△ABC中,AB=AC, , 点D、E在BC上,AD⊥AC,AE⊥AB.求证:为等边三角形.
16. 如图,在△ABC中,AB=AC, , 点D、E在BC上,AD⊥AC,AE⊥AB.求证:为等边三角形. 17. 如图,、分别在、上,是的中点, , 求证: .
17. 如图,、分别在、上,是的中点, , 求证: . 18. 如图, , , , .求的度数.
18. 如图, , , , .求的度数. 19. 已知:如图,在中, , 点D、E分别在边AC、AB上,且 , BD与CE相交于点O.求证:.
19. 已知:如图,在中, , 点D、E分别在边AC、AB上,且 , BD与CE相交于点O.求证:. 20. 如图,在中,与的平分线相交于点O,AO的延长线交于点D,.求证:.
20. 如图,在中,与的平分线相交于点O,AO的延长线交于点D,.求证:. 21. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数.
21. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数.