人教版2023-2024学年八年级上学期期中数学模拟试题(二)
试卷更新日期:2023-09-20 类型:期中考试
一、选择题
-
1. 如图,的顶点在的边上,且 , , , 则下列说法不正确的是( )
 A、≌ B、 C、 D、2. 数学活动课上,小明想用三根木棒首尾顺次相接制作一个三角形模型,现有两根长度分别为和的木棒,则第三根木棒的长度可取( )A、 B、 C、 D、3. 如图,AB和CD相交于点O,则下列结论不正确的是( )
A、≌ B、 C、 D、2. 数学活动课上,小明想用三根木棒首尾顺次相接制作一个三角形模型,现有两根长度分别为和的木棒,则第三根木棒的长度可取( )A、 B、 C、 D、3. 如图,AB和CD相交于点O,则下列结论不正确的是( ) A、∠1=∠2 B、∠1=∠A+∠C C、∠2>∠D D、∠A+∠D=∠B+∠C4. 如图,中,的垂直平分线交AB于点 , 交BC于点E,AC的垂直平分线交AC于点F,交BC于点.若以BE,EG,GC为边的三角形的面积为8,则的面积可能是( )
A、∠1=∠2 B、∠1=∠A+∠C C、∠2>∠D D、∠A+∠D=∠B+∠C4. 如图,中,的垂直平分线交AB于点 , 交BC于点E,AC的垂直平分线交AC于点F,交BC于点.若以BE,EG,GC为边的三角形的面积为8,则的面积可能是( ) A、12 B、14 C、16 D、185. △ABC中,AB=AC,CD为AB上的高,且△ADC为等腰三角形,则∠BCD等于( )A、或 B、或 C、或 D、或6. 如图,直线CD是线段AB的垂直平分线,Р为直线CD上的一点.已知△PAB的周长为14,PA=4,则线段AB的长度为( )
A、12 B、14 C、16 D、185. △ABC中,AB=AC,CD为AB上的高,且△ADC为等腰三角形,则∠BCD等于( )A、或 B、或 C、或 D、或6. 如图,直线CD是线段AB的垂直平分线,Р为直线CD上的一点.已知△PAB的周长为14,PA=4,则线段AB的长度为( ) A、6 B、5 C、4 D、37. 如图,已知 , , , 则 , , 三者之间的关系是( )
A、6 B、5 C、4 D、37. 如图,已知 , , , 则 , , 三者之间的关系是( )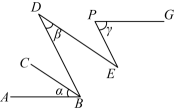 A、 B、 C、 D、8. 在平面直角坐标系中,点A的坐标为 , 点B与点A关于x轴对称,则点B的坐标为( )A、 B、 C、 D、
A、 B、 C、 D、8. 在平面直角坐标系中,点A的坐标为 , 点B与点A关于x轴对称,则点B的坐标为( )A、 B、 C、 D、二、填空题
-
9. 如图,平分 , , , 垂足分别为 , , , , 则 .
 10. 如图,BD垂直平分垂直平分AF于 , 若 , 则的周长为.
10. 如图,BD垂直平分垂直平分AF于 , 若 , 则的周长为. 11. 如图,中的垂直平分线交AB于 , 交边AC于点的周长等于 , 则的周长等于.
11. 如图,中的垂直平分线交AB于 , 交边AC于点的周长等于 , 则的周长等于. 12. 如图,在中,为中点,为边上的动点,连接 , 交的延长线于点 , 若 , 则的值是.
12. 如图,在中,为中点,为边上的动点,连接 , 交的延长线于点 , 若 , 则的值是. 13. 三角形三边长为7、12、a,则a的取值范围是 .14. 如图,为线段上一动点不与点、重合 , 在同侧分别作正和正 , 与交于点 , 与交于点 , 与交于点 , 连接以下五个结论:;;;; .
13. 三角形三边长为7、12、a,则a的取值范围是 .14. 如图,为线段上一动点不与点、重合 , 在同侧分别作正和正 , 与交于点 , 与交于点 , 与交于点 , 连接以下五个结论:;;;; .恒成立的结论有把你认为正确的序号都填上

三、解答题
-
15. 如图,在中, , 是边上的中线,的垂直平分线分别交、、于点、、 , 连接 , .
 (1)、试说明:;(2)、若 , 求的度数.16. 如图,在四边形中, , 点 , 分别是 , 的中点, , .试说明:.
(1)、试说明:;(2)、若 , 求的度数.16. 如图,在四边形中, , 点 , 分别是 , 的中点, , .试说明:. 17. 要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,为卡钳两柄交点(即交于点),且有.如果圆形工件恰好通过卡钳 , 则此工件的外径必是的长.你能说明其中的道理吗?
17. 要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,为卡钳两柄交点(即交于点),且有.如果圆形工件恰好通过卡钳 , 则此工件的外径必是的长.你能说明其中的道理吗? 18. 如图,已知中, , 点D、E在直线BC上, .
18. 如图,已知中, , 点D、E在直线BC上, . (1)、如图1,求证:;(2)、如图2,过点D向下作 , 交AB的延长线于点F,若 , , 求证:;(3)、如图3,在(2)的条件下,延长FD、EA交于点G,连接BG,若 , 求四边形ACBG的面积.19. 某蔬菜店第一次用元购进某种蔬菜,由于销售状况良好,该店又用元第二次购进该品种蔬菜,所购数量是第一次购进数量的倍,但进货价每千克少了元.(1)、第一次所购该蔬菜的进货价是每千克多少元?(2)、蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有的损耗,第二次购进的蔬菜有的损耗,若该蔬菜店售完这些蔬菜获利不低于元,则该蔬菜每千克售价是多少元?20. 如图,点 , , 在一条直线上,、均为等边三角形,连接和 , 分别交 , 于点 , , 交于点 .
(1)、如图1,求证:;(2)、如图2,过点D向下作 , 交AB的延长线于点F,若 , , 求证:;(3)、如图3,在(2)的条件下,延长FD、EA交于点G,连接BG,若 , 求四边形ACBG的面积.19. 某蔬菜店第一次用元购进某种蔬菜,由于销售状况良好,该店又用元第二次购进该品种蔬菜,所购数量是第一次购进数量的倍,但进货价每千克少了元.(1)、第一次所购该蔬菜的进货价是每千克多少元?(2)、蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有的损耗,第二次购进的蔬菜有的损耗,若该蔬菜店售完这些蔬菜获利不低于元,则该蔬菜每千克售价是多少元?20. 如图,点 , , 在一条直线上,、均为等边三角形,连接和 , 分别交 , 于点 , , 交于点 .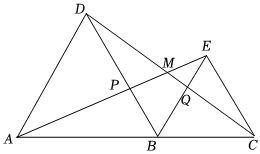 (1)、求证:≌;(2)、求的度数.21. 已知:如图,点B,F,C,E在一条直线上, , , 且.求证:.
(1)、求证:≌;(2)、求的度数.21. 已知:如图,点B,F,C,E在一条直线上, , , 且.求证:. 22. 如图,点为的边的延长线上一点,过点作于点 , 交于点 , 若 , , 求的度数.
22. 如图,点为的边的延长线上一点,过点作于点 , 交于点 , 若 , , 求的度数. 23. 已知,在中, , , , 三点都在直线上, .
23. 已知,在中, , , , 三点都在直线上, .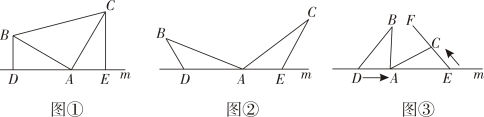 (1)、如图 , 若 , 则与的数量关系为 , , 与的数量关系为 .(2)、如图 , 当不垂直于时,中的结论是否成立?请说明理由.(3)、如图 , 若只保持 , , , 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为是否存在 , 使得与全等?若存在,求出相应的与的值;若不存在,请说明理由.24. 如图 , 已知直线 , 且和 , 分别交于 , 两点,和 , 分别交于 , 两点,点在线段上, , , .
(1)、如图 , 若 , 则与的数量关系为 , , 与的数量关系为 .(2)、如图 , 当不垂直于时,中的结论是否成立?请说明理由.(3)、如图 , 若只保持 , , , 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为是否存在 , 使得与全等?若存在,求出相应的与的值;若不存在,请说明理由.24. 如图 , 已知直线 , 且和 , 分别交于 , 两点,和 , 分别交于 , 两点,点在线段上, , , . (1)、若 , , 则 .(2)、试找出 , , 之间的数量关系,并说明理由.(3)、应用(2)中的结论解答下面的问题:
(1)、若 , , 则 .(2)、试找出 , , 之间的数量关系,并说明理由.(3)、应用(2)中的结论解答下面的问题:如图 , 点在的北偏东的方向上,在的北偏西的方向上,求的度数.
(4)、如果点在直线上且在线段外侧运动点和 , 两点不重合 , 其他条件不变,试探究 , , 之间的关系.