人教版2023-2024学年八年级上学期期中数学模拟试题(一)
试卷更新日期:2023-09-20 类型:期中考试
一、选择题
-
1. 已知等腰△ABC的两边长分别为2和3,则等腰△ABC的周长为( )A、7 B、8 C、6或8 D、7或82. 如图所示.在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=6cm,∠B=15°,则AC等于( )
 A、6cm B、5cm C、4cm D、3cm3. 如图, , 平分 , D是的中点, , 则( )
A、6cm B、5cm C、4cm D、3cm3. 如图, , 平分 , D是的中点, , 则( )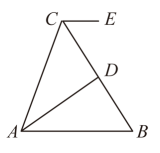 A、 B、 C、 D、4. 如图,中, , 点在上, , 若 , 则的度数是( )
A、 B、 C、 D、4. 如图,中, , 点在上, , 若 , 则的度数是( ) A、 B、 C、 D、5. 下面各图中所给数据的三角形,则甲、乙、丙三个三角形和左侧全等的是( )
A、 B、 C、 D、5. 下面各图中所给数据的三角形,则甲、乙、丙三个三角形和左侧全等的是( )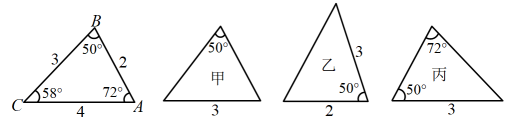 A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙6. 下列图案中,是轴对称图形的是( )A、
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙6. 下列图案中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,在中, , , 平分 , , 是边上一动点,则 , 之间的最小距离为( )
7. 如图,在中, , , 平分 , , 是边上一动点,则 , 之间的最小距离为( ) A、2 B、3 C、4 D、68. 如图,过边长为的等边三角形的边上一点 , 作于点为延长线上一点,当时,交于 , 则的长为( )
A、2 B、3 C、4 D、68. 如图,过边长为的等边三角形的边上一点 , 作于点为延长线上一点,当时,交于 , 则的长为( ) A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
9. 等腰中, , 顶角A为 , 平面内有一点P,满足且 , 则的度数为 .10. 如图,点B、F、C、E在一条直线上, , , 若用“”判定 , 则添加的一个条件是 .
 11. 若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为 .12. 如图,C为线段AB上一动点(不与点A、B重合),在AB的上方分别作△ACD和△BCE,且AC=DC,BC=EC,∠ACD=∠BCE,AE、BD交于点P.有下列结论:①②;③当时,; ④PC平分∠APB.其中正确的是.(把你认为正确结论的序号都填上)
11. 若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为 .12. 如图,C为线段AB上一动点(不与点A、B重合),在AB的上方分别作△ACD和△BCE,且AC=DC,BC=EC,∠ACD=∠BCE,AE、BD交于点P.有下列结论:①②;③当时,; ④PC平分∠APB.其中正确的是.(把你认为正确结论的序号都填上)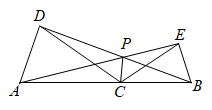 13. 已知:在中, , 垂足为点 , 若 , , 则.14. 如图,∠AOB=30°,点P位于∠AOB内,OP=3,点M,N分别是射线OA、OB边上的动点,当△PMN的周长最小时,最小周长为.
13. 已知:在中, , 垂足为点 , 若 , , 则.14. 如图,∠AOB=30°,点P位于∠AOB内,OP=3,点M,N分别是射线OA、OB边上的动点,当△PMN的周长最小时,最小周长为.
三、解答题
-
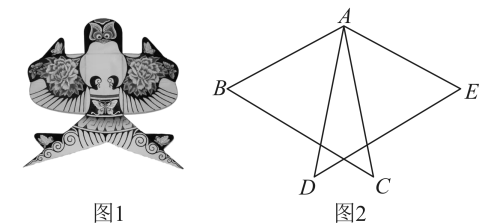
15. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , , 求 .
 16. 如图, , , , 平分 , 若 , 求的长.
16. 如图, , , , 平分 , 若 , 求的长. 17. 如图所示,已知CD=BD,点E、F分别是CD、BD的中点,∠CAF=∠BAE,∠B=∠C.求证:AE=AF.
17. 如图所示,已知CD=BD,点E、F分别是CD、BD的中点,∠CAF=∠BAE,∠B=∠C.求证:AE=AF. 18. 如图,在中,的垂直平分线交于点E,交于点F,点D为的中点,连接 , 此时 , . 求证: .
18. 如图,在中,的垂直平分线交于点E,交于点F,点D为的中点,连接 , 此时 , . 求证: . 19. 骑自行车旅行越来越受到人们的喜爱,顺风车行经营的型车2017年7月份销售额为3.2万元,今年经过改造升级后,型车每辆的销售价比去年增加400元,若今年7月份与去年7月份卖出的型车数量相同,则今年7月份型车销售总额将比去年7月份销售总额增加25%.求今年7月份顺风车行型车每辆的销售价格.20. 如图,工人师傅要检查三角形工件ABC的和是否相等,但他手边没有量角器,只有一个刻度尺,他是这样操作的:
19. 骑自行车旅行越来越受到人们的喜爱,顺风车行经营的型车2017年7月份销售额为3.2万元,今年经过改造升级后,型车每辆的销售价比去年增加400元,若今年7月份与去年7月份卖出的型车数量相同,则今年7月份型车销售总额将比去年7月份销售总额增加25%.求今年7月份顺风车行型车每辆的销售价格.20. 如图,工人师傅要检查三角形工件ABC的和是否相等,但他手边没有量角器,只有一个刻度尺,他是这样操作的:
①分别在BA和CA上取
②在BC上取
③连接DE、FG,量出DE的长为a米,FG的长为b米.
若 , 则说明和是相等的,他的这种做法合理吗?为什么?
21. 已知:如图,点D在线段AC上,点B在线段AE上,AE=AC,BE=DC,求证:∠E=∠C.


