人教版2023-2024学年七年级上学期期中数学模拟试题（四）

试卷更新日期：2023-09-20 类型：期中考试

进入出卷网下载

一、选择题

1. 已知两个有理数 $a$ ， $b$ ，如果 $a b < 0$ 且 $a + b > 0$ ，那么（）

A、 $a > 0$ ， $b > 0$ B、 $a < 0$ ， $b > 0$ C、 $a$ 、 $b$ 异号，且正数的绝对值较大 D、 $a$ 、 $b$ 异号，且负数的绝对值较大

查看试题解析
2. 下列各组数中，数值相等的是（）

A、 $(- 3)^{2}$ 和 $(- 2)^{3}$ B、 $(- 3)^{4}$ 和 $- 3^{4}$ C、 $- 1^{3}$ 和 $(- 1)^{3}$ D、 $- (3 \times 2)^{2}$ 和 $- 3 \times 2^{2}$

查看试题解析
3. 小明在写作业时不慎将两滴墨水滴在数轴上，如图所示，此时墨迹盖住的整数共有（）个．

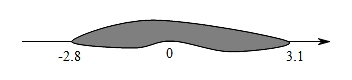A、3 B、4 C、5 D、6

查看试题解析
4. 2022年春季开学后，济南市的天气突然降温，2月16日的最高气温是 $2 ℃$ ，最低气温是 $- 4 ℃$ ，那么这天的温差是（）

A、 $6 ℃$ B、 $- 6 ℃$ C、 $2 ℃$ D、 $- 2 ℃$

查看试题解析
5. 有理数a，b在数轴上对应的位置如图所示，则（）

A、 $| a | < | b |$ B、 $a b > 0$ C、 $a + b < 0$ D、 $a - b > 0$

查看试题解析
6. 若 $| x | = 7 ， | y | = 9$ ，则 $x - y$ 为（）

A、 $\pm 2$ 和 $\pm 16$ B、 $\pm 16$ C、 $- 2$ 和 $- 16$ D、 $\pm 2$

查看试题解析
7. 如图，在一个不完整的数轴上有 $A$ ， $B$ ， $C$ 三个点，若点 $A$ ， $B$ 表示的数互为相反数，则图中点 $C$ 点表示的数是（）

A、 $- 2$ B、 $1$ C、 $0$ D、 $4$

查看试题解析
8. 数轴上-2.1和3.9之间的整数有（）

A、4个 B、5个 C、6个 D、7个

查看试题解析

二、填空题

9. 如果把汽车向东行驶 $80 k m$ 记作 $+ 80 k m$ ，那么汽车向西行驶 $100 k m$ 应记作km.

查看试题解析
10. 单项式 $- \frac{2 π a^{2} b^{5} c}{3}$ 的系数是，次数是.

查看试题解析
11. 如图是一个正方体的表面展开图，则原正方体中与“你”字相对应的的字是．

查看试题解析
12. 如图，图中的所有正方形都完全相同，在图中的①②③④某一位置放一个相同的正方形，所围成的图形不能围成正方体的位置是．（填序号）

查看试题解析
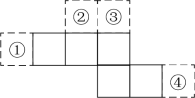13. 近似数68.4万精确到位．

查看试题解析
14. 如图，用三个同（1）图的长方形和两个同（2）图的长方形用两种方式去覆盖一个大的长方形 $A B C D$ ，两种方式未覆盖的部分（阴影部分）的周长一样，那么（1）图中长方形的面积 $S_{1}$ 与（2）图长方形的面积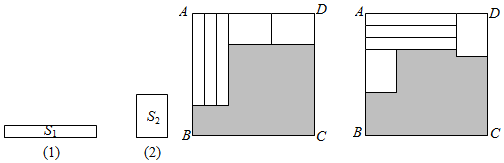 $S_{2}$ 的比是.

查看试题解析

三、解答题

15. 画一条数轴，然后在数轴上标出下列各数，并把这四个数用“ $>$ ”号连接起来.
$- 3 ， 0 ， - 1 \frac{1}{2} ， 3$

查看试题解析
16. 已知 $| x | = 5 ， | y | = 3$ ，若 $x - y > 0$ ，求 $x + y$ 的值．

查看试题解析
17. 如图：已知线段AB＝20cm，在AB上取一点P，M是AB的中点，N是AP中点，若MN＝3cm，求线段AP的长.

查看试题解析
18. 动物园在检测成年麦哲伦企鹅的身体状况时，最重要的一项工作就是称体重，已知某动物园对6只成年麦哲伦企鹅进行称重检测，以4千克为标准，超过或不足的千克数分别用正数和负数表示，称重记录如下表所示，求这6只企鹅的总体重

编号

1

2

3

4

5

6

差值（kg）

-0.08

+0.09

+0.05

-0.05

+0.08

+0.06

查看试题解析
19. 先化简，再求值：3x²y+[-3(x²y+1)+2xy+1]，其中x=-4，y= $\frac{1}{2}$

查看试题解析
20. 已知 $A = 2 x^{2} - x + 6$ ， $B = 3 x^{2} - 4 x - 1$ ，求 $2 A + B$ ．

查看试题解析
21. 若一xy^|a|与3x^|2b+1|y是同类项，其中a、b互为倒数，求2（a-2b²）- $\frac{1}{2}$ （3b²-a）的值。

查看试题解析
22. 如图，已知 $∠ A O C ： ∠ B O C = 1 ： 5$ ， $O D$ 平分 $∠ A O B$ ，且 $∠ C O D = 36 °$ ，求 $∠ A O B$ 的度数.

查看试题解析
23. 数轴是一个非常重要的数学工具，实数和数轴上的点能建立一一对应的关系，它建立了数与形的联系，是初中“数形结合”的基础。我们知道一个数在数轴上对应的点到原点的距离叫做这个数的绝对值，如： $| - 3 | = 3$ ， $| x |$ ：表示数 $x$ 的点到原点的距离。同样的， $| x - 3 |$ ：表示数 $x$ 的点到表示数3的点的距离。请结合数轴解决下列问题：

①当 $x = 5$ 时， $| x - 3 |$ 表示什么意思？；

②若 $| x - 3 | = 5$ ，则 $x =$ ；

③若 $| x - 2 | + | x + 3 | = 7$ ，则 $x$ 的值是；

④求使 $| x - 4 | + | x + 1 |$ 的值最小的所有符合条件的整数 $x$ .

查看试题解析
24. 如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走均为正，向下向左走均为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向．

(1)、图中A→C（，），B→C（，），C→（+1，﹣2）；

(2)、若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置；

(3)、若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．

(4)、若图中另有两个格点M、N，且M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），则N→A应记为什么？

查看试题解析

编号	1	2	3	4	5	6
差值（kg）	-0.08	+0.09	+0.05	-0.05	+0.08	+0.06