人教版2023-2024学年七年级上学期期中数学模拟试题(一)
试卷更新日期:2023-09-20 类型:期中考试
一、选择题
-
1. 下列各数中,绝对值最大的数是( )A、 B、 C、 D、2. 下列运用等式性质进行的变形中,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 某车间原计划用15小时生产一批零件,实际每小时多生产了10件,用了13小时不但完成了任务,而且还多生产了80件,设原计划每小时生产个零件,那么下列方程正确的是( )A、 B、 C、 D、4. 等于( )A、2 B、-2 C、 D、05. 已知有理数在数轴上的位置如图所示,下列结论正确的是( )
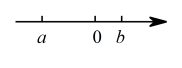 A、 B、 C、 D、6. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:
A、 B、 C、 D、6. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:
乙:
丙:
丁:
其中正确的是( )
 A、甲乙 B、丙丁 C、甲丙 D、乙丁7. 一个骰子相对两面的点数之和为 , 它的展开图如图,下列判断正确的是( )
A、甲乙 B、丙丁 C、甲丙 D、乙丁7. 一个骰子相对两面的点数之和为 , 它的展开图如图,下列判断正确的是( ) A、代表
A、代表 B、代表
B、代表 C、代表
C、代表  D、代表
D、代表 8. 首届全国青运会于2015年10月18日在福州举行,据统计,共有28600名志愿者,将负责赛会服务、城市宣传、交通指引等工作,将这个数字用科学记数法表示为( ).A、286× B、28.6× C、2.86× D、2.86×
8. 首届全国青运会于2015年10月18日在福州举行,据统计,共有28600名志愿者,将负责赛会服务、城市宣传、交通指引等工作,将这个数字用科学记数法表示为( ).A、286× B、28.6× C、2.86× D、2.86×二、填空题
-
9. 已知与互余,且 , 则的补角是度.10. 计算11. 《九章算术》中注有“今两算得失相反,要另正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.有一种记分法:85分以上,如88分记作+3分,某同学得分80分,则应记作 分.12. 数a,b在数轴上对应点的位置如图所示,化简a-|b-a|= .
 13. 如果单项式与的和是单项式,那么.14. 从、、、、几个数中任取三个数相乘,所得到的最大乘积是.
13. 如果单项式与的和是单项式,那么.14. 从、、、、几个数中任取三个数相乘,所得到的最大乘积是.三、解答题
-
15. 已知:a 与 b 互为相反数,c 与 d 互为倒数,当 时,求代数式的值.16. 一位同学在做题时,原题为某式减去 , 因粗心误认为加上此式而得到错误的答案 , 试求原题应得的正确答案.17. 阅读下面文字:
对于可以按如下方法进行计算:
原式
.
上面这种方法叫拆项法,你看懂了吗?仿照上面的方法,请你计算:
18. 如图,是一个几何体的表面展开图,依据图中数据求该几何体的表面积和体积.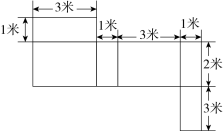 19. 如图,线段 , 线段 , 点M是的中点,在上取一点N,使得 , 求的长.
19. 如图,线段 , 线段 , 点M是的中点,在上取一点N,使得 , 求的长.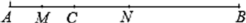 20. 有理数a、b、c的位置如图所示,化简.
20. 有理数a、b、c的位置如图所示,化简. 21. 已知a、b互为倒数,c、d互为相反数,m为最大的负整数,n的绝对值为2,试求的值.22. 如果关于x、y的多项式是三次三项式,试探讨m、n的取值情况.23. 如图所示,已知 , 从点出发的一条射线满足 , 是的平分线,是的平分线,请补全图形(画出正确的草图即可),并求出的大小.
21. 已知a、b互为倒数,c、d互为相反数,m为最大的负整数,n的绝对值为2,试求的值.22. 如果关于x、y的多项式是三次三项式,试探讨m、n的取值情况.23. 如图所示,已知 , 从点出发的一条射线满足 , 是的平分线,是的平分线,请补全图形(画出正确的草图即可),并求出的大小.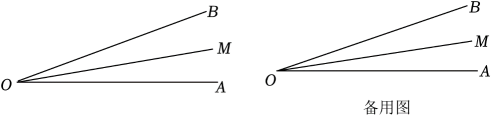 24. 某种茶叶,若直接销售,每千克可获利润12元;若粗加工后销售,每千克可获利润50元;若精加工后销售,每千克可获利润75元.某茶叶加工厂现有这种茶叶140千克,该工厂的生产能力是:如果进行粗加工,每天可加工16千克;如果进行精加工,每天可加工6千克,但两种加工方式不能同时进行.受各种条件限制,工厂必须在15天内(含15天)将这批茶叶全部销售或加工完毕,为此该工厂营销科设计了三种方案:
24. 某种茶叶,若直接销售,每千克可获利润12元;若粗加工后销售,每千克可获利润50元;若精加工后销售,每千克可获利润75元.某茶叶加工厂现有这种茶叶140千克,该工厂的生产能力是:如果进行粗加工,每天可加工16千克;如果进行精加工,每天可加工6千克,但两种加工方式不能同时进行.受各种条件限制,工厂必须在15天内(含15天)将这批茶叶全部销售或加工完毕,为此该工厂营销科设计了三种方案:方案一:全部进行粗加工;
方案二:15天全部进行精加工,没有来得及进行精加工的利润;
方案三:将60千克进行精加工,其余的进行粗加工.
你认为选择哪种方案可获利润最多,为什么?最多可获利润多少元?