(单元测试B卷)第四章 一次函数—北师大版2023-2024学年八年级数学上册
试卷更新日期:2023-09-20 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 暑假期间,同学们打出租车去重庆欢乐谷游玩,出租车在公路上行驶了一段后,就遇上了堵车,停止不前,后来为了赶时间,出租车加快速度前往重庆欢乐谷.设同学们从上出租车开始所用的时间为自变量x,离欢乐谷的距离为因变量y.下列图象中能正确表示同学们从上出租车到抵达重庆欢乐谷整个过程中变量y与x关系的是( )A、
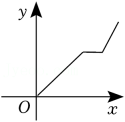 B、
B、 C、
C、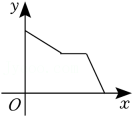 D、
D、 2. 在直角三角形ABC中, , , , 则y与x之间的函数关系式是( )A、
2. 在直角三角形ABC中, , , , 则y与x之间的函数关系式是( )A、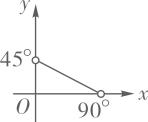 B、
B、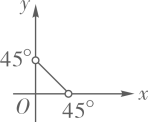 C、
C、 D、
D、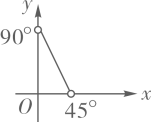 3. EF是BC的垂直平分线,交BC于点D,点A是直线EF上一动点,它从点D出发沿射线DE方向运动,当减少时,增加 , 则y与x的函数表达式是( )
3. EF是BC的垂直平分线,交BC于点D,点A是直线EF上一动点,它从点D出发沿射线DE方向运动,当减少时,增加 , 则y与x的函数表达式是( ) A、 B、 C、 D、4. 已知函数是正比例函数,则常数k的值为( )A、-2 B、0 C、2 D、±25. 直线与在同一平面直角坐标系内,其位置可能是( )A、
A、 B、 C、 D、4. 已知函数是正比例函数,则常数k的值为( )A、-2 B、0 C、2 D、±25. 直线与在同一平面直角坐标系内,其位置可能是( )A、 B、
B、 C、
C、 D、
D、 6. 已知一次函数 , 若随的增大而减小,则它的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限7. 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC , 线段PC绕点P顺时针旋转90°至线段PD , 过点D作直线AB⊥x轴,垂足为B , 直线AB与直线y=x交于点A , 且BD=2AD , 连接CD , 直线CD与直线y=x交于点Q , 则点Q的坐标为( )
6. 已知一次函数 , 若随的增大而减小,则它的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限7. 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC , 线段PC绕点P顺时针旋转90°至线段PD , 过点D作直线AB⊥x轴,垂足为B , 直线AB与直线y=x交于点A , 且BD=2AD , 连接CD , 直线CD与直线y=x交于点Q , 则点Q的坐标为( )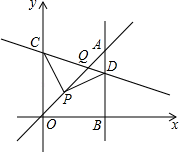 A、( , ) B、(3,3) C、( , ) D、( , )8. 在平面直角坐标系xOy中,已知直线l经过二、三、四象限,且还经过点 , , 和 , 则下列判断正确的是( )A、 B、 C、 D、9. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )
A、( , ) B、(3,3) C、( , ) D、( , )8. 在平面直角坐标系xOy中,已知直线l经过二、三、四象限,且还经过点 , , 和 , 则下列判断正确的是( )A、 B、 C、 D、9. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )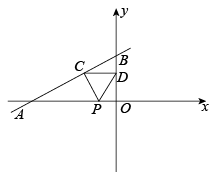 A、 B、 C、 D、10. 甲,乙两车分别从A, B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h), 甲,乙两车到B地的距离分别为y1(km), y2(km), y1 , y2关于x的函数图象如图.下列结论:①甲车的速度是 km/h;②乙车休息了0.5h;③两车相距a km时,甲车行驶了 h.正确的是( )
A、 B、 C、 D、10. 甲,乙两车分别从A, B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h), 甲,乙两车到B地的距离分别为y1(km), y2(km), y1 , y2关于x的函数图象如图.下列结论:①甲车的速度是 km/h;②乙车休息了0.5h;③两车相距a km时,甲车行驶了 h.正确的是( ) A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题(每题3分,共15分)
-
11. 如图,某链条每节长为 , 每两节链条相连接部分重叠的圆的直径为 , 按这种连接方式,x节链条总长度为 , 则y关于x的函数关系式是.
 12. 在中, , 周长为12.设 , , 则y关于x的函数表达式为.13. 如图,平面直角坐标系中,A(4,4),B为y轴正半轴上一点,连接AB,在第一象限作AC=AB,∠BAC=90°,过点C作直线CD⊥x轴于D,直线CD与直线y=x交于点E,且ED=5EC,则直线BC解析式为 .
12. 在中, , 周长为12.设 , , 则y关于x的函数表达式为.13. 如图,平面直角坐标系中,A(4,4),B为y轴正半轴上一点,连接AB,在第一象限作AC=AB,∠BAC=90°,过点C作直线CD⊥x轴于D,直线CD与直线y=x交于点E,且ED=5EC,则直线BC解析式为 .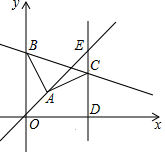 14. 如图放置的△OAB1 , △B1A1B2 , OB2A2B3都是边长为2的等边三角形,边0A在y轴上,点B1 , B2 , B3 , ……都在直线y=x上,则点A2022的坐标是
14. 如图放置的△OAB1 , △B1A1B2 , OB2A2B3都是边长为2的等边三角形,边0A在y轴上,点B1 , B2 , B3 , ……都在直线y=x上,则点A2022的坐标是 15. 如图,一次函数y=-x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为.
15. 如图,一次函数y=-x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为.
三、解答题(共4题,共20分)
-
16. 某文具店出售书包和文具盒,书包每个定价30元,文具盒每个定价5元.该店制定了两种优惠方案.
方案1:买一个书包赠送一个文具盒;
方案2:按总价的9折(总价的90%)付款.
某班学生需购买8个书包,文具盒若干(不少于8个),如果设文具盒数为x(个),付款数为y(元).
(1)、分别求出两种优惠方案中y与x之间的关系式;(2)、购买文具盒多少个时两种方案付款相同;购买文具盒数大于8个时,两种方案中哪一种更省钱?17. 如图,广州到长沙700km,现有一列高铁从长沙出发,以250km/h的速度向武汉行驶.设x(h)表示高铁行驶的时间,y(km)表示高铁与广州的距离; (1)、写出y与x之间的关系式,并判断y是否为x的一次函数;(2)、当y=1050时,求x的值.18. 如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)、写出y与x之间的关系式,并判断y是否为x的一次函数;(2)、当y=1050时,求x的值.18. 如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)、求经过A,D两点的直线的函数关系式和点B的坐标;
(2)、在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P点坐标,若不存在,请说明理由.19. 甲,乙两地相距300千米.一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,线段CD对应的函数解析式是y=110x﹣195(2.5≤x≤4.5),在轿车行进过程中,轿车行驶多少时间,两车相距15千米?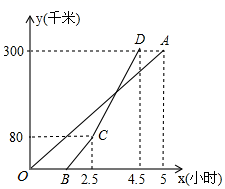
四、综合题(共4题,共35分)
-
20. 已知等腰三角形的周长为12,设腰长为x,底边长为y.(1)、试写出y关于x的函数表达式,并直接写出自变量x的取值范围.(2)、当x=5时,求出函数值.21. 已知函数.(1)、当m为何值时,这个函数是一次函数?(2)、当m为何值时,这个函数是正比例函数?22. 直线y=kx+b经过A(-2,0),B(0,4)两点,C点的坐标为(0,-1).
 (1)、求k和b的值;(2)、点E为线段AB上一点,点F为直线AC上一点,EF=3.
(1)、求k和b的值;(2)、点E为线段AB上一点,点F为直线AC上一点,EF=3.①如图1,若EFBC,求E点坐标;
②如图2,若EFAO,请直接写出E点坐标.
23. 如图1,在同一平面直角坐标系中,直线AB:与直线AC:相交于点A(m,4)与x轴交于点B(-4,0),直线AC与x轴交于点C. (1)、填空:b= , m= , k= .(2)、如图2,点D为线段BC上一动点,将△ACD沿直线AD翻折得到△AED,线段AE交x轴于点F.
(1)、填空:b= , m= , k= .(2)、如图2,点D为线段BC上一动点,将△ACD沿直线AD翻折得到△AED,线段AE交x轴于点F.①当点E落在y轴上时,求点E的坐标.
②若△DEF为直角三角形,求点D的坐标.