云南省昆明市官渡区2022-2023学年七年级下学期期末数学试卷

试卷更新日期：2023-09-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题只有一个正确选项，每小题3分，共36分）

1. 官渡区的区标包含如图的飞马形象，下列四个选项中能由图平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各项调查中，更适合全面调查的是（）

A、某校七（1）班学生最喜欢的学科 B、端午节最受欢迎粽子的口味 C、某品牌电视机的使用寿命 D、昆明市初中学生的课外活动时间

查看试题解析
3. 把方程2x-y＝3改写成用含x的式子表示y的形式，正确的是（）

A、y＝2x+3 B、y＝2x-3 C、 $y = \frac{1}{2} x + \frac{3}{2}$ D、 $y = \frac{1}{2} x - \frac{3}{2}$

查看试题解析
4. 已知a＜b，下列不等式变形中正确的是（）

A、a-2＞b-2 B、 $\frac{a}{3} > \frac{b}{3}$ C、-2a＞-2b D、5a+2＞5b+2

查看试题解析
5. 下列命题是真命题的是（）

A、相等的两个角是对顶角 B、过直线外一点有且只有一条直线与已知直线平行 C、两条直线被第三条直线所截，同位角相等 D、从直线外一点到这条直线的垂线段，叫做这点到直线的距离

查看试题解析
6. 若点M（m+2，-1）在第四象限，则m的取值范围是（）

A、-2＜m＜0 B、m＜-2 C、m＞0 D、m＞-2

查看试题解析
7. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益部游戏．如图是一局象棋残局，已知表示棋子“马“和“車”的点的坐标分别为（4，3），（-2，1），则表示棋子“炮”的点的坐标为（）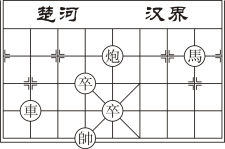

A、（2，3） B、（2，1） C、（1，2） D、（1，3）

查看试题解析
8. 如图，点E在AC的延长线上，下列条件中不能判断BD∥AC的是（）

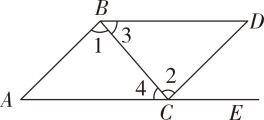A、∠1＝∠2 B、∠3＝∠4 C、∠D＝∠DCE D、∠D+∠ACD＝180°

查看试题解析
9. 光线在不同介质中的传播速度是不同的，因此光线从水中射向空气时，要发生折射．由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图，若平行光线由水中射向空气时所形成的∠1＝50°，∠2＝113°，则∠3+∠4为（）

A、90° B、107° C、117° D、163°

查看试题解析
10. 直角三角板ABC与直角三角板DEF如图摆放，其中∠BAC＝∠EDF＝90°，∠E＝45°，∠C＝30°，AC与DE相交于点M．若BC∥EF，则∠CME为（）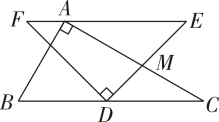

A、45° B、55° C、65° D、75°

查看试题解析
11. 若不等式（a-2）x＞4的解集为 $x < \frac{4}{a - 2}$ ，则a的取值范围是（）

A、a＜2 B、a＞2 C、a≥2 D、a≤2

查看试题解析
12. 如图，在平面直角坐标系中，半径均为1个单位长度的半圆O₁ ，半圆O₂ ，半圆O₃ ，半圆O₄ ， …，组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒 $\frac{π}{2}$ 个单位长度，则第2035秒时，点P的坐标是（）

A、（2035，-1） B、（2035，0） C、（2036，0） D、（2036，-1）

查看试题解析

二、填空题（本大题共4小题，每小题2分，共8分）

13. 已知一个正数的两个不同的平方根分别是2a+1和3-4a，则a＝．

查看试题解析
14. 已知x，y满足方程组 ${\begin{array}{l} 2 x + 3 y = 3 \\ 3 x + 2 y = 7 \end{array}$ ，则2023+x+y＝．

查看试题解析
15. 如图，直线AB、CD相交于点O，OE平分∠AOD，OF⊥CD于点O，若∠AOE＝65°，则∠BOF的度数是．

查看试题解析
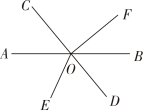16. 已知关于x，y的二元一次方程a₁x+b₁y＝c₁的部分解如表：

x

…

-1

2

5

8

11

…

y

…

-19

-12

-5

2

9

…

关于x，y的二元一次方程a₂x+b₂y＝c₂的部分解如表：

x

…

-1

2

5

8

11

…

y

…

-70

-46

-22

2

26

…

则关于x，y的二元一次方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解是．

查看试题解析

三、解答题（本大题共8小题，共56分）

17. 计算： $(- 1)^{2024} - \sqrt[3]{8} + \sqrt{(- 2)^{2}} - | 1 - \sqrt{2} |$

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} x - y = 1 \\ x + y = - 4 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x + 2 y = 8 \\ 2 x - y = 3 \end{array}$ ．

查看试题解析
19. 解不等式组 ${\begin{array}{l} 2 (x - 1) ⩽ 3 x - 1 \\ \frac{x + 1}{2} - 1 < \frac{x}{3} \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析

20. 2020年云南省开始中考体育改革，把体育成绩按100分计入中考总分，每学期都要进行体育测试．为了解我区七年级11000名学生下学期的体育成绩，随机抽查了我区七年级部分学生下学期的体育成绩，发现样本中的成绩均不少于60分，绘制不完整的统计图表：

七年级下学期的体育成绩频数分布表：

组别	1	2	3	4
分数段	60≤x＜70	70≤x＜80	80≤x＜90	90≤x≤100
频数	20	a	150	230
百分比	4%	20%	b	c%

七年级下学期的体育成绩频数分布直方图：

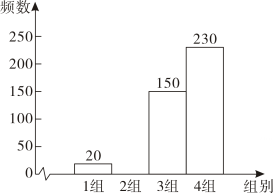(1)、通过计算确定频数分布表中a，b，c的值；

(2)、补全频数分布直方图；

(3)、若分数不小于80分，记为“A”，估计我区七年级下学期体育成绩记为“A”的学生有多少人．

查看试题解析

21. 如图，已知AD⊥BC于点D，EF⊥BC于点F，∠1+∠2＝180°，证明：∠CGD＝∠CAB．请补全证明过程．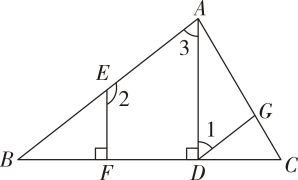

证明：∵AD⊥BC，EF⊥BC（已知），

∴∠ADB＝ ▲ ＝90°（垂直的定义），

∴AD∥ ▲ （同位角相等，两直线平行），

∴ ▲ +∠2＝180°（），

∵∠1+∠2＝180°（已知），

∴ ▲ ＝∠1（同角的补角相等），

∴DG∥ ▲ （），

∴∠CGD＝∠CAB（两直线平行，同位角相等）．

查看试题解析
22. 昆明的蓝花楹在4月中下旬陆续绽放，引来众多游客踏青观赏，拍照留念：小渡计划购进A、B两种型号的手机自拍杆进行销售，已知购进1个A型号和2个B型号的自拍杆共需75元，购进2个A型号和3个B型号的自拍杆共需120元．

(1)、求购进A型号自拍杆和B型号自拍杆的单价分别是多少元？

(2)、若小渡计划购进A，B两种型号的自拍杆共100个，并将A，B两种型号的自拍杆分别以20元/个，50元/个售出，为了保证全部售完后的总利润不低于1100元，最多购进A型号的自拍杆多少个？

查看试题解析
23. 无理数是无限不循环小数，因此无理数的小数部分不可能全部写出来．
材料一：估算法确定无理数的小数部分
∵ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$
∴ $\sqrt{7}$ 的整数部分为2，
∴ $\sqrt{7}$ 的小数部分为 $\sqrt{7} - 2$ ；
材料二：面积法求一个无理数的近似值，
已知面积为5的正方形的边长是 $\sqrt{5}$ ，
∵ $2 < \sqrt{5} < 3$ ，
∴设 $\sqrt{5} = 2 + x$ （x为 $\sqrt{5}$ 的小数部分，0＜x＜1）．
画出示意图：由图可知，正方形的面积由四个部分组成，S_正方形＝x²+2•x+2•x+4，
∵S_正方形＝5，
∴x²+2•x+2•x+4＝5
略去x² ，得方程4•x+4＝5，解得：x＝0.25，即 $\sqrt{5} \approx 2.25$ ，
解决问题：

(1)、结合你所学的知识，探究 $\sqrt{10}$ 的近似值（结果精确到0.01）；

(2)、请总结估算 $\sqrt{n}$ （n为开方开不尽的数）的一般方法．

查看试题解析
24. 如图，已知点A（a，0），B（b，0）满足（4a+b）²+|b-4|＝0．将线段AB先向上平移4个单位，再向右平移1个单位后得到线段CD，连接AC，BD．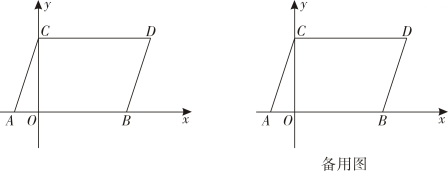

(1)、直接写出点A和点B的坐标；

(2)、点M从O点出发，以每秒1个单位的速度向上平移运动．设运动时间为t秒，当t为多少时，四边形OMDB的面积等于10？

(3)、在（2）的条件下，点M从O点出发的同时，点N从B点出发，以每秒 $\frac{5}{4}$ 个单位的速度向左平移运动，设射线DN交y轴于点E．在运动过程中S_△EMD-S_△OEN的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．

查看试题解析

x	…	-1	2	5	8	11	…
y	…	-19	-12	-5	2	9	…

x	…	-1	2	5	8	11	…
y	…	-70	-46	-22	2	26	…