吉林省长春市汽开区2022-2023学年七年级下学期期末数学试卷

试卷更新日期：2023-09-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分）

1. 在实数0， $\sqrt{2}$ ， $\frac{1}{7}$ ， -3中，无理数是（）

A、0 B、 $\sqrt{2}$ C、 $\frac{1}{7}$ D、-3

查看试题解析
2. 不等式2x-1＜3x+1的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
3. 下列分别表示“节水”、“节能”、“回收”、“绿色食品”含义的四个标志的图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 用代入法解方程组 ${\begin{array}{l} y = 1 - x \\ x - 2 y = 4 \end{array}$ ，将第一个方程代入第二个方程正确的是（）

A、x-2+2x＝4 B、x-2-2x＝4 C、x-2-x＝4 D、x-2+x＝

查看试题解析
5. 正十边形的内角和度数为（）

A、360° B、720° C、1440° D、1800°

查看试题解析
6. 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（）

A、60° B、120° C、60°或120° D、30°或150°

查看试题解析
7. 下列四个结论中，正确的是（）

A、3.15＜ $\sqrt{10}$ ＜3.16 B、3.16＜ $\sqrt{10}$ ＜3.17 C、3.17＜ $\sqrt{10}$ ＜3.18 D、3.18＜ $\sqrt{10}$ ＜3.19

查看试题解析
8. 我国明代数学家程大位所著《算法统宗》中记载了一道有趣的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”题目大意是：100个和尚分100个馒头，刚好分完．大和尚1人分3个馒头，小和尚3人分一个馒头．问大、小和尚各有多少人？若大和尚有x人，小和尚有y人．则下列方程或方程组中，正确的有（）
① ${\begin{array}{l} x + y = 100 \\ \frac{1}{3} x + 3 y = 100 \end{array}$ ；② ${\begin{array}{l} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{array}$ ；③3x+ $\frac{1}{3}$ （100-x）＝100；④ $\frac{1}{3}$ y+3（100-y）＝100．

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分)

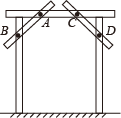
9. 64的平方根是．

查看试题解析
10. 若一个三角形两边长分别为2、5，则此三角形的周长c的取值范围为．

查看试题解析
11. 如图所示，王师傅做完门框为防止变形，在门上钉上AB、CD两条斜拉的木条，其中的数学原理是．

查看试题解析
12. 如图是一个旋转对称图形，要使它旋转后与自身重合，应将它绕中心逆时针方向旋转的度数至少为°．

查看试题解析
13. 如图，△ABC≌△A'B'C'，其中∠A＝35°，∠B'＝120°，则∠C的大小为度．

查看试题解析
14. 如图，用正多边形镶嵌地面，则图中α的大小为度．

查看试题解析

三、解答题（本大题共10小题，共78分）

15.

(1)、解方程：3（x-1）＝5x+11．

(2)、解不等式：2x＜4x+8．

查看试题解析
16. 解方程组： ${\begin{array}{l} 2 x - y = 4 \\ x + 3 y = 9 \end{array}$ ．

查看试题解析
17. 解不等式组 ${\begin{array}{l} 4 x > 2 x - 6 \\ \frac{x - 1}{3} ⩽ \frac{x + 5}{9} \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
18. 已知一个多边形的内角和比外角和多720°，求这个多边形的每个内角度数与边数n ．

查看试题解析
19. 图①、图②均是10×10的正方形网格，每个小正方形的边长均为1，其顶点称为格点，△ABC的顶点均在格点上．只用无刻度的直尺，在给定的网格中按要求作图，保留适当的作图痕迹．

(1)、在图①中，将△ABC向右平移，使点A与点A₁重合，画出△A₁B₁C₁ ．

(2)、在图②中，画出△ABC关于点O的中心对称图形△A₂B₂C₂ ．

(3)、△ABC的面积为．

查看试题解析
20. 如图，在△ABC中，AD是BC边上的中线，AF是BC边上的高线，点E为AD的中点．

(1)、若∠ABE＝27°，∠BAD＝35°，求∠BED的度数．

(2)、若△BDE的面积为10，CD＝5，求AF的长．

查看试题解析

21. 观察表格回答下列问题：

a	…	0.0001	0.01	1	100	10000	…
$\sqrt{a}$	…	0.01	x	1	y	100	…

(1)、表格中x＝， y＝．

(2)、从表格中探究a与

\sqrt{a}

数位之间的变化规律，并利用规律解决下面问题：

①已知 $\sqrt{10} \approx 3.16$ ，则 $\sqrt{1000} \approx$ ．

②已知 $\sqrt{2.56} = 1.6$ ，若 $\sqrt{a} = 160$ ，则a＝．

查看试题解析

22. 随着网上购物日渐流行，某快递公司为提高工作效率采用机器人分拣包裹．该公司采用A、B两种型号机器人，若A型机器人工作2小时，B型机器人工作3小时，则一共可以分拣680件包裹；若A型机器人工作3小时，B型机器人工作2小时，则一共可以分拣720件包裹．

(1)、问A、B两种型号机器人每小时各分拣多少件包裹？

(2)、“6•18”期间，快递公司的业务量猛增，要让A、B型机器人每天分拣包裹的总量不低于3080件，问它们每天至少要一起工作多少小时？

查看试题解析
23. 实践与探究
材料：一副直角三角尺，记作：△ABC和△DEF ，其中∠ACB＝∠EFD＝90°，∠BAC＝30°，∠DEF＝45°．

(1)、操作一：如图①，将三角尺按如图摆放，其中点C、D、A、F在同一条直线上，另两条直角边所在的直线分别为MN、PQ ， AB与DE相交于点O ，则∠BOE的大小为度．

(2)、操作二：保持MN、PQ不变，将图①中的三角尺经过适当平移旋转，得到的位置如图②所示，点B在MN上，点F在PQ上，点A与点E重合，点C与点D重合，且BA平分∠MBC ，求∠PFA的度数．

(3)、操作三：如图③，将图①位置的三角尺ABC绕点B顺时针旋转一周，速度为每秒10°，设运动时间为t秒，当边AB与DE互相平行时，直接写出t的值．

查看试题解析
24. 如图，在长方形ABCD中，AB＝3，BC＝4．点P从点A出发，沿折线AB-BC以每秒2个单位的速度向点C运动，同时点Q从点C出发，沿CB以每秒1个单位的速度向点B运动，当点P到达点C时，点P、Q同时停止运动．设点P的运动时间为t秒．

(1)、当点P在AB边上运动时，PB＝；当点P在BC边上运动时，PB＝（用含t的代数式表示）

(2)、当点P与点Q重合时，求t的值．

(3)、当t＝1时，求△PDQ的面积．

(4)、若点P关于点B的中心对称点为点P′，直接写出△PDP'和△QDC面积相等时t的值．

查看试题解析