吉林省长春市二道区2022-2023学年七年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共8道小题,每小题3分,共24分)
-
1. 下列漂亮的图案中既是中心对称图形又是轴对称图形的是( )A、
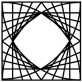 B、
B、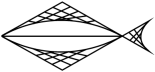 C、
C、 D、
D、 2. 现有长度分别为10cm和20cm的两根小棒,王红要从下面四种长度的小棒中选取其中一根小棒拼成三角形,则她所选择的小棒是( )A、5cm B、25cm C、35cm D、40cm3. 不等式组的解集在数轴上表示正确的是( )A、
2. 现有长度分别为10cm和20cm的两根小棒,王红要从下面四种长度的小棒中选取其中一根小棒拼成三角形,则她所选择的小棒是( )A、5cm B、25cm C、35cm D、40cm3. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、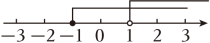 C、
C、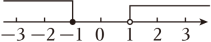 D、
D、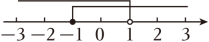 4. 李明同学在学完用正多边形拼地板这节课之后,建议爸爸为他家房屋地面进行装修.爸爸选中了一种漂亮的正八边形地砖,他告诉爸爸,只用一种八边形地砖是不能铺满地面的,但可以与另外一种边长相等的正多边形地砖组合使用,你认为要使地面铺满,李明应建议爸爸选择另一种地砖的形状为( )A、正三角形 B、正方形 C、正五边形 D、正六边形5. 下列方程变形正确的是( )A、由x+3=y-7,得x+7=y-11 B、由7y-6=5-2y,得7y+6=17-2y C、由7x=-7x,得1=-1 D、由4x=3-2x,得4x-2x=36. 如图,△ABC的周长为12cm,若将△ABC沿射线BC方向平移3cm后得到△DEF,AC与DE相交点G,连结AD,则△ADG与△ECG的周长和为( )
4. 李明同学在学完用正多边形拼地板这节课之后,建议爸爸为他家房屋地面进行装修.爸爸选中了一种漂亮的正八边形地砖,他告诉爸爸,只用一种八边形地砖是不能铺满地面的,但可以与另外一种边长相等的正多边形地砖组合使用,你认为要使地面铺满,李明应建议爸爸选择另一种地砖的形状为( )A、正三角形 B、正方形 C、正五边形 D、正六边形5. 下列方程变形正确的是( )A、由x+3=y-7,得x+7=y-11 B、由7y-6=5-2y,得7y+6=17-2y C、由7x=-7x,得1=-1 D、由4x=3-2x,得4x-2x=36. 如图,△ABC的周长为12cm,若将△ABC沿射线BC方向平移3cm后得到△DEF,AC与DE相交点G,连结AD,则△ADG与△ECG的周长和为( )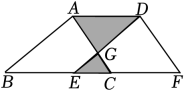 A、15cm B、13cm C、12cm D、9cm7. 如图,将一副三角板重叠,使两个直角顶点重合,若两直角重叠形成的角∠BAE=72°,则图中∠α的度数为( )
A、15cm B、13cm C、12cm D、9cm7. 如图,将一副三角板重叠,使两个直角顶点重合,若两直角重叠形成的角∠BAE=72°,则图中∠α的度数为( )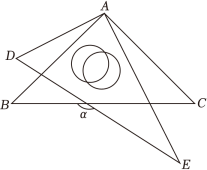 A、108° B、120° C、145° D、147°8. 我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两.问客人有几人?设客人有x人,则可列方程为( )A、7x+4=9x-8 B、7x-4=9x+8 C、 D、
A、108° B、120° C、145° D、147°8. 我国明代数学读本《算法统宗》中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两.问客人有几人?设客人有x人,则可列方程为( )A、7x+4=9x-8 B、7x-4=9x+8 C、 D、二、填空题(本大题共6道小题,每小题3分,共18分)
-
9. 已知关于x的方程2x+a-3=0的解是x=-1,则a的值为 .10. 若将二元一次方程3x-y=5写成用含x的代数式表示y的形式,则y= .11. 若关于x,y的二元一次方程组的解x,y满足x+y>1,则满足题意的最小整数a是 .12. 如图,已知△ABC≌△DBC,∠ABC=60°,∠ACD=50°,那么∠D=度.
 13. 如图,等边△ABC的每个内角都等于60°,点D是边AB上的点,连结CD,将△CDB沿CD折叠,点B的对应点为点B',连结B′D.若∠BCB'=90°,B′D交AC于点E,则∠AEB'=度.
13. 如图,等边△ABC的每个内角都等于60°,点D是边AB上的点,连结CD,将△CDB沿CD折叠,点B的对应点为点B',连结B′D.若∠BCB'=90°,B′D交AC于点E,则∠AEB'=度.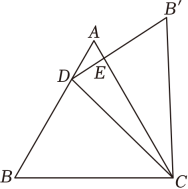 14. 如图,在△ABC中,点D、E、F分别是BC、AD、BE的中点.若△ABC的面积为10cm2 , 则△FBC的面积为cm2 .
14. 如图,在△ABC中,点D、E、F分别是BC、AD、BE的中点.若△ABC的面积为10cm2 , 则△FBC的面积为cm2 .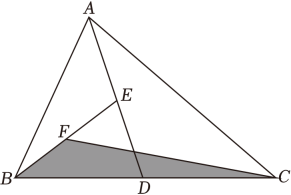
三、解答题(本大题共10小题,共78分)
-
15. 解方程组 .16. 解方程: .17. 下面是张莉同学解不等式的过程,请认真阅读并完成相应任务.
解不等式: .
去分母,得24-(x-7)>8x+4.
(1)、任务一:“去分母”这一步的变形依据是____(填“A”或“B”).A、不等式两边乘(或除以)同一个正数,不等号的方向不变. B、不等式两边乘(或除以)同一个负数,不等号的方向改变.(2)、任务二:请完成上述解不等式的余下步骤,并把解集表示在数轴上.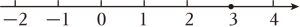 18. 已知一个多边形的内角和比它的外角和的3倍多 .(1)、求这个多边形是几边形;(2)、如果从这个多边形的一个顶点引出对角线,最多可以引条对角线.19. 如图,在直角三角形ABC中,CD是斜边AB上的高,∠BCD=35°,求:
18. 已知一个多边形的内角和比它的外角和的3倍多 .(1)、求这个多边形是几边形;(2)、如果从这个多边形的一个顶点引出对角线,最多可以引条对角线.19. 如图,在直角三角形ABC中,CD是斜边AB上的高,∠BCD=35°,求: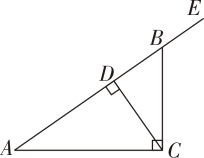 (1)、∠EBC的度数;(2)∠A的度数.
(1)、∠EBC的度数;(2)∠A的度数.对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
解:(1)CD⊥AB(已知),
∴∠CDB= ▲ .
∵∠EBC=∠CDB+∠BCD ▲ ,
∴∠EBC= ▲ +35°= ▲ (等量代换)(2)∵∠EBC=∠A+∠ACB( )
∴∠A=∠EBC-∠ACB(等式的性质)
∵∠ACB=90°(已知),
∴∠A= ▲ -90°= ▲ (等量代换).
你还能用其他方法解决这一问题吗?
20. 图①、图②、图③都是4×4的正方形网格,每个小正方形顶点叫做格点.△ABC的顶点A、B、C均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图.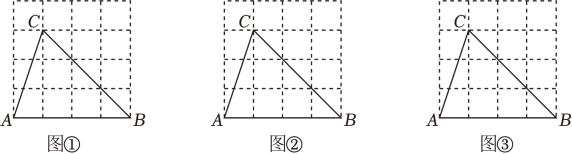 (1)、在图①中作△ABC边AB上的高CD.(2)、在图②中作△ABC边BC上的高AE.(3)、在图③中作△ABC边AC上的高BF.21. 阅读下列材料,解答下面的问题.
(1)、在图①中作△ABC边AB上的高CD.(2)、在图②中作△ABC边BC上的高AE.(3)、在图③中作△ABC边AC上的高BF.21. 阅读下列材料,解答下面的问题.我们知道每一个二元一次方程都有无数组解,例如……都是方程x+2y=5的解,但在实际生活中我们往往只需求出其正整数解即可.
我们在求一个二元一次方程的正整数解时通常采用如下方法:
例:求2x+5y=24这个二元一次方程的正整数解.
解:由2x+5y=24,得: ,
根据x、y为正整数,运用尝试法可以知道
方程2x+5y=24的正整数解为 或 .
问题:
(1)、若为非负整数,则满足条件的整数x的值有个.(2)、直接写出满足方程2x+3y=8的正整数解 _(3)、若要把一根长为32m的绳子截成长为3m和4m两种规格的绳子若干段(两种规格都有),请你在不浪费材料的情况下,通过计算来设计几种不同的截法.22. 如图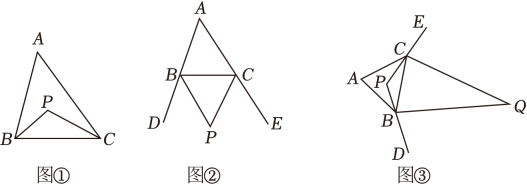 (1)、【探索发现】在一次数学学习活动中,刘华遇到了下面的这个问题:
(1)、【探索发现】在一次数学学习活动中,刘华遇到了下面的这个问题:如图①,在△ABC中,BP平分∠ABC,CP平分∠ACB,请你判断∠A和∠P间的数量关系并说明理由.
刘华对这个问题进行了判断并给出了证明过程,下面是部分证明过程,请你补全余下的证明过程.
解:结论:∠P=_ .
理由:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB.
∴∠P=180°-∠PBC-∠PCB.
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=_
(2)、【模型发展】如图②,点P是△ABC的外角平分线BP与CP的交点,请你判断∠A和∠P间的数量关系并说明理由.(3)、【解决问题】如图③,在△ABC中,BP平分∠ABC,CP平分∠ACB,点Q是△PBC的外角平分线BQ与CQ的交点.若∠A=68°,则∠Q=_度.23. 某学校七年级甲、乙两班为丰富学生的体育活动购买了一批足球和篮球,足球和篮球的价格不同,如图是两个班级购买的足球和篮球的数量及消费的金额. (1)、求每个足球和篮球的价格.(2)、若该校七年级丙班在同一商场购买了同种型号的足球3个、篮球1个,则该班共消费 元.(3)、若该校八年级在同一商店采购同种型号的足球和篮球共10个,且他们的消费金额不少于460元,则该校八年级至少购买了多少个足球?24. 如图,在长方形ABCD中,AB=6cm,BC=4cm,点P从点A出发,以每秒4cm的速度沿折线AB一BC运动,同时点Q从点C出发,以每秒1.5cm的速度沿射线CB方向运动,当点P到达终点C时,点Q随之停止运动.设点P的运动时间为t(秒).
(1)、求每个足球和篮球的价格.(2)、若该校七年级丙班在同一商场购买了同种型号的足球3个、篮球1个,则该班共消费 元.(3)、若该校八年级在同一商店采购同种型号的足球和篮球共10个,且他们的消费金额不少于460元,则该校八年级至少购买了多少个足球?24. 如图,在长方形ABCD中,AB=6cm,BC=4cm,点P从点A出发,以每秒4cm的速度沿折线AB一BC运动,同时点Q从点C出发,以每秒1.5cm的速度沿射线CB方向运动,当点P到达终点C时,点Q随之停止运动.设点P的运动时间为t(秒).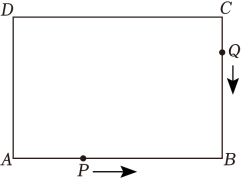 (1)、①当点P在AB上运动时,BP=cm.(用含t的代数式表示)
(1)、①当点P在AB上运动时,BP=cm.(用含t的代数式表示)②当点P在BC上运动时,BP=cm.(用含t的代数式表示)
(2)、当点P运动到BC的中点时,求线段BQ的长.(3)、当点P与点Q到点B的距离相等时,求t的值.(4)、当点P在BC上运动时,连结AP、AQ.直接写出△APQ的面积是3cm2时t的值.