吉林省长春市宽城区2022-2023学年八年级下学期期末数学试卷

试卷更新日期：2023-09-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）

1. 二次根式 $\sqrt{x + 3}$ 有意义时， $x$ 的取值范围是（）

A、 $x \geq - 3$ B、 $x > - 3$ C、 $x \leq - 3$ D、 $x \neq - 3$

查看试题解析
2. 在平面直角坐标系中，点 $P (- 3 ， m^{2} + 1)$ 关于原点对称点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $(- 2 ， 3)$ ，则它的图象也一定经过的点是（）

A、 $(6 ， 1)$ B、 $(1 ， - 6)$ C、 $(- 3 ， - 2)$ D、 $(- 2 ， - 3)$

查看试题解析
4. 某校开展安全知识竞赛，进入决赛的学生有 $20$ 名，他们的决赛成绩如表所示：
决赛成绩 $/$ 分
          $100$
          $99$
          $98$
          $97$
人数
     $3$
     $7$
     $6$
     $4$
则这 $20$ 名学生决赛成绩的中位数和众数分别是（）

A、 $98$ ， $98$ B、 $98$ ， $99$ C、 $98.5$ ， $98$ D、 $98.5$ ， $99$

查看试题解析
5. 在平面直角坐标系中，点 $A (\frac{3}{2} ， m)$ 、 $B (\frac{\sqrt{7}}{2} ， n)$ 是直线 $y = k x + b (k > 0)$ 上的两点，则 $m$ 、 $n$ 的大小关系是（）

A、 $m > n$ B、 $m < n$ C、 $m \geq n$ D、 $m \leq n$

查看试题解析
6. 如图，矩形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O .$ 若 $∠ A O D = 120 °$ ， $A C = 4$ ，则 $C D$ 的长为（）

A、 $1$ B、 $2$ C、 $2 \sqrt{3}$ D、 $3$

查看试题解析
7. 如图，在菱形ABCD中，M，N分别在AB，CD上，且AM＝CN，MN与AC交于点O，连接BO．若∠DAC＝28°，则∠OBC的度数为（　　）

A、28° B、52° C、62° D、72°

查看试题解析
8. 如图，在平面直角坐标系中， $O$ 为坐标原点，▱ $O A B C$ 的顶点 $A$ 在函数 $y = - \frac{4}{x} (x > 0)$ 的图象上，点 $C$ 在函数 $y = \frac{k}{x} (x > 0 ， k > 0)$ 的图象上，若点 $A$ 、 $B$ 的横坐标分别为 $2$ 、 $6$ ，则 $k$ 的值为（）

A、 $4$ B、 $6$ C、 $8$ D、 $12$

查看试题解析

二、填空题（本大题共6小题，共18.0分）

9. $\sqrt{12} \div \sqrt{3} =$ ．

查看试题解析
10. 在平面直角坐标系中，若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $(- 1 ， 2)$ ，则一次函数 $y = k x + 2$ 的图象一定不经过第象限．

查看试题解析
11. 在平面直角坐标系中，一次函数 $y = 3 x - 1$ 与 $y = k x (k \neq 0)$ 的图象的交点坐标是 $(1 ， 2)$ ，则方程组 ${\begin{array}{l} 3 x - y = 1 \\ k x - y = 0 \end{array}$ 的解是．

查看试题解析
12. 如图，菱形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，若 $A B = 2 \sqrt{5} cm$ ， $A C = 4 cm$ ，则 $B D$ 的长为cm.

查看试题解析
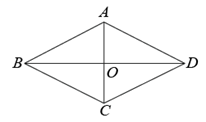13. 如图，在平面直角坐标系中， $O$ 为坐标原点，正方形 $O A B C$ 的顶点 $A$ 的坐标为 $(1 ， \sqrt{3})$ ，点 $B$ 为第二象限的点，则点 $B$ 的纵坐标为．

查看试题解析
14. 如图，在 $▱ A B C D$ 中，点E在 $A D$ 上，且 $E C$ 平分 $∠ B E D$ ，若 $∠ E B C = 30 °$ ， $B E = 10$ ，则 $▱ A B C D$ 的面积为.

查看试题解析

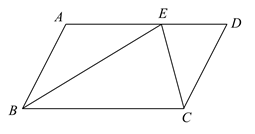
三、解答题（本大题共10小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）

15. 计算： $(2 \sqrt{5} - 3) (3 \sqrt{5} + 2)$ ．

查看试题解析
16. 如图，在平面直角坐标系中，点 $A$ 在第一象限内， $A B ⊥ x$ 轴于点 $B$ ，函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象分别交 $O A$ 、 $A B$ 于点 $C$ 、 $D .$ 已知点 $C$ 的坐标为 $(2 ， 2)$ ， $B D = 1$ ．

(1)、求 $k$ 的值及点 $D$ 的坐标．

(2)、已知点 $P$ 在该函数的图象上，且在 $△ A O B$ 的内部，直接写出点 $P$ 的横坐标 $x$ 的取值范围．

查看试题解析
17. 如图，在▱ $A B C D$ 中， $D E ⊥ A B$ 于点 $E$ ， $B F ⊥ A B$ 交 $C D$ 于点 $F$ ．
求证：四边形 $D E B F$ 是矩形．

查看试题解析
18. 图 $①$ 、图 $②$ 、图 $③$ 均是 $6 \times 6$ 的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为 $1$ ，点 $A$ 、 $B$ 均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上．

(1)、在图 $①$ 中，以 $A B$ 为边画一个▱ $A B C D$ ，且其面积为 $4$ ；

(2)、在图 $②$ 中，以 $A B$ 为对角线画一个▱ $A E B F$ ，且其面积为 $4$ ；

(3)、在图 $③$ 中，以 $A B$ 为对角线画一个▱ $A M B N$ ，且其面积为 $5$ ．

查看试题解析
19. 如图，在平面直角坐标系中，点 $A (m ， 3)$ 在函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上，点 $B$ 在 $y$ 轴上， $O B = 1$ ，将线段 $A B$ 向右下方平移，得到线段 $C D$ ，此时点 $C$ 落在函数 $y = \frac{k}{x}$ 的图象上，点 $D$ 落在 $x$ 轴正半轴上，且 $O D = 1$ ．

(1)、求 $k$ 的值；

(2)、求直线 $A C$ 所对应的函数表达式．

查看试题解析
20. 如图，在矩形 $A B C D$ 中，点 $E$ 在对角线 $A C$ 上，点 $F$ 在边 $C D$ 上 $($ 点 $F$ 与点 $C$ 、 $D$ 不重合 $)$ ， $B E ⊥ E F$ ， $∠ A B E + ∠ C E F = 45 °$ ．

(1)、求 $∠ 1 + ∠ 2$ 的度数；

(2)、求证：四边形 $A B C D$ 是正方形．

查看试题解析
21. 某校举办“科创达人”比赛，比赛分为笔试和科创作品展示两部分，其中笔试成绩占40%，作品展示成绩占60%．作品展示由十位评委现场打分后取平均数．对参加比赛的甲、乙两位同学得分数据进行整理、描述和分析，下面给出了部分信息．
a ．甲、乙两位同学的笔试成绩分别为85分、90分．

b ．甲同学作品展示十位评委给分的部分折线图：

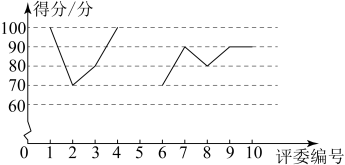
c ．乙同学作品展示十位评委给分：

80，90，90，80，80，80，70，80，70，80．

d．甲、乙同学作品展示十位评委给分的平均数：

同学

甲

乙

平均数

85

m

根据以上信息，回答下列问题：

(1)、补全甲同学作品展示评委给分折线统计图；

(2)、 $m =$ ；

(3)、科创作品展示中，如果某同学得分的10个数据的方差越小，则认为评委对该同学的作品评价越一致．据此判断：在甲、乙两位同学中，评委对的评价更一致（填“甲”或“乙”）：

(4)、通过计算说明甲、乙两位同学中哪位同学的总成绩较高．

查看试题解析
22. 甲、乙两车同时从 $A$ 地出发沿同一线路前往 $B$ 地 $.$ 甲车匀速行驶 $2$ 小时后，收到紧急通知，立即提高速度匀速前往 $B$ 地，比乙车提前 $1$ 小时到达 $B$ 地 $.$ 设甲、乙两车各自距 $A$ 地的路程为 $y ($ 千米 $)$ ，乙车行驶的时间为 $x ($ 时 $)$ ， $y$ 与 $x$ 之间的部分函数图象如图所示．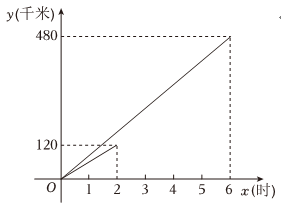

(1)、乙车每小时行驶的路程为千米；

(2)、补全甲车提高速度后的函数图象，并求出提高速度后甲车距 $A$ 地的路程 $y$ 与 $x$ 之间的函数关系式；

(3)、求甲、乙两车相遇时，甲车距 $A$ 地的路程．

查看试题解析
23.

(1)、【感知】如图 $①$ ，将平行四边形纸片 $A B C D$ 沿过点 $D$ 的直线折叠，使点 $A$ 的对应点 $A'$ 落在边 $C D$ 上的点 $F$ 处，得到折痕 $D E$ ，点 $E$ 在边 $A B$ 上，将纸片还原，连结 $E F$ ，若 $A D = 4$ ，则四边形 $A E F D$ 的周长为．

(2)、【探究】如图 $②$ ，点 $E$ 、 $G$ 分别是平行四边形纸片 $A B C D$ 的边 $A B$ 、 $C D$ 上的点，将四边形 $A E G D$ 沿 $G E$ 折叠，点 $A$ 、 $D$ 的对应点分别为 $A'$ 、 $D'$ ，点 $A'$ 恰好落在边 $C D$ 上的点 $F$ 处，将纸片还原，连结 $A G$ 、 $E F$ ．
①求证：四边形 $A E F G$ 为菱形；
②若 $A B = 6$ ， $A D = 4$ ， $∠ B = 120 °$ ， $C F = 1$ ，则 $△ A D G$ 的面积为 ▲ ．

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = k x + b$ 与 $x$ 轴、 $y$ 轴相交于 $A (6 ， 0)$ ， $B (0 ， 3)$ 两点，动点 $C$ 在线段 $O A$ 上，将线段 $C B$ 绕着点 $C$ 顺时针旋转 $90 °$ 得到 $C D$ ，此时点 $D$ 恰好落在直线 $A B$ 上，过点 $D$ 作 $D E ⊥ x$ 轴于点 $E$ ．

(1)、求直线 $y = k x + b$ 的表达式

(2)、试确定点 $D$ 的坐标；

(3)、若点 $P$ 在 $y$ 轴上，点 $Q$ 在直线 $A B$ 上，是否存在以 $C$ ， $D$ ， $P$ ， $Q$ 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的 $Q$ 点坐标，若不存在，请说明理由．

查看试题解析

决赛成绩 $/$ 分	$100$	$99$	$98$	$97$
人数	$3$	$7$	$6$	$4$

同学	甲	乙
平均数	85	m