吉林省长春市朝阳区2022-2023学年八年级下学期期末数学试卷

试卷更新日期：2023-09-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列函数中， $y$ 是 $x$ 的正比例函数的是（）

A、 $y = x$ B、 $y = x + 1$ C、 $y = \sqrt{x}$ D、 $y = \frac{1}{x}$

查看试题解析
2. 为筹备毕业聚餐，班长对全班同学爱吃东北菜、川菜、湘菜、粤菜中的哪一种菜系的人数比较多做了民意调查 $.$ 班长做决定最关注的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
3. 互联网已经进入 $5 G$ 时代，应用 $5 G$ 网络下载一个 $1000 K B$ 的文件只需要 $0.00076$ 秒， $0.00076$ 这个数用科学记数法表示为（）

A、 $7.6 \times 1 0^{- 5}$ B、 $7.6 \times 1 0^{- 4}$ C、 $7.6 \times 1 0^{- 3}$ D、 $76 \times 1 0^{- 2}$

查看试题解析
4. 下列各点中，在 $y = x + 2$ 的函数图象上的是（）

A、 $(5 ， 3)$ B、 $(4 ， 2)$ C、 $(- 1 ， - 3)$ D、 $(1 ， 3)$

查看试题解析
5. 分式方程 $\frac{x - 1}{x + 3} = 0$ 的解是（）

A、 $x = - 3$ B、 $x = - 1$ C、 $x = 1$ D、 $x = 3$

查看试题解析
6. 如图，把矩形 $A B C D$ 沿 $E F$ 对折，若 $∠ 1 = 48 °$ ，则 $∠ A E F$ 的大小为（）

A、 $84 °$ B、 $96 °$ C、 $114 °$ D、 $132 °$

查看试题解析
7. 如图，在▱ $A B C D$ 中， $E$ 、 $F$ 是对角线 $B D$ 上的两点 $.$ 若四边形 $A E C F$ 为平行四边形，则以下三种方案中正确的方案是（）
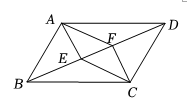
甲：只需要满足 $B F = D E$ ；
乙：只需要满足 $A E = C F$ ；
丙：只需要满足 $A E / / C F$ ．

A、甲、乙 B、甲、丙 C、乙、丙 D、甲、乙、丙

查看试题解析
8. 如图，在平面直角坐标系中，矩形 $A B C D$ 的对称轴与坐标轴重合，反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象与矩形的边分别交于点E、F、G、H，连结 $E F$ 、 $G H$ ．若 $△ A E F$ 与 $△ C G H$ 的面积和为2，且 $B E = 3 A E$ ，则k的值为（）

A、 $- 1$ B、 $- 2$ C、 $- 4$ D、 $- 8$

查看试题解析

二、填空题（本大题共6小题，共18.0分）

9. 约分 $\frac{6 x^{2} y}{2 x y}$ 的结果是．

查看试题解析
10. 甲、乙两个民族舞蹈团参加演出的女演员人数相同，平均身高相同，身高的方差分别为 $S_{甲}^{2} = 1.6$ ， $S_{乙}^{2} = 0.9$ ， $($ 填“甲”或“乙” $)$ 舞蹈团参加演出的女演员身高更整齐．

查看试题解析
11. 已知正比例函数 $y = k x$ 与反比例函数 $y = \frac{3}{x}$ 的图象没有交点，写出一个符合条件的 $k$ 的值为．

查看试题解析
12. 在▱ $A B C D$ 中，若 $∠ A$ 与 $∠ B$ 的大小的比是 $4$ ： $5$ ，则 $∠ C$ 的大小为度 $.$

查看试题解析
13. 在平面直角坐标系中，将直线 $y = - 3 x$ 向上平移 $2$ 个单位长度，平移后的直线所对应的函数表达式为．

查看试题解析
14. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为b，依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD的面积为（用含a，b的代数式表示）．

查看试题解析

三、解答题（本大题共10小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）

15. 计算： $(- 2)^{0} - | - 5 | + 3^{- 2}$ ．

查看试题解析
16. 先化简，再求值： $\frac{1}{a + 1} \times (a^{2} + a)$ ，其中 $a = - 5$ ．

查看试题解析
17. 图 $①$ 、图 $②$ 均是 $5 \times 5$ 的正方形网格，每个小正方形的边长均为 $1$ ，每个小正方形的顶点称为格点，点 $A$ 、 $B$ 均为格点 $.$ 只用无刻度的直尺，在给定的网格中，分别按照下列要求作图，保留作图痕迹．

(1)、在图 $①$ 中，以 $A B$ 为边作一个菱形 $($ 正方形除外 $)$ ，菱形的顶点是格点．

(2)、在图 $②$ 中，以 $A B$ 为对角线作一个菱形 $($ 正方形除外 $)$ ，菱形的顶点是格点．

查看试题解析
18. 某科技公司购买了一批A、B两种型号的芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用2 600元购买A型芯片的条数与用3 500元购买B型芯片的条数相等．求该公司购买B型芯片的单价．

查看试题解析
19. $2023$ 年新春伊始，中国电影行业迎来了期盼已久的火爆场面， $《$ 满江红 $》$ 、 $《$ 流浪地球 $2 》$ 、 $《$ 无名 $》$ 、 $《$ 深海 $》$ 等一大批电影受到广大影迷的青睐 $.$ 如图的统计图是其中两部电影上映后前六天的单日票房信息 $.$ 根据以上信息，回答下列问题：

(1)、1月 $22$ 日 $— 27$ 日的六天时间内，影片甲单日票房的中位数为亿元；

(2)、求 $1$ 月 $22$ 日 $— 27$ 日的六天时间内影片乙的平均日票房 $($ 精确到 $0.01$ 亿元 $)$ ；

(3)、对于甲、乙两部影片上映前六天的单日票房，下列说法中所有正确结论的序号是．
      $①$ 影片甲的单日票房逐日增加；
      $②$ 影片乙的单日票房逐日减少；
      $③$ 通过前六天的数据比较，甲单日票房的方差小于乙单日票房的方差；
      $④$ 在前六天的单日票房统计中，甲单日票房和乙单日票房之间的差值在 $1$ 月 $26$ 日达到最大．

查看试题解析
20. 如图，在平行四边形 $A B C D$ 中，连接 $B D$ ， $E$ 为线段 $A D$ 的中点，延长 $B E$ 与 $C D$ 的延长线交于点 $F$ ，连接 $A F$ ， $∠ B D F = 90 °$ ，求证：四边形 $A B D F$ 是矩形．

查看试题解析
21. 如图，小李和小赵相约去农庄游玩，小李从甲小区骑电动车出发，同时小赵从乙小区开车出发，途中去超市购物，购物后仍按原速继续驶向农庄，甲、乙小区、超市和农庄之间的路程如图 $①$ 所示，图 $②$ 中线段 $O D$ 、 $B C$ 分别表示小李、小赵行驶中离甲小区的路程 $s (k m)$ 与出发时间 $t (m i n)$ 函数图象 $($ 或部分图象 $)$
．

(1)、求线段 $B C$ 所对应的函数表达式．

(2)、请补全小赵离甲小区的路程为 $s (k m)$ 与出发时间 $t (m i n)$ 的函数图象．

(3)、直接写出小赵离开超市后，小李与小赵相距 $1 k m$ 时 $t$ 的值．

查看试题解析
22. 如图

(1)、【教材呈现】如图是华师版八年级下册数学教材第 $75$ 页练习的部分内容．
如图 $①$ ，如果直线 $l_{1} / / l_{2}$ ，那么 $△ A B C$ 的面积和 $△ D B C$ 的面积是相等的．

(2)、【方法探究】如图 $②$ ，在▱ $A B C D$ 中，点 $E$ 在边 $B C$ 上 $.$ 若 $B E = 2 E C$ ，求 $S_{△ A B E}$ 与 $S_{△ C D E}$ 数量关系．

(3)、【方法应用】如图 $③$ ，正方形 $A B C D$ 的边长为 $5$ ，点 $P$ 是正方形内部一点，连结 $A P$ 、 $B P .$ 当 $△ A B P$ 是以 $A B$ 为腰的等腰三角形，且 $S_{△ A B P} = 10$ 时，直接写出 $B P$ 的长．

查看试题解析
23. 如图，在▱ $A B C D$ 中， $A B = 12$ ， $A D = 10$ ， $D E$ 垂直平分 $A B$ 于点 $E .$ 点 $P$ 从点 $A$ 出发，沿 $A B$ 以每秒 $1$ 个单位长度的速度向终点 $B$ 运动，同时动点 $Q$ 从点 $C$ 出发沿射线 $C D$ 以每秒 $3$ 个单位长度的速度运动，点 $P$ 到达终点时， $P$ 、 $Q$ 同时停止运动 $.$ 设点 $P$ 运动的时间为 $t$ 秒 $(t > 0)$ ．

(1)、DE的长为

(2)、用含 $t$ 的代数式表示线段 $D Q$ 的长．

(3)、当以点 $A$ 、 $D$ 、 $P$ 、 $Q$ 为顶点的四边形是平行四边形时，求 $t$ 的值．

(4)、当 $△ P D Q$ 为钝角三角形时，直接写出 $t$ 的取值范围．

查看试题解析
24. 在平面直角坐标系中，直线 $l$ ： $y = k x + b (k \neq 0)$ 经过点 $A (- 2 ， 3)$ ，交 $y$ 轴于点 $B (0 ， 1)$ ．

(1)、求直线 $l$ 所对应的函数表达式．

(2)、若点 $C$ 是 $y$ 轴上一点，连结 $A C .$ 当 $△ A B C$ 的面积为 $5$ 时，求点 $C$ 的坐标．

(3)、已知线段 $M N$ 的端点坐标分别为 $M (m - 1 ， 2)$ 、 $N (\frac{1}{2} m + 3 ， 2)$ ．
$①$ 当直线 $l$ 与线段 $M N$ 有交点时，求 $m$ 的取值范围．

$②$ 已知点 $P$ 是直线 $l$ 上一点，其横坐标为 $m .$ 过点 $P$ 作直线 $l' ⊥ y$ 轴，将直线 $l$ 在直线 $l'$ 下方部分记作 $G_{1}$ ，在直线 $l'$ 上及其上方的部分记为 $G_{2}$ ，将 $G_{1}$ 沿直线 $l'$ 向上翻折得到 $G_{3}$ ， $G_{2}$ 和 $G_{3}$ 两部分组成的图象记为 $G .$ 当图象 $G$ 与线段 $M N$ 四有一个公共点时，直接写出 $m$ 的取值范围．

查看试题解析