吉林省白城市大安市三校2022-2023学年下学期八年级期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(每小题2分,共12分)
-
1. 下列根式中,是最简二次根式的是( )A、 B、 C、 D、2. 由线段 , , 组成的三角形是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 如图,在中, , 点为垂足,如果 , 则( )
 A、 B、 C、 D、4. 如图,在平面直角坐标系中,直线上一点关于轴的对称点为 , 则的值为( )
A、 B、 C、 D、4. 如图,在平面直角坐标系中,直线上一点关于轴的对称点为 , 则的值为( ) A、 B、1 C、2 D、35. 如图,在菱形中, , 的垂直平分线交对角线于点 , 垂足为 , 连接 , 则的度数是( )
A、 B、1 C、2 D、35. 如图,在菱形中, , 的垂直平分线交对角线于点 , 垂足为 , 连接 , 则的度数是( ) A、 B、 C、 D、6. 如图,点P是菱形ABCD边上的动点,它从点A出发沿A→B→C→D路径匀速运动到点D , 设 的面积为y , P点的运动时间为x , 则y关于x的函数图象大致为( )
A、 B、 C、 D、6. 如图,点P是菱形ABCD边上的动点,它从点A出发沿A→B→C→D路径匀速运动到点D , 设 的面积为y , P点的运动时间为x , 则y关于x的函数图象大致为( ) A、
A、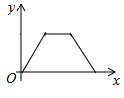 B、
B、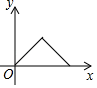 C、
C、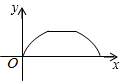 D、
D、
二、填空题(每小题3分,共24分)
-
7. 若式子 在实数范围内有意义,则x的取值范围是 .
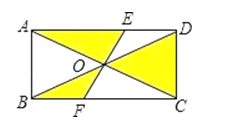
8. 甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.14 ,乙的方差是0.06 ,这5次短跑训练成绩较稳定的是(填“甲”或“乙”)9. 若直线不经过第三象限,则的取值范围是 .10.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为
 11. 已知点 , 在直线上,则、的大小关系是 .12. 如图,在中, , 是上任意一点, , , 、分别在、上,则平行四边形的周长为 .
11. 已知点 , 在直线上,则、的大小关系是 .12. 如图,在中, , 是上任意一点, , , 、分别在、上,则平行四边形的周长为 . 13. 如图,四边形和四边形都是正方形,点在上, , , 的长为 .
13. 如图,四边形和四边形都是正方形,点在上, , , 的长为 . 14. 如图,在平面直角坐标系中,点在直线上,过点作轴的平行线交直线于点 , 点均在第一象限,以为边向右作正方形 , 若 , 则点的坐标为 .
14. 如图,在平面直角坐标系中,点在直线上,过点作轴的平行线交直线于点 , 点均在第一象限,以为边向右作正方形 , 若 , 则点的坐标为 .
三、解答题(每小题5分,共20分)
-
15. 计算: .16. 如图,一次函数的图象经过、两点,与轴交于点 .
 (1)、求、的值;(2)、求的面积.17. 如图,在中, , , , 求的长.
(1)、求、的值;(2)、求的面积.17. 如图,在中, , , , 求的长. 18. 如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度 .
18. 如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度 .
四、解答题(每小题7分,共28分)
-
19. 在的网格中有线段 , 在网格线的交点上找一点 , 使三角形满足如下条件.(仅用直尺作图)
 (1)、在网格①中作一个等腰三角形;(2)、在网格②中作一个直角三角形 , 使两直角边的长为无理数.20. 学校团委组织了一次“中国梦航天情”系列活动.下面是八年级甲,乙两个班各项目的成绩(单位:分)
(1)、在网格①中作一个等腰三角形;(2)、在网格②中作一个直角三角形 , 使两直角边的长为无理数.20. 学校团委组织了一次“中国梦航天情”系列活动.下面是八年级甲,乙两个班各项目的成绩(单位:分)项目
班次
知识竞赛
演讲比赛
版面创作
甲
85
91
88
乙
90
84
87
(1)、如果根据三项成绩的平均分计算最后成绩,请通过计算说明甲、乙两班谁将获胜;(2)、如果将知识竞赛、演讲比赛、版面创作按的比例确定最后成绩,请通过计算说明甲乙两班谁将获胜.21. 如图,过点的两条直线 , 分别交轴于点 , , 其中点在原点上方,点在原点下方,已知 . (1)、求点的坐标;(2)、若的面积为4,求直线的解析式.22. 如图,在中,对角线 , 相交于点 , 点 , 分别为 , 的中点,延长至 , 使 , 连接 , .
(1)、求点的坐标;(2)、若的面积为4,求直线的解析式.22. 如图,在中,对角线 , 相交于点 , 点 , 分别为 , 的中点,延长至 , 使 , 连接 , . (1)、求证:;(2)、若 , , . 直接写出四边形的面积.
(1)、求证:;(2)、若 , , . 直接写出四边形的面积.五、解答题(每小题8分,共16分)
-
23. 如图,表示振华商场一天的某型电脑销售额与销售量的关系,表示该商场一天的销售成本与电脑销售量的关系.观察图象,解决以下问题:
 (1)、当销售量时,销售额万元,销售成本万元;(2)、一天销售台时,销售额等于销售成本;(3)、分别求出和对应的函数表达式;(4)、直接写出利润与销售量之间的函数表达式,并求出当销售量是多少时,每天的利润达到5万元?24. 如图
(1)、当销售量时,销售额万元,销售成本万元;(2)、一天销售台时,销售额等于销售成本;(3)、分别求出和对应的函数表达式;(4)、直接写出利润与销售量之间的函数表达式,并求出当销售量是多少时,每天的利润达到5万元?24. 如图
【感知】如图①,四边形、均为正方形.可知 .
(1)、【拓展】如图②,四边形、均为菱形,且 . 求证: .(2)、【应用】如图③,四边形、均为菱形,点在边上,点在延长线上.若 , , 的面积为8,则菱形的面积为 .六、解答题(每小题10分,共20分)

