云南省昆明市石林县2022-2023学年七年级下学期期末数学试卷

试卷更新日期：2023-09-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

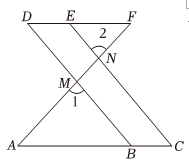
1. 下列各式中，正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $- \sqrt[3]{- 8} = - 2$ C、 $\frac{\sqrt{5} - 1}{2} < 1$ D、 $\sqrt{(- 4)^{2}} = - 4$

查看试题解析
2. 为了解某县七年级 $3650$ 名学生的视力情况，从中抽查 $200$ 名学生的视力进行统计分析，下列四个判断正确的是（）

A、 $3650$ 名学生是总体 B、样本容量是 $200$ 名 C、每名学生是总体的一个样本 D、 $200$ 名学生的视力情况是总体的一个样本

查看试题解析
3. 如果 $x > y$ ，则下列变形中正确的是（）

A、 $- \frac{1}{2} x > - \frac{1}{2} y$ B、 $\frac{1}{2} x < \frac{1}{2} y$ C、 $3 x > 5 y$ D、 $x - 3 > y - 3$

查看试题解析
4. 如图，下列不能判定 $A B / / C D$ 的条件是（）

A、 $∠ B + ∠ B C D = 180 °$ B、 $∠ 1 = ∠ 2$ C、 $∠ 3 = ∠ 4$ D、 $∠ B = ∠ 5$

查看试题解析
5. 若关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + 2 y = 1 + m \\ 2 x + y = 3 \end{array}$ 的解满足 $x - y = 5$ ，则 $m$ 的值是（）

A、 $3$ B、 $7$ C、 $- 3$ D、 $- 2$

查看试题解析
6. 在平面直角坐标系中，若点 $P (m, m + 2 ）$ 在第二象限，且m为负整数，则点P坐标为（）

A、 $(- 1, 3)$ B、 $(- 1, 1)$ C、 $(1, - 1)$ D、 $(- 2, 0)$

查看试题解析
7. 已知二元一次方程 $2 x - 7 y = 5$ ，用含 $x$ 的代数式表示 $y$ ，正确的是（）

A、 $y = \frac{2 x + 5}{7}$ B、 $y = \frac{2 x - 5}{7}$ C、 $x = \frac{5 + 7 y}{2}$ D、 $x = \frac{5 - 7 y}{2}$

查看试题解析
8. 一个数的平方根与立方根相等，则这个数是（）

A、 $0$ B、 $1$ C、 $- 1$ D、 $0$ 或 $- 1$ 或 $1$

查看试题解析
9. 下列说法：
$① \frac{23}{9}$ 是无理数； $② - 2$ 是 $4$ 的平方根； $③ \sqrt{12}$ 在两个连续整数 $a$ 和 $b$ 之间，那么 $a + b = 7$ ； $④$ 若正实数 $m$ 的平方根是 $3 a - 1$ 和 $3 a - 11$ ，则 $m = 25$ ，
其中，正确的说法有__个 $.$ （）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
10. 明代大数学家程大位著《算法统宗》一书中，记载了这样一道数学题：“八万三千短竹竿，将来要把笔头安，管三套五为期定，问都多少能完成？”用现代的话说就是：有83000根短竹，每根短竹可制成毛笔的笔管3个或笔套5个，怎样安排笔管和笔套的短竹的数量，使制成的1个笔管与1个笔套正好配套？设用于制作笔管的短竹数为x根，用于制作笔套的短竹数为y根，则可列方程为（）

A、 ${\begin{array}{l} x + y = 83000 \\ x = y \end{array}$ B、 ${\begin{array}{l} x + y = 83000 \\ 3 x = 5 y \end{array}$ C、 ${\begin{array}{l} x + y = 83000 \\ 5 x = 3 y \end{array}$ D、 ${\begin{array}{l} 3 x + 5 y = 83000 \\ x = y \end{array}$

查看试题解析
11. 若点 $M (3 ， - 2)$ 与点 $N (x$ 、 $y)$ 在同一条平行于 $x$ 轴的直线上，且 $M N = 1$ ，则 $N$ 点的坐标为（）

A、 $(4 ， - 2)$ B、 $(3 ， - 1)$ C、 $(3 ， - 1)$ 或 $(3 ， - 3)$ D、 $(4 ， - 2)$ 或 $(2 ， - 2)$

查看试题解析
12. 如图，两个一样的直角三角形重叠在一起，将其中的一个三角形沿着点 $B$ 到点 $C$ 的方向平移到 $△ D E F$ 的位置， $A B = 10$ ， $D O = 4$ ，平移距离为 $6$ ，则阴影部分面积为（）

A、 $48$ B、 $96$ C、 $21$ D、 $42$

查看试题解析

二、填空题（本大题共4小题，共8.0分）

13. 若 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是关于 $x$ 、 $y$ 的二元一次方程 $a x - 5 = y$ 的解，则 $a$ 的值为．

查看试题解析
14. 如图，已知用手盖住的点 $P$ ，到 $x$ 轴距离为 $2$ ，到 $y$ 轴的距离为 $5$ ，则 $P$ 点的坐标是．

查看试题解析
15. 若关于 $x$ 的不等式 $x - m \geq 0$ 的负整数解为 $- 1$ ， $- 2$ ， $- 3$ ，则 $m$ 的取值范围是．

查看试题解析
16. 如图，半径为 $1$ 个单位长度的圆沿数轴从实数 $- 1$ 对应的点向右滚动一周，圆上的 $A$ 点恰好与点 $B$ 重合，则点 $B$ 对应的实数是．

查看试题解析

三、解答题（本大题共8小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）

17. 解下列方程组：

(1)、 ${\begin{array}{l} y = 2 x - 3 \\ 5 x + y = 11 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x + 4 y = 2 \\ 2 x - y = 5 \end{array}$ ；

查看试题解析
18. 解不等式组 ${\begin{array}{l} 4 x + 5 \geq 2 x + 1 \\ \frac{1 + 2 x}{3} + 1 > x \end{array}$ ，并把其解集在数轴上表示出来．

查看试题解析
19. 完成下面的证明：
如图，已知： $A D ⊥ B C$ ， $F G ⊥ B C$ ，垂足分别为 $D$ 、 $G$ ，且 $∠ 1 = ∠ 2$ ，求证： $∠ B D E = ∠ C$ ．

证明： $∵ A D ⊥ B C$ ， $F G ⊥ B C ($ 已知 $)$ ，

      $∠ A D C = 90 °$ ， $∠ F G C = 90 ° ($ 垂直的定义 $)$ ，

      $∴ ∠ A D C = ∠ F G C ($ 等量代换 $)$ ，

      $∴ A D / / F G ($    $)$ ，

      $∴ ∠ 1 =$     ▲         $($    $)$ ，

又 $∵ ∠ 1 = ∠ 2 ($ 已知 $)$ ，

      $∴ ∠ 3 =$     ▲         $($    $)$ ，

      $∴ D E / / A C ($    $)$ ，

      $∴ ∠ B D E = ∠ C ($    $) .$

查看试题解析

20. 为丰富师生的校园文化生活，激发师生热爱体育运动的兴趣，增强师生体质，营造奋进、和谐的校园氛围，今年

4

月

28

日，我市某校举行了“趣味四月，神采飞扬”跳绳比赛活动

.

该校七年级采用随机抽签的方式选出了部分同学，并对这些同学一分钟跳绳的成绩进行了统计，绘制了如图统计表和统计图：

等级	次数	频数
不合格	$100 \leq x < 120$	$4$
合格	$120 \leq x < 140$	$a$
良好	$140 \leq x < 160$	$12$
优秀	$160 \leq x < 180$	$10$

根据图表中提供的信息，解答下列问题：

(1)、本次随机抽签的样本容量是；

a =

；

(2)、请补全频数分布直方图；

(3)、在扇形统计图中，“合格”等级对应的圆心角的度数是

(4)、若该校有

3000

名学生，根据抽样调查结果，请估计该校学生一分钟跳绳成绩达到良好及以上的人数．

查看试题解析

21. 如图所示的网络中， $△ A B C$ 的三个顶点均在格点上，且 $A$ 、 $B$ ，为 $A (- 5 ， - 1)$ 、 $B (1 ， 2)$ 、 $C (- 2 ， 3) .$ 现将 $△ A B C$ 平移，使点 $C$ 平移到点 $(2 ， 0)$ ，点 $A$ 、 $B$ 的对应点分别是点 $E$ 、 $F$ ．

(1)、请在图中画出 $△ A B C$ 平移后得到的 $△ E F D$ ，并写出点 $E$ 与点 $F$ 的坐标．

(2)、求 $△ A B C$ 的面积．

查看试题解析
22. 如图，点 $E$ 在 $D F$ 上，点 $B$ 在 $A C$ 上， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ ，若 $∠ A = 45 °$ ，试求 $∠ F$ 的度数．

查看试题解析
23. 在“抗疫”期间，某药店销售 $A$ 、 $B$ 两种型号的口罩，已知销售 $60$ 盒 $A$ 型和 $40$ 盒 $B$ 型的利润为 $850$ 元，销售 $30$ 盒 $A$ 型和 $50$ 盒 $B$ 型的利润为 $725$ 元．

(1)、求每盒 $A$ 型口罩和每盒 $B$ 型口罩的销售利润；

(2)、该药店计划一次购进 $A$ 、 $B$ 两种型号的口罩共 $300$ 盒，其中 $B$ 型口罩的进货量不超过 $A$ 型口罩的 $3$ 倍，且完全售出后利润不少于 $2810$ 元 $.$ 请你帮助药店老板设计一下进货方案．

查看试题解析
24. 我们定义，关于同一个未知数的不等式 $A$ 和 $B$ ，如果两个不等式的解集相同，则称不等式 $A$ 与 $B$ 为同解不等式．

(1)、若关于 $x$ 的不等式 $A$ ： $3 - 2 x > 0$ ，不等式 $B$ ： $\frac{2 x - a}{3} < 2$ 是同解不等式，求 $a$ 的值；

(2)、若关于 $x$ 的不等式 $C$ ： $x - 2 > m n$ ，不等式 $D$ ： $x - 4 > 0$ 是同解不等式，其中 $m$ ， $n$ 是整数，试求 $m$ ， $n$ 的值．

查看试题解析