云南省昆明市西山区2022-2023学年七年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 年月日,昆明市第七届运动会首场新闻发布会在昆明市寻甸回族彝族自治县举行,组委会发布了本届运动会的吉祥物“牛小乐”,下面选项中的四张图片中,可以由图平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列事件中,最适合采用全面调查的是( )A、对市面上某种品牌食盐含碘量的调查 B、对全国中学生节水意识的调查 C、对一枚用于发射卫星的运载火箭零部件的调查 D、对某批次灯泡使用寿命的调查3. 在平面直角坐标系中,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,是直线外一点,是线段的中点,连接 , 过点作 , 垂足为点 , 则点到直线的距离是( )
2. 下列事件中,最适合采用全面调查的是( )A、对市面上某种品牌食盐含碘量的调查 B、对全国中学生节水意识的调查 C、对一枚用于发射卫星的运载火箭零部件的调查 D、对某批次灯泡使用寿命的调查3. 在平面直角坐标系中,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,是直线外一点,是线段的中点,连接 , 过点作 , 垂足为点 , 则点到直线的距离是( )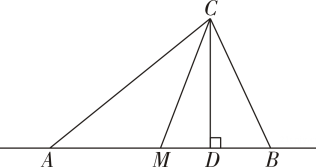 A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度5. 已知 , 是方程的解,那么的值为( )A、 B、 C、 D、6. 二元一次方程组的解是( )A、 B、 C、 D、7. 在实数: , , , , , , 两个之间依次增加一个中,无理数有( )A、个 B、个 C、个 D、个8. 已知 , 下列不等式的变形不正确的是( )A、 B、 C、 D、9. 平面直角坐标系中,将点向左平移个单位长度再向上平移个单位长度得到的点的坐标是( )A、 B、 C、 D、10. 在数轴上表示不等式组的解集表示正确的是( )A、
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度5. 已知 , 是方程的解,那么的值为( )A、 B、 C、 D、6. 二元一次方程组的解是( )A、 B、 C、 D、7. 在实数: , , , , , , 两个之间依次增加一个中,无理数有( )A、个 B、个 C、个 D、个8. 已知 , 下列不等式的变形不正确的是( )A、 B、 C、 D、9. 平面直角坐标系中,将点向左平移个单位长度再向上平移个单位长度得到的点的坐标是( )A、 B、 C、 D、10. 在数轴上表示不等式组的解集表示正确的是( )A、 B、
B、 C、
C、 D、
D、 11. 下列命题中:
11. 下列命题中:对顶角相等;在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行;如果两个实数的平方相等,那么这两个实数也相等;立方根等于它本身的实数只有或;二元一次方程的整数解只有组.
其中真命题有( )
A、个 B、个 C、个 D、个12. 如图,已知 , 为、之间的一点,连接、 , , , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共8.0分)
-
13. 如果把街巷记为 , 那么街巷可以表示为 .14. 某校八年级名学生参加生命安全知识测试,测试分数均大于或等于且小于 , 分数段的频率分布情况如表所示,结合表的信息,可得测试分数在分数段的学生有 名
分数段
频率
15. 若实数、满足等式: , 则 .16. 已知,在同一平面内, , , 的平分线交直线于点 , 那么度数为 .三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 在平面直角坐标系中, , , 三点的坐标分别为 , .
 (1)、画出 , 并将平移后,使点的对应点为点 , 点的对应点为点 , 点的对应点为点 , 画出平移后的 , 并直接写出点的坐标;(2)、求出的面积.19. 年全国青少年定向教育竞赛在气候宜人的云南昆明开赛本次比赛历时天,设百米定向、专线定向、短距离赛和短距离接力赛个项目共有个学校和单位的名中小学生参赛某中学为了解学生对个项目:百米定向,:专线定向,:短距离赛,:短距离接力赛的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查每个被调查的学生必须选择而且只能在这个项目中选择一项将数据进行整理并绘制成下面两幅不完整的统计图.
(1)、画出 , 并将平移后,使点的对应点为点 , 点的对应点为点 , 点的对应点为点 , 画出平移后的 , 并直接写出点的坐标;(2)、求出的面积.19. 年全国青少年定向教育竞赛在气候宜人的云南昆明开赛本次比赛历时天,设百米定向、专线定向、短距离赛和短距离接力赛个项目共有个学校和单位的名中小学生参赛某中学为了解学生对个项目:百米定向,:专线定向,:短距离赛,:短距离接力赛的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查每个被调查的学生必须选择而且只能在这个项目中选择一项将数据进行整理并绘制成下面两幅不完整的统计图. (1)、这次调查中,一共调查了 ▲ 名学生,扇形统计图中“”所在扇形的圆心角的度数为 ,并补全条形统计图:(2)、若全校有名学生,请估计喜欢专线定向的学生有多少名?20. 如图, , .
(1)、这次调查中,一共调查了 ▲ 名学生,扇形统计图中“”所在扇形的圆心角的度数为 ,并补全条形统计图:(2)、若全校有名学生,请估计喜欢专线定向的学生有多少名?20. 如图, , . (1)、求证:;(2)、若是的平分线, , 求的度数.21. 已知:和是的两个不同的平方根,是的立方根求、、的值.22. 月日,昆明市组织举办年“文化和自然遗产日”非遗宣传展示系列活动,在小渔村、福安村两个主会场开展了丰富多彩的非遗文化体验、展示活动年“文化和自然遗产日”非遗宣传展示活动的主题为“加强非遗系统性保护,促进可持续发展”昆明市围绕主题,采取市、县区联动的方式,通过在市级主会场和各县市区分会场举行余项非遗宣传展示系列活动,让非遗“飞入寻常百姓家”,营造出昆明非遗保护传承的良好氛围,充分展示昆明市非物质文化遗产保护传承的新成果、新亮点为满足游客的需求,主办方从非遗传承人处购进安宁扎染和宝峰贴花用于现场售卖:第一批购进份安宁扎染和份宝峰贴花,支付元;第二批购进份安宁扎染和份宝峰贴花,支付元;(1)、求安宁扎染和宝峰贴花的进价.(2)、根据前期的市场调查,主办方将安宁扎染定价为元份,宝峰贴花定价为元份,全部销售完毕后,能获得多少利润?23. 昆明城区年月日共出现以上高温天气天,为年以来昆明地区同期出现高温天气天数的第三多,其中日连续天最高气温 , 超过日最高气温为 , 创今年之最“炎炎夏日,酷暑难耐,寻一处清凉,得一份心静”西山区某家电超市决定采购甲、乙两种型号的电风扇进行销售,经市场调研得到信息如表所示:
(1)、求证:;(2)、若是的平分线, , 求的度数.21. 已知:和是的两个不同的平方根,是的立方根求、、的值.22. 月日,昆明市组织举办年“文化和自然遗产日”非遗宣传展示系列活动,在小渔村、福安村两个主会场开展了丰富多彩的非遗文化体验、展示活动年“文化和自然遗产日”非遗宣传展示活动的主题为“加强非遗系统性保护,促进可持续发展”昆明市围绕主题,采取市、县区联动的方式,通过在市级主会场和各县市区分会场举行余项非遗宣传展示系列活动,让非遗“飞入寻常百姓家”,营造出昆明非遗保护传承的良好氛围,充分展示昆明市非物质文化遗产保护传承的新成果、新亮点为满足游客的需求,主办方从非遗传承人处购进安宁扎染和宝峰贴花用于现场售卖:第一批购进份安宁扎染和份宝峰贴花,支付元;第二批购进份安宁扎染和份宝峰贴花,支付元;(1)、求安宁扎染和宝峰贴花的进价.(2)、根据前期的市场调查,主办方将安宁扎染定价为元份,宝峰贴花定价为元份,全部销售完毕后,能获得多少利润?23. 昆明城区年月日共出现以上高温天气天,为年以来昆明地区同期出现高温天气天数的第三多,其中日连续天最高气温 , 超过日最高气温为 , 创今年之最“炎炎夏日,酷暑难耐,寻一处清凉,得一份心静”西山区某家电超市决定采购甲、乙两种型号的电风扇进行销售,经市场调研得到信息如表所示:甲种型号电风扇
乙种型号电风扇
进价单位:元台
售价单位:元台
(1)、若超市准备用不超过元的资金采购这两种型号的电风扇共台,求甲种型号的电风扇最多能采购多少台?(2)、在条件下,若超市全部售完这台电风扇所获总利润不低于元,有哪几种进货方案?并通过计算说明哪种方案获得的总利润最大?最大利润是多少?24. 【数学史料】孙子算经是中国古代重要的数学著作之一,相传为春秋时期著名军事家孙武所作,孙子算经中记载的“同余思想”为我们研究周期性变化规律提供了研究方法.
【应用举例】
例如: , , , , , , , , 我们可以发现的指数幂个位数字是分别是 , , , 这四个数字不断重复出现,因此我们把它称为周期性变化规律,其周期为是第个指数幂,用序号 , 商余 , 于是第个指数幂个位数字与第一个指数幂相同;是第个指数幂,用序号 , 商余 , 于是第个指数幂个位数字与第二个指数幂相同;是第个指数幂,用序号 , 商余 , 于是第个指数幂个位数字与第三个指数幂相同;是第个指数幂,用序号 , 商余 , 于是第个指数幂个位数字与第四个指数幂相同 , 按照这样方法第个指数幂的个位数字,就用 , 余数是 , 所以的个位数字与第三个指数幂相同,都是也就是说用序号分别除以周期,所得余数相同的指数幂其个位数字相同.
【归纳小结】应对周期性变化规律,找准变化周期,用同余余数相同关系解决问题.
【拓广探索】已知是不为的实数,我们把称为的差倒数,如:的差倒数是现已知 , 是的差倒数,是的差倒数,是的差倒数,以此类推,是的差倒数为正整数 .
(1)、已知当时的差倒数为周期性变化规律,则的值为 ;(2)、计算;(3)、记 , 用含的式子表示的值.