云南省昆明市嵩明县2022-2023学年七年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 皮影戏是中国民间古老的传统艺术,年中国皮影戏人选人类非物质文化遗产代表作名录,平移如图所示的孙悟空皮影造型,能得到下列图中的( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列实数中,是正数的是( )A、 B、 C、 D、3. 下列选项中,与是对顶角的是( )A、
2. 下列实数中,是正数的是( )A、 B、 C、 D、3. 下列选项中,与是对顶角的是( )A、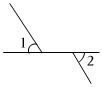 B、
B、 C、
C、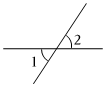 D、
D、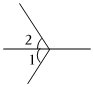 4. 下列调查中,最适合采用全面调查的是( )A、调查嵩明县中小学生的平均睡眠时间 B、调查一个班学生的体重 C、调查云南省空气质量情况 D、调查一批护眼灯的使用寿命5. 将不等式的解集表示在数轴上,正确的是( )A、
4. 下列调查中,最适合采用全面调查的是( )A、调查嵩明县中小学生的平均睡眠时间 B、调查一个班学生的体重 C、调查云南省空气质量情况 D、调查一批护眼灯的使用寿命5. 将不等式的解集表示在数轴上,正确的是( )A、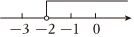 B、
B、 C、
C、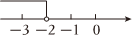 D、
D、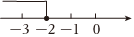 6. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 按一定规律排列的单项式: , , , , , , 则第个单项式是( )A、 B、 C、 D、8. 若 , 则的值是( )A、 B、 C、 D、9. 如图,关于小明家相对于学校的位置,下列描述最正确的是( )
6. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 按一定规律排列的单项式: , , , , , , 则第个单项式是( )A、 B、 C、 D、8. 若 , 则的值是( )A、 B、 C、 D、9. 如图,关于小明家相对于学校的位置,下列描述最正确的是( )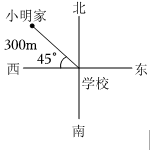 A、在距离学校米处 B、在学校的东南方向 C、在南偏东方向米处 D、在学校北偏西方向米处10. 已知 , 下列不等式成立的是( )A、 B、 C、 D、11. 数轴上点所表示的实数可能是( )
A、在距离学校米处 B、在学校的东南方向 C、在南偏东方向米处 D、在学校北偏西方向米处10. 已知 , 下列不等式成立的是( )A、 B、 C、 D、11. 数轴上点所表示的实数可能是( )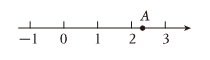 A、 B、 C、 D、12. “今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何”是《孙子算经》卷中著名数学问题.意思是:鸡兔同笼,从上面数,有35个头;从下面数,有94条腿.问鸡兔各有多少只?若设鸡有只,兔有只,则所列方程组正确的是( )A、 B、 C、 D、
A、 B、 C、 D、12. “今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何”是《孙子算经》卷中著名数学问题.意思是:鸡兔同笼,从上面数,有35个头;从下面数,有94条腿.问鸡兔各有多少只?若设鸡有只,兔有只,则所列方程组正确的是( )A、 B、 C、 D、二、填空题(本大题共4小题,共8.0分)
-
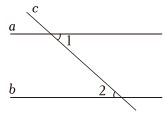
13. 1的算术平方根是 .14. 在平面直角坐标系中,已知点在轴上,则 .15. 如图, , 若 , 则
 16. 对于 , 定义一种新运算“”: , 等式右边是通常的加法和乘法运算如: , 那么 .
16. 对于 , 定义一种新运算“”: , 等式右边是通常的加法和乘法运算如: , 那么 .三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 解方程组:(1)、;(2)、 .19. 解不等式组: , 并写出它的所有整数解.20. 如图,的三个顶点坐标分别为 , , .
 (1)、将向右平移个单位,作出;(2)、直接写出 , , 三点的坐标.21. 某校开展“我是小中医传承大国粹”活动,其中有中医香囊制作,中药饮片辨识,中药炮制,药香制作,中草药识别五个兴趣小组,要求每名学生必选且只能选一项,现随机抽查了名学生,并将其结果绘制成如下不完整的条形图和扇形图.
(1)、将向右平移个单位,作出;(2)、直接写出 , , 三点的坐标.21. 某校开展“我是小中医传承大国粹”活动,其中有中医香囊制作,中药饮片辨识,中药炮制,药香制作,中草药识别五个兴趣小组,要求每名学生必选且只能选一项,现随机抽查了名学生,并将其结果绘制成如下不完整的条形图和扇形图.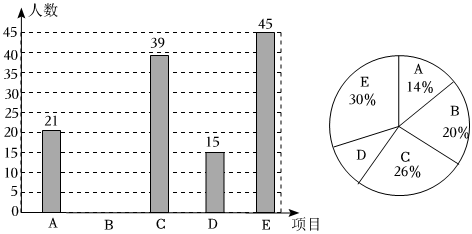
请结合以上信息解答下列问题:
(1)、m= ▲ , 并补全上面的条形统计图;(2)、已知该校共有名学生,请你估计该校最喜爱“中药饮片辨识”的有多少人.22. 填空完成推理过程:
如图, , 的平分线交于点 , 交的延长线于点 , , 求证: .
请将下面的证明过程补充完整:
证明:已知 ,
▲ .
平分 ,
▲ .
,
▲ .
23. 为迎接暑假旅游高峰的到来,某旅游纪念品商店决定购进 , 两种纪念品若购进种纪念品件,种纪念品件,需要元;若购进种纪念品件,种纪念品件,需要元.(1)、求购进 , 两种纪念品每件各需多少元?(2)、若该商店决定购进这两种纪念品共件考虑市场需求和资金周转,购买这件纪念品的资金不少于元,且不足元,那么该商店共有几种进货方案?24. 如图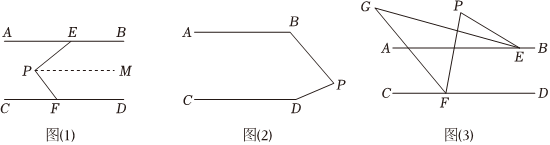
【问题探究】如图(1), , , , 求的度数小嵩想到了以下方法:解:如图(1),过点作 ,
两直线平行,内错角相等 .
已知 ,
平行于同一条直线的两直线平行 .
两直线平行,同旁内角互补 .
已知 ,
.
.
即 .
(1)、【问题迁移】如图(2), , , , 直接写出 ;(2)、【问题拓展】如图(3), , , , 的平分线和的平分线交于点 , 求的度数写出必要的推理过程 .