云南省玉溪市峨山县2022-2023学年七年级下学期期末数学试题
试卷更新日期：2023-09-19 类型：期末考试
一、选择题（本大题共12小题，每小题3分，共36分）
-
1. 下列四个实数中，最小的数是（ ）A、0 B、 C、－1 D、2. 下列说法中，正确的是（ ）A、相等的角是对顶角 B、两条直线被第三条直线所截，同位角相等 C、在同一平面内，过一点有且仅有一条直线垂直于已知直线 D、一个锐角的补角可能等于该锐角的余角3. 下列运算中，正确的是（ ）A、 B、 C、2a＋3b＝5ab D、－（a－b）＝b－a4. 如图，在象棋盘上建立直角坐标系，若“象”位于（2，0），则“炮”位于（ ）
A、（3，－2） B、（4，－2） C、（－2，4） D、（－2，3）5. 若代数式有意义，则x的取值范围是（ ）A、x≥0 B、x＞4 C、x≥4 D、x≤46. 如图，AB∥CD ， EG平分∠AEN ， 若∠EFD＝108°，则∠GEN的度数为（ ）
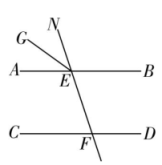A、36° B、54° C、72° D、108°7. 若方程mx＋y＝5的一个解是 ， 则m的值为（ ）A、－3 B、3 C、－2 D、28. 为了调查我市某校学生的视力情况，在全校的2000名学生中随机抽取了200名学生进行调查，下列说法正确的是（ ）A、此次调查属于全面调查 B、样本容量是200 C、2000名学生是总体 D、被抽取的每一名学生称为个体9. 不等式1－x＞x－1的解集是（ ）A、x＜1 B、x＞－1 C、x＞1 D、x≤－110. 如图是两个形状、大小完全一样的小长方形拼接而成的图形，已知AB＝5，CD＝3，则此图形的面积为（ ）
A、6 B、8 C、10 D、1211. 小明原有存款52元，小亮原有存款70元，从这个月开始，小明每月存15元零花钱，小亮每月存12元零花钱，设经过x个月后小明的存款超过小亮，可列不等式为（ ）A、52＋15x＞70＋12x B、52＋15x＜70＋12x C、52＋12x＞70＋15x D、52＋12x＜70＋15x12. 如图，用字母“C”、“H”按一定规律拼成图案，其中第1个图案中有4个H，第2个图案中有6个H，第3个图案中有8个H，……，按此规律排列下去，第2023个图案中字母H的个数为（ ）
A、4044 B、4046 C、6069 D、4048二、填空题（本大题共4小题，每小题2分，共8分）
-
13. 4的平方根是14. 如图，直线AB⊥CD于点O ， EF为过点O的直线，∠1＝50°，则∠2的度数为 ．
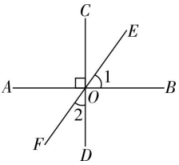15. 关于x的不等式组无解，则a的取值范围是 ．16. 某公园的门票价格为：成人票8元/张，儿童票3元/张，某旅游团买门票共花费44元，则该旅游团去公园游玩的人数是 ．三、解答题（本大题共8小题，共56分）
-
17. 计算： ．18. 解不等式组 ， 并把解集表示在数轴上．19. 已知点A（3a－9，2a－10），解答下列问题：(1)、若点B的坐标为（4，5），且AB∥y轴，求a的值；(2)、若点A在第四象限，且a是整数，求点A的坐标．20. 学校组织学生和教师共300人到市区进行研学活动，计划租用大巴车和中巴车10辆，已知每辆大巴车的座位数比每辆中巴车多20个，且租用5辆大巴车和5辆中巴车恰好全部坐满，求每辆大巴车和每辆中巴车的座位数．（列二元一次方程组解答）21. 每年的4月23日是世界读书日，读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然正气．某校开展了“共享阅读、向上人生”的读书活动，活动中，为了解学生对书籍种类（A：艺术类；B：科技类；C：文学类；D：体育类）的喜欢情况，在全校范围内随机抽取若干名学生，进行问卷调查（每个被调查的学生必须选择且只能选择四类中的一类），将数据进行整理并绘制成下列两幅不完整的统计图．
根据统计图表提供的信息，解答下列问题：
(1)、这次调查中，一共调查了名学生；(2)、补全条形统计图，并求出扇形统计图中“D”所在扇形的圆心角度数；(3)、若全校有2000名学生，请估计喜欢科技类书籍的学生人生有多少名？22. 如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H ， ∠C＝∠EFG ， ∠CED＝∠GHD ．
(1)、求证：AB∥CD；(2)、若∠EHF＝90°，∠D＝30°，求∠AEM的度数．23. 如图，在平面直角坐标系中，点A、B的坐标分别为（－2，0）、（4，0），现在把线段AB向上平移2个单位长度，再向右平移2个单位长度，得到线段CD ， 连接AC、BD ．
(1)、请直接写出点C、点D的坐标；(2)、在x轴上是否存在一点P ， 使得△CDP的面积是△BDP面积的2倍？若存在，求出点P的坐标；若不存在，请说明理由．24. 围绕“建设国家级现代农业产业示范园区”总体目标，云南某县引进多种口感好的橙子品种，助推乡村振兴．某超市看好甲、乙两种橙子的市场价值，经调查甲种橙子进价每千克a元，售价每千克16元；乙种橙子进价每千克b元，售价每千克24元．(1)、该超市购进甲种橙子15千克和乙种橙子20千克需要430元；购进甲种橙子10千克和乙种橙子8千克需要212元，求a、b的值；(2)、超市决定每天购进甲、乙两种橙子共100千克（两种橙子的数量都是整数），且投入资金不少于1160元又不超过1168元，该超市有哪几种购买方案？哪种方案获得的利润最大，最大利润是多少元？