云南省曲靖市2022-2023学年七年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 9的平方根是( )A、 B、 C、 D、2. 在平面直角坐标系中到轴的距离是( )A、 B、 C、 D、3. 某校七年级有名学生,随机抽取名学生进行视力调查,下列说法错误的是( )A、样本容量是 B、样本是抽取的名学生的视力
C、总体是该校名学生的视力 D、个体是每个学生4. 已知、满足方程组 , 则的值为( )A、1 B、2 C、3 D、45. 实数的值在( )A、和之间 B、和之间 C、和之间 D、和之间6. 在 , , , , , , 每两个之间的个数逐渐增加个这个数中,无理数有( )A、个 B、个 C、个 D、个7. 在下列各式中,计算正确的是( )A、 B、
C、 D、8. 如图,沿所在直线向右平移到 , 连接 , 已知 , , 则的长为( )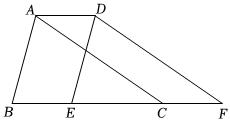 A、 B、 C、 D、9. 如图, , , , 则下列说法正确的是( )
A、 B、 C、 D、9. 如图, , , , 则下列说法正确的是( ) A、
A、
B、
C、
D、10. 已知关于的不等式的解集为 , 则的取值范围是( )A、 B、 C、 D、11. 如图, , , , 若 , 则的度数为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,正方形 , 正方形 , 正方形按如图所示的顺序排列,其中 , , 在同一条直线上,则点的坐标为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,正方形 , 正方形 , 正方形按如图所示的顺序排列,其中 , , 在同一条直线上,则点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共8.0分)
-
13. 如图,若 , , 则的度数为 .
 14. 某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后,列频数分部表部分如下:
14. 某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后,列频数分部表部分如下:项目
乒乓球
羽毛球
篮球
足球
频数
百分比
则的值为 .
15. 从甲地到乙地有一段上坡路与一段平路,如果上坡每小时走 , 平路每小时走 , 下坡每小时走 , 那么从甲地到乙地需要分钟,从乙地到甲地需要分钟,甲地到乙地全程是多少?根据题意,老师给出的方程组为 , 则方程组中表示 .16. 若整数使得关于的不等式组有且仅有个整数解,则所有满足条件的整数的值之和为 .三、计算题(本大题共1小题,共6.0分)
-
17. 在等式中,当时,;当时, , 当时, , 求这个等式中、、的值.
四、解答题(本大题共7小题,共50.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 计算:19. 解不等式组 , 并将其解集在数轴上表示出来.20. 学校食堂为了了解某种点心的甜度是否适中,食堂管理人员将这种点心随机免费送给名学生品尝,调查结果如下:
A、太甜
B、稍甜
C、适中
D、稍淡A、、、、、、、、、
C、、、、、、、、、(1)、学习了统计的小明同学根据上面调查结果画出如下不完整条形统计图,请补全条形统计图;
(2)、根据调查结果,估计该校名学生对这种点心认为甜度适中的有多少人? 21. 如图, , 相交于点 , 平分 .
21. 如图, , 相交于点 , 平分 . (1)、若 , 求的度数;
(1)、若 , 求的度数;
(2)、若:: , , 且 , 求证 .22. 2022年月日至日冬季奥运会在北京举行,某商店计划同时购进“冰墩墩”和“雪容融”两种玩具,据了解,只“冰墩墩”和只“雪容融”的进价共计元,只“冰墩墩”和只“雪容融”的进价共计元.
(1)、求“冰墩墩”和“雪容融”两种玩具每只进价分别是多少元;
(2)、该商店计划将“冰墩墩”售价定为元个,“雪容融”售价定为元个,若该商店总共购进“冰墩墩”和“雪容融”个进行销售,且全部售完,要至少盈利元,求购进的“冰墩墩”不能少于多少个?
-

