云南省昆明市盘龙区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-09-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共12个小题，每小题只有一个正确选项，每小题3分，共36分）

1. $\sqrt{4}$ 的值是（）

A、2 B、 $- 2$ C、 $\pm 2$ D、4

查看试题解析
2. 为了解某地区2023年七年级20000名学生的身高情况，从中随机抽取了500名学生的身高情况进行统计分析．下列说法中，正确的是（）

A、每名学生是个体 B、20000名学生是总体 C、500名学生是抽取的一个样本 D、抽取的样本容量为500

查看试题解析
3. 若 $a > b$ ，则下列不等式中，不成立的是（）

A、 $a - 1 > b - 1$ B、 $- 3 a < - 3 b$ C、 $3 a > 3 b$ D、 $\frac{a}{5} < \frac{b}{5}$

查看试题解析
4. 下列命题：①相等的角是对顶角；②邻补角是互补的角；③两条直线被第三条直线所截，同位角相等；④在同一平面内，过一点有且只有一条直线与已知直线垂直．
其中真命题的个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 某车间有120名工人生产一种如图所示的无盖正方体包装箱，已知1名工人每天可以生产200块侧面或150块底面（底面和侧面材料不同），4块侧面和1块底面正好可以做成一个无盖包装箱，应如何分配工人生产侧面或底面，才能使生产的侧面和底面正好配套?若设安排 $x$ 名工人生产侧面， $y$ 名工人生产底面，则下列方程组正确的是（）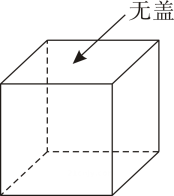

A、 ${\begin{array}{l} x + y = 120 \\ 200 x = 150 y \end{array}$ B、 ${\begin{array}{l} x + y = 120 \\ 4 \times 200 x = 150 y \end{array}$ C、 ${\begin{array}{l} x + y = 120 \\ 200 x = 4 \times 150 y \end{array}$ D、 ${\begin{array}{l} x + y = 100 \\ 200 x = 2 \times 150 y \end{array}$

查看试题解析
6. 如图，是某学校的示意图，若综合楼的位置在点 $(- 2 ， 0)$ ，食堂的位置在点 $(1 ， 3)$ ，则教学楼的位置在点（）

A、 $(- 4 ， 2)$ B、 $(- 5 ， 2)$ C、 $(0 ， - 4)$ D、 $(- 4 ， 0)$

查看试题解析
7. 某校为了解七年级700名学生上学期参加社会实践活动的时间，随机对该年级部分学生进行了调查．根据收集的数据绘制了下面的频数分布直方图，则以下说法正确的是（）

A、一共调查了40名学生 B、该频数分布直方图的组距为2 C、该频数分布直方图的组数为2 D、随机抽取的学生中参加社会实践活动时间不少于 $10 h$ 的有32名的学生

查看试题解析
8. 某商店为了促销一种定价为3元的商品，采取下列方式优惠销售：若一次性购买不超过5件，按原价付款；若一次性购买5件以上，超过部分按原价的八折付款．如果小明有30元钱，那么他最多可以购买该商品（）

A、9件 B、10件 C、11件 D、12件

查看试题解析
9. 若方程组 ${\begin{array}{l} 3 x + y = k + 1 \\ x + 3 y = 3 \end{array}$ 的解x，y满足 $0 < x + y < 1$ ，则k的取值范围是（）

A、 $- 1 < k < 0$ B、 $- 4 < k < 0$ C、 $0 < k < 8$ D、 $k > - 4$

查看试题解析
10. 在数学拓展课《折叠的奥秘》中，老师提出一个问题：如图，有一条宽度相等的长方形纸带，将纸条沿 $A B$ 折叠一下，若 $∠ 1 = 130 °$ ，则 $∠ 2$ 的度数为（）

A、 $115 °$ B、 $120 °$ C、 $130 °$ D、 $110 °$

查看试题解析
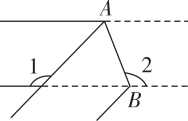11. 甲、乙两人在解方程组 ${\begin{array}{l} a x + 5 y = 15 ① \\ 4 x = b y - 2 ② \end{array}$ 时，甲看错了方程①中的 $a$ ，解得 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，乙看错了方程②中的 $b$ ，解得 ${\begin{array}{l} x = 5 \\ y = 4 \end{array}$ ，则 $a^{2023} - {(- \frac{b}{10})}^{2022}$ 的值为（）

A、2 B、 $- 2$ C、0 D、 $- 3$

查看试题解析
12. 定义运算 $a \otimes b = a^{2} - 2 a b$ ，下面给出了关于这种运算的几个结论：
① $2 \otimes 5 = - 16$ ；② $\sqrt[3]{2 \otimes (- 1)}$ 是无理数；③方程 $x \otimes y = 0$ 不是二元一次方程；其中正确的是（）

A、①② B、②③ C、③ D、①③

查看试题解析

二、填空题（本大题共4小题，每小题2分，共8分）

13. 若 $x^{2} = 25$ ，则x= ．

查看试题解析
14. 如图，直线 $A B$ 、 $C D$ 、 $E F$ 交于点 $O ， ∠ A O C ： ∠ C O E = 1 ： 2$ ，若 $∠ B O D = 28 °$ ，则 $∠ B O E =$ °．

查看试题解析
15. 如果不等式组 ${\begin{array}{l} 3 x < 2 x + 2 \\ x < m \end{array}$ 的解集是 $x < 2$ ，那么 $m$ 的取值范围是．

查看试题解析
16. 如图，第一象限内有两点 $P (m - 3 ， n) ， Q (m ， n - 2)$ ，将线段 $P Q$ 平移使点 $P$ 、 $Q$ 分别落在两条坐标轴上，则点 $P$ 平移后的对应点的坐标是．

查看试题解析

三、解答题（本大题共8个题，共56分.解答时必须写出必要的计算过程、推理步骤或文字说明.）

17. 计算： $\sqrt{(- 2)^{2}} - \sqrt[3]{125} + | \sqrt{3} - 2 | + \sqrt{3}$ .

查看试题解析
18. 解方程组： ${\begin{array}{l} x + y = 4 \\ 5 x - y = 2 \end{array}$ .

查看试题解析
19. 解不等式组 ${\begin{array}{l} 2 x + 1 \geq - 1 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$ ，并把解集表示在数轴上．

查看试题解析
20. 如图，三角形 $A B C$ 的三个顶点的坐标分别为： $A (- 1 ， 4) ， B (- 4 ， - 1)$ ， $C (1 ， 1)$ ．若将三角形 $A B C$ 向右平移4个单位长度，再向下平移3个单位长度得到三角形 $A^{'} B^{'} C^{'}$ ，且点 $A ， B ， C$ 的对应点分别是 $A^{'} ， B^{'} ， C^{'}$ ．

(1)、画出平移后的三角形 $A^{'} B^{'} C^{'}$ ，并直接写出点 $C'$ 的坐标；

(2)、若三角形 $A B C$ 内有一点 $P (a ， b)$ 经过上述平移后的对应点为 $P^{'}$ ，则点 $P^{'}$ 的坐标；

(3)、请直接写出三角形 $A B C$ 的面积．

查看试题解析
21. 2023年5月30日神舟十六号发射成功，载荷专家桂海潮是飞天的宇航员之一．近期，昆明市某校学生参加了“筑梦航空”知识竞赛，为了解全校学生竞赛成绩的情况，随机抽取了部分学生的成绩进行统计，分成 $A$ 、 $B$ 、 $C$ 、 $D$ 四个等级，并绘制出如下两幅不完整的统计图．

请根据以上信息，解答下列问题：

(1)、本次被抽取的学生共有 ▲ 名，并补全条形统计图；

(2)、 $D$ 等级所在扇形的圆心角度数为°；

(3)、若该校共有2400名学生，估计全校成绩在 $C$ 等级的学生有多少名?

查看试题解析
22. 如图，在三角形 $A B C$ 中，点 $D ， E$ 在 $A B$ 边上，点 $F$ 在 $A C$ 边上，连接 $E F$ ， $E F / / D C$ ，点 $H$ 在 $B C$ 边上，连接 $D H$ ，且 $∠ 1 + ∠ 2 = 180 °$ ．

(1)、求证： $∠ A = ∠ B D H$ ；

(2)、若 $C D$ 平分 $∠ A C B ， ∠ A F E = 30 °$ ，求 $∠ B H D$ 的度数．

查看试题解析
23. 为保持空气质量的良好率，降低空气污染，昆明某公交公司决定更换节能环保的新能源公交车，计划购买 $A$ 型和 $B$ 型两种新能源公交车，其中每台的价格，年载客量如下表：

          $A$ 型
          $B$ 型
价格（万元/台）
          $a$
          $b$
年载客量（万人/年）
60
100
若购买 $A$ 型公交车1辆， $B$ 型公交车2辆，共需400万元；若购买 $A$ 型公交车2辆， $B$ 型公交车1辆，共需350万元．

(1)、求 $a ， b$ 的值；

(2)、现准备计划购买 $A$ 型和 $B$ 型两种新能源公交车共10辆，如果该公司购买 $A$ 型和 $B$ 型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次．请你设计一个方案，使得购车总费用最少．

查看试题解析
24. 酷热的夏天之后汛期即将来临，防汛指挥部在盘龙江两岸各安置了探照灯，便于夜间查看江水及两岸河堤的情况．如图一，灯 $A$ 射线自 $A M$ 顺时针旋转至 $A N$ 便立即回转，灯 $B$ 射线自 $B P$ 顺时针旋转至 $B Q$ 便立即回转，两灯不停交叉照射巡视．若灯 $A$ 转动的速度是 $a ° /$ 秒，灯 $B$ 转动的速度是 $b ° /$ 秒，且 $a$ 、 $b$ 满足 $| a - 3 | + (b - 1)^{2} = 0$ ．
假定这一带盘龙江两岸河堤是平行的，即 $P Q / / M N$ ，且 $∠ B A N = 45 °$ ．

(1)、 $a =$ ， $b =$ ；

(2)、若灯 $B$ 射线先转动30秒，灯 $A$ 射线才开始转动，在灯 $B$ 射线到达 $B Q$ 之前， $A$ 灯转动秒时，两灯的光束第一次互相平行；

(3)、如图2，两灯同时转动秒，在灯 $A$ 射线到达 $A N$ 之前，若射出的光束 $A C ， B C$ 交于点 $C$ ．
① $∠ B C A =$ ▲ （用含的代数式表示）；

②过 $C$ 作 $C D ⊥ A C$ 交 $P Q$ 于点 $D$ ，则在转动过程中，猜想： $∠ B A C$ 与 $∠ B C D$ 有怎样的数量关系，并说明理由．

查看试题解析

	$A$ 型	$B$ 型
价格（万元/台）	$a$	$b$
年载客量（万人/年）	60	100