云南省昆明市盘龙区2022-2023学年八年级下学期期末数学试卷

试卷更新日期：2023-09-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{3}$ B、 $\sqrt{2.5}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{8}$

查看试题解析
2. 下列计算中正确的是（）

A、 $\sqrt{2} \times \sqrt{3} = 6$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{18} \div \sqrt{2} = 3$ D、 $2 \sqrt{2} - \sqrt{2} = 2$

查看试题解析
3. 如图，四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ，下列条件不能判定这个四边形是平行四边形的是（）

A、 $A B = D C$ ， $A D = B C$ B、 $∠ D A B = ∠ D C B$ ， $∠ A B C = ∠ A D C$ C、 $A O = C O$ ， $B O = D O$ D、 $A B / / C D$ ， $A D = B C$

查看试题解析
4. 若二次根式 $\sqrt{x + 1}$ 有意义，则 $x$ 的取值范围在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
5. 如图，直线 $y = a x + b (a \neq 0)$ 与x轴交点的横坐标为1，则关于x的方程 $a x + b = 0$ 的解为（）.

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
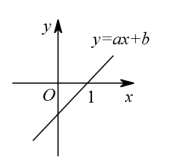6. 某校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班平均得分（　　）

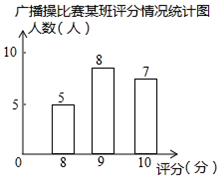A、9 B、6.67 C、9.1 D、6.74

查看试题解析
7. 图1是第七届国际数学教育大会（ICME）会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图 $2$ 所示的四边形 $O A B C$ ．若 $A B = B C = 2$ ，且 $∠ A O B = 30 °$ ，则 $O C$ 的长度为（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、4 D、 $2 \sqrt{5}$

查看试题解析
8. 观察分析下列数据： $0$ ， $- \sqrt{2} ， 2 ， - \sqrt{6} ， 2 \sqrt{2} ， - \sqrt{10} ， 2 \sqrt{3} ， ⋯$ ，根据数据排列的规律得到的第 $10$ 个数据的值是（）

A、 $3 \sqrt{2}$ B、 $- 3 \sqrt{2}$ C、 $2 \sqrt{5}$ D、 $- 2 \sqrt{5}$

查看试题解析
9. 对于一次函数 $y = - 2 x + 1$ 的相关性质，下列描述错误的是（）

A、函数图象经过第一、二、四象限 B、图象与y轴的交点坐标为 $(1 ， 0)$ C、y随x的增大而减小 D、图象与坐标轴调成三角形的面积为 $\frac{1}{4}$

查看试题解析
10. 如图，在 $∠ M O N$ 的两边上分别截取OA、OB，使 $O A = O B$ ；分别以点 $A 、 B$ 为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC若 $A B = 2 c m$ ，四边形 $O A C B$ 的面积为 $4 c m^{2}$ ．则OC的长为（）

A、 $2 c m$ B、 $3 c m$ C、 $4 c m$ D、 $5 c m$

查看试题解析
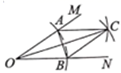11. 在物理实验课上，小宋利用滑轮组及相关器材进行实验，他把得到的拉力 $F (N)$ 和所悬挂物体的重力 $G (N)$ 的几组数据用电脑绘制成如图所示的图象 $($ 不计绳重和摩擦 $)$ ，请你根据图象判断以下结论不正确的是（）

A、施加的拉力 $F$ 随着物体重力 $G$ 的增加而增大 B、当拉力 $F = 2.7 N$ 时，物体的重力 $G = 3.5 N$ C、当物体的重力 $G = 7 N$ 时，拉力 $F = 4.5 N$ D、当滑轮组未悬挂物体在空中静止时，所用拉力为 $1 N$

查看试题解析
12. 如图所示，在 $△ P B C$ 中，分别取 $P B$ 、 $P C$ 的中点 $E$ 、 $F$ ，连接 $E F$ ，过点 $P$ 作 $P Q ⊥ E F$ ，垂足为 $Q$ ，将 $△ P B C$ 分割后拼接成矩形 $A B C D .$ 若 $E F = 4$ ， $P Q = 3$ ，则矩形 $A B C D$ 的面积是（）

A、 $6$ B、 $8$ C、 $12$ D、 $24$

查看试题解析

二、填空题（本大题共4小题，共8.0分）

13. $△ A B C$ 的三边长分别为 $1$ ， $\sqrt{3}$ ， $2$ ，那么 $△ A B C$ $($ 填“是”或“不是” $)$ 直角三角形．

查看试题解析

14. 如表记录了甲、乙、丙三名学生这学期的射击成绩的平均数和方差：

	甲	乙	丙
平均数	9.23	9.3	9.3
方差	0.23	0.017	0.057

根据表中的数据，要选择一名成绩好且发挥稳定的学生参加比赛，应选择．

查看试题解析

15. 将正比例函数 $y = - 5 x$ 向下平移 $3$ 个单位长度，得到一次函数 $y = a x + b$ ，则 $a b =$ ．

查看试题解析
16. 如图，四边形 $A B C D$ 是正方形，点 $E$ 在 $B C$ 边上，点 $F$ 在 $C D$ 的延长线上，满足 $B E = D F$ ，连接 $E F$ 与对角线 $B D$ 交于点 $G$ ，连接 $A F$ ， $A G$ ，若 $A F = \sqrt{10}$ ，则 $A G$ 的长为．

查看试题解析

三、解答题（本大题共8小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）

17. 计算：

(1)、 $\sqrt{27} \div \sqrt{3} + \sqrt{12} \times \sqrt{\frac{1}{3}} - \sqrt{5}$ ；

(2)、 $(\sqrt{5} + 2) (\sqrt{5} - 2) + {(2 \sqrt{3} + 1)}^{2}$ ．

查看试题解析
18. 已知：如图，四边形 $A B C D$ 是平行四边形， $A E / / C F$ ，且分别交对角线 $B D$ 于点 $E$ ， $F .$ 求证： $A E = C F$ ．

查看试题解析

19. 【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．

【实践发现】同学们随机收集芒果树、荔枝树的树叶各 $10$ 片，通过测量得到这些树叶的长 $y ($ 单位： $c m)$ ，宽 $x ($ 单位： $c m)$ 的数据后，分别计算长宽比，整理数据如下：

	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$
芒果树叶的长宽比	$3.8$	$3.7$	$3.5$	$3.4$	$3.8$	$4.0$	$3.6$	$4.0$	$3.6$	$4.0$
荔枝树叶的长宽比	$2.0$	$2.0$	$2.0$	$2.4$	$1.8$	$1.9$	$1.8$	$2.0$	$1.3$	$1.9$

【实践探究】分析数据如下：

	平均数	中位数	众数	方差
芒果树叶的长宽比	$3.74$	$b$	$4$	$0.0424$
荔枝树叶的长宽比	$a$	$1.95$	$c$	$0.0669$

【问题解决】

(1)、a= ，

b =

，

c =

；

(2)、A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大

.

”

$B$ 同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍 $.$ ”以上两位同学的说法中，合理的是同学；

(3)、现有一片长

11 c m

，宽

5.6 c m

的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．

查看试题解析

20. 在平面直角坐标系 $x O y$ 中，直线 $l_{1} ： y = 3 x$ 与直线 $l_{2} ： y = k x + b$ 交于点 $A (a ， 3)$ ，点 $B (2 ， 4)$ 在直线 $l_{2}$ 上．

(1)、求 $a$ 的值；

(2)、求直线 $l_{2}$ 的解析式；

(3)、直接写出关于 $x$ 的不等式 $3 x < k x + b$ 的解集．

查看试题解析
21. “中国人的饭碗必须牢牢掌握在咱们自己手中” $.$ 为扩大粮食生产规模，某粮食生产基地计划投入一笔资金购进甲、乙两种农机具，已知购进 $2$ 件甲种农机具和 $1$ 件乙种农机具共需 $3.5$ 万元，购进 $1$ 件甲种农机具和 $3$ 件乙种农机具共需 $3$ 万元．

(1)、求购进 $1$ 件甲种农机具和 $1$ 件乙种农机具各需多少万元？

(2)、若该粮食生产基地计划购进甲、乙两种农机具共 $10$ 件，且投入资金不少于 $9.8$ 万元又不超过 $12$ 万元，设购进甲种农机具 $m$ 件，则有哪几种购买方案？哪种购买方案需要的资金最少，最少资金是多少？

查看试题解析
22. 如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF＝BE，连接DF．

(1)、求证：四边形ADFE是矩形；

(2)、连接OF，若AD＝6，EC＝4，∠ABF＝60°，求OF的长度．

查看试题解析
23. 阅读下面的情景对话，然后解答问题：
老师：我们新定义一种三角形，两边平方和等于第三边平方的 $2$ 倍的三角形叫做奇异三角形．
小华：等边三角形一定是奇异三角形 $!$ 并做了如下证明：
设等边三角形的边长为 $a$ ，
$∵ a^{2} + a^{2} = 2 a^{2}$ ，
$∴$ 等边三角形一定是奇异三角形．
小明：那直角三角形是否存在奇异三角形呢？

(1)、在 $R t △ A B C$ 中，两直角边长分别是 $a = 5 \sqrt{2}$ 、 $b = 10$ ，这个三角形是否是奇异三角形？请说明理由．

(2)、在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = c$ ， $A C = b$ ， $B C = a$ ，且 $b > a$ ，若 $R t △ A B C$ 是奇异三角形，求 $a$ ： $b$ ： $c$ 的值．

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = 2 x + 4$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，过点 $B$ 的直线交 $x$ 轴正半轴于点 $C$ ，且 $△ A B C$ 面积为 $10$ ．

(1)、求点 $C$ 的坐标及直线 $B C$ 的解析式；

(2)、如图 $1$ ，设点 $F$ 为线段 $A B$ 中点，点 $G$ 为 $y$ 轴上一动点，连接 $F G$ ，以 $F G$ 为边向 $F G$ 右侧作正方形 $F G Q P$ ，在 $G$ 点的运动过程中，当顶点 $Q$ 落在直线 $B C$ 上时，求点 $G$ 的坐标．

查看试题解析