云南省昆明市官渡区2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 函数的图象过点( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 图书馆对上月借阅中外数学类书籍的情况进行了调查,统计数据如下表:
书名
几何原本
九章算术
数学家的眼光
怎样解题
借阅量人次
依据统计数据,为了更好地满足读者需求,该图书馆决定多购进上表四种书中的一种,你认为最可能多购进的是( )
A、几何原本 B、九章算术 C、数学家的眼光 D、怎样解题5. 原命题“平行四边形的两组对角分别相等”和它的逆命题“两组对角分别相等的四边形是平行四边形”,下列说法正确的是( )A、原命题和逆命题都正确 B、原命题和逆命题都错误 C、原命题错误,逆命题正确 D、原命题正确,逆命题错误6. 如图,要使▱为矩形,则可添加的条件是( ) A、 B、 C、 D、7. 如图,在△ABC中,AB=12,BC=13,AC=5,则BC边上的高AD为( )
A、 B、 C、 D、7. 如图,在△ABC中,AB=12,BC=13,AC=5,则BC边上的高AD为( )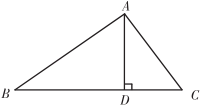 A、3 B、4 C、 D、4.88. 如图,在中, , , , 分别以点和点为圆心,大于的长为半径作弧,两弧相交于 , 两点,连接交于点 , 连接 , 到的长为( )
A、3 B、4 C、 D、4.88. 如图,在中, , , , 分别以点和点为圆心,大于的长为半径作弧,两弧相交于 , 两点,连接交于点 , 连接 , 到的长为( ) A、 B、 C、 D、9. 如图,在▱中, , 为上一点, , 分别为 , 的中点,则的长为( )
A、 B、 C、 D、9. 如图,在▱中, , 为上一点, , 分别为 , 的中点,则的长为( ) A、 B、 C、 D、不确定10. 如图,一次函数与的图象相交于点 , 则关于 , 的二元一次方程组的解是( )
A、 B、 C、 D、不确定10. 如图,一次函数与的图象相交于点 , 则关于 , 的二元一次方程组的解是( ) A、 B、 C、 D、11. 明朝数学家程大位在他的著作算法统宗中写了一首计算秋千绳索长度的词西江月:“平地秋千未起,踏板一尺离地送行二步恰竿齐,五尺板高离地”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺尺 , 将它往前推进两步尺,两步尺 , 此时踏板升高离地五尺尺 , 若绳索始终拉直,则秋千绳索的长是( )
A、 B、 C、 D、11. 明朝数学家程大位在他的著作算法统宗中写了一首计算秋千绳索长度的词西江月:“平地秋千未起,踏板一尺离地送行二步恰竿齐,五尺板高离地”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺尺 , 将它往前推进两步尺,两步尺 , 此时踏板升高离地五尺尺 , 若绳索始终拉直,则秋千绳索的长是( )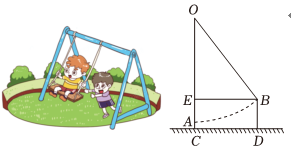 A、尺 B、尺 C、尺 D、尺12. 小渡同学匀速地向一个容器内注水,直至注满容器在注水的过程中,通过观察,小渡画出水面高度随时间变化的草图,如图,则这个容器的形状可能是( )
A、尺 B、尺 C、尺 D、尺12. 小渡同学匀速地向一个容器内注水,直至注满容器在注水的过程中,通过观察,小渡画出水面高度随时间变化的草图,如图,则这个容器的形状可能是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(本大题共4小题,共8.0分)
-
13. 二次根式中的取值范围是 .14. 走路不仅可以帮助减肥,还可以增强心肺功能、血管弹性、肌肉力量等小云、小南两名同学将同一星期内日步数的数据绘制成折线统计图,将步数方差分别记为 , , 从折线统计图可知, 填“”,“”或“=” .
 15. 在平面直角坐标系中,平行四边形的顶点、、则顶点的坐标是 .
15. 在平面直角坐标系中,平行四边形的顶点、、则顶点的坐标是 . 16. 如图,正方形的对角线、相交于点 , 是上的一点,连接 , 过点作 , 交于点 , 若四边形的面积是 , 则的长为 .
16. 如图,正方形的对角线、相交于点 , 是上的一点,连接 , 过点作 , 交于点 , 若四边形的面积是 , 则的长为 .
三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
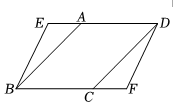
17. 计算:(1)、;(2)、 .18. 如图,在平行四边形中,点、分别在、延长线上,且求证:四边形为平行四边形.
 19. “双碳”背景下,新能源汽车在主流的大众消费群体中越来越受欢迎在会展中心举行一场新能源汽车车展活动中,共有三十几种不同品牌的新能源汽车参展,根据不同续航程将这些车分成六组,统计结果如下:
19. “双碳”背景下,新能源汽车在主流的大众消费群体中越来越受欢迎在会展中心举行一场新能源汽车车展活动中,共有三十几种不同品牌的新能源汽车参展,根据不同续航程将这些车分成六组,统计结果如下:分组
单位:公里
数量单位:辆
(1)、在参展的新能源汽车中,续航里程在 组的车最多;续航里程的中位数落在 组;(2)、小渡家看中了售价一样的甲、乙两款汽车,根据汽车鉴定机构发布的数据对这两款车的续航里程、百公里加速、智能化水平三项性能进行了打分百分制 , 如下表:续航里程分
百公里加速分
智能化水平分
甲车
乙车
小渡将续航里程、百公里加速、智能化水平三项性能的得分按::的比例确定甲、乙两款汽车的最终得分,并以此为依据做出了选择,你知道小渡的选择是什么吗?请写出计算过程进行说明.
20. 如图 , 在正方形网格中,每个小正方形的边长均为 , 的三个顶点都在格点上请判断的形状,并说明理由.
甲、乙两位同学运用所学知识,都说明了是直角三角形请你根据甲、乙两位同学的思路,补全解答过程.
甲同学说:“学习了勾股定理 , 已知三角形的三边,可根据勾股定理逆定理判断三角形的形状”
解:是直角三角形,理由如下:
在网格中由勾股定理可以算出: , , ,
▲ , ▲ ,
▲ .
▲ .
是角三角形.
乙同学说:“我可以运用全等三角形的相关知识,说明是直角三角形”
解:是直角三角形,理由如下:
如图 , 由网格可知: , , ,
在和中,
≌
▲ .
又在中, ,
▲ ,
,
是直角三角形.
21. 已知一次函数的图象经过点 , . (1)、结合函数图象,直接写出的解集;(2)、求一次函数的解析式;(3)、求面积.22. 2023年月日,云南人桂海潮乘坐神舟号飞船,成功遨游太空,圆了“飞天”梦想云官中学为了给学生们搭建一个航天梦,计划购买火箭模型和空间站模型共个两种模型均需购买 , 要求购买火箭模型的个数不多于空间站模型个数的倍通过市场调研,已知火箭模型每个元,空间站模型每个元设购买火箭模型个,购买总费用为元.(1)、求与的函数关系式,并直接写出自变量的取值范围;(2)、请你用函数的相关知识说明如何采购能使总费用最低?并求出最低费用.23. 【学习材料】
(1)、结合函数图象,直接写出的解集;(2)、求一次函数的解析式;(3)、求面积.22. 2023年月日,云南人桂海潮乘坐神舟号飞船,成功遨游太空,圆了“飞天”梦想云官中学为了给学生们搭建一个航天梦,计划购买火箭模型和空间站模型共个两种模型均需购买 , 要求购买火箭模型的个数不多于空间站模型个数的倍通过市场调研,已知火箭模型每个元,空间站模型每个元设购买火箭模型个,购买总费用为元.(1)、求与的函数关系式,并直接写出自变量的取值范围;(2)、请你用函数的相关知识说明如何采购能使总费用最低?并求出最低费用.23. 【学习材料】求直线向右平移个单位长度后的解析式.
第一步,在直线上任意取两点和;
第二步,将点和向右平移个单位长度得到点和 , 则直线就是直线向右平移个单位长度后得到的直线;
第三步,设直线的解析式为: , 将和代入得到:解得 , 所以直线的解析式为: .
(1)、【类比思考】若将直线向左平移个单位长度,则平移后的直线解析式为 ;
若先将直线向右平移个单位长度,再向下平移个单位长度,得到直线 , 则直线的解析式为 .
(2)、【拓展应用】已知一次函数的图象与直线关于轴对称,求一次函数的解析式;
若一次函数的图象绕点逆时针旋转后得到直线 , 则直线的解析式为 ▲ .
24. 如图
如图 , , , 平分 .
(1)、求证:四边形是菱形;(2)、如图 , , , 交于点 , 已知点是上一动点,连接 , 求周长的最小值.