云南省迪庆州2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 为研究实验田青稞产量的情况,科研人员得到甲、乙、丙、丁四块试验田产量的方差分别为 , , , , 哪一块试验田产量最稳定( )A、甲 B、乙 C、丙 D、丁3. 下列各组数中不能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 如图,在中, , 点、、分别是、、的中点,若 , 则的长为( )
 A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在 中,BE平分∠ABC交DC于点E . 若 ,则∠DEB的大小为( )
A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在 中,BE平分∠ABC交DC于点E . 若 ,则∠DEB的大小为( )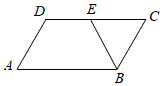 A、130° B、125° C、120° D、115°7. 下列各图是的函数的是( )A、
A、130° B、125° C、120° D、115°7. 下列各图是的函数的是( )A、 B、
B、 C、
C、 D、
D、 8. 一次函数其中 , 的图象大致为( )A、
8. 一次函数其中 , 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 9. 下列命题是假命题的为( )A、对角线相等的菱形是正方形 B、对角线互相垂直的矩形是正方形 C、对角线互相垂直且相等的平行四边形是正方形 D、对角线互相垂直且平分的四边形是正方形10. 如图,四边形是菱形, , , 于点 , 则的长为( )
9. 下列命题是假命题的为( )A、对角线相等的菱形是正方形 B、对角线互相垂直的矩形是正方形 C、对角线互相垂直且相等的平行四边形是正方形 D、对角线互相垂直且平分的四边形是正方形10. 如图,四边形是菱形, , , 于点 , 则的长为( ) A、 B、 C、 D、11. 如图,为等腰直角三角形, , 以斜边为直角边作等腰直角三角形 , 再以为直角边作等腰直角三角形 , , 按此规律作下去,则的长度为( )
A、 B、 C、 D、11. 如图,为等腰直角三角形, , 以斜边为直角边作等腰直角三角形 , 再以为直角边作等腰直角三角形 , , 按此规律作下去,则的长度为( ) A、 B、 C、 D、12. 如图,正方形的边长为 , 点在对角线上,且 , , 垂足为 , 则的长为( )
A、 B、 C、 D、12. 如图,正方形的边长为 , 点在对角线上,且 , , 垂足为 , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共8.0分)
-
13. 若最简二次根式能与合并,则的值为 .14. 在同一平面直角坐标系中,直线与相交于点 , 则关于 , 的方程组的解为 .15. 命题“有三个角是直角的四边形是矩形”的逆命题是: .16. 在中, , 为边上的高, , , 则的长为 .
三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
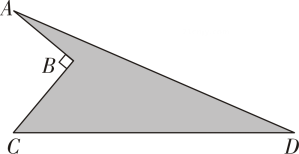
17. 计算:(1)、;(2)、 .18. 为深入学习贯彻党的二十大精神,贯彻落实习近平总书记关于教育的重要论述和重要指示批示精神,迪庆州某中学计划在如图阴影区域展示学生的学习心得现测得 , , , , 试求阴影部分的面积.
 19. 为了加强心理健康教育,某校组织八年级两班学生进行了心理健康常识测试,已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
19. 为了加强心理健康教育,某校组织八年级两班学生进行了心理健康常识测试,已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.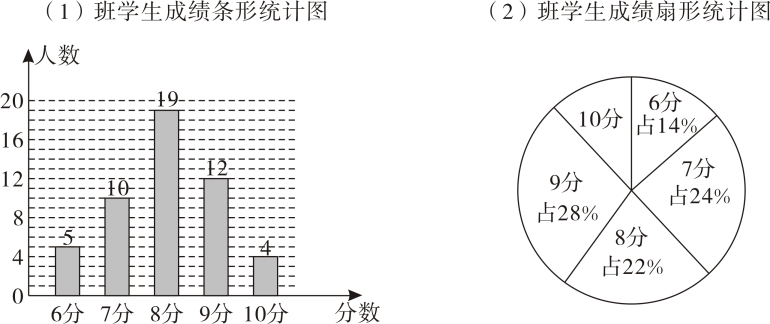 (1)、请确定下表中 , , 的值:
(1)、请确定下表中 , , 的值:统计量
平均数
众数
中位数
班
班
分, 分, 分;
(2)、根据上表中各种统计量,说明哪个班的成绩更突出一些.20. 如图,在四边形中,AB//DC, , 对角线 , 交于点 , 平分 , 过点作交的延长线于点 , 连接 .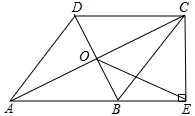 (1)、求证:四边形是菱形;(2)、若 , , 求的长.21. 一个有进水管与出水管的容器,从某时刻开始分钟内只进水不出水在随后的分钟内既进水又出水,直到容器内的水量达到如图,坐标系中两条线段和表示这一过程中容器内的水量单位:与时间单位:分之间的关系.
(1)、求证:四边形是菱形;(2)、若 , , 求的长.21. 一个有进水管与出水管的容器,从某时刻开始分钟内只进水不出水在随后的分钟内既进水又出水,直到容器内的水量达到如图,坐标系中两条线段和表示这一过程中容器内的水量单位:与时间单位:分之间的关系. (1)、单独开进水管,每分钟可进水 ;(2)、求进水管与出水管同时打开时容器内的水量与时间的函数关系式 .22. 如图,将矩形沿直线折叠,顶点恰好落在边上点处,已知 , , 求图中阴影部分的面积.
(1)、单独开进水管,每分钟可进水 ;(2)、求进水管与出水管同时打开时容器内的水量与时间的函数关系式 .22. 如图,将矩形沿直线折叠,顶点恰好落在边上点处,已知 , , 求图中阴影部分的面积. 23. “每天一杯纯牛奶”已经成为人们生活的健康时尚,市场上对牛奶的需求越发增大某乳品公司每月均需通过“飞快”快递公司向地输送一批牛奶“飞快”公司给出三种运费方案,具体如下:
23. “每天一杯纯牛奶”已经成为人们生活的健康时尚,市场上对牛奶的需求越发增大某乳品公司每月均需通过“飞快”快递公司向地输送一批牛奶“飞快”公司给出三种运费方案,具体如下:方案一:每千克运费元,按实际运输重量结算;
方案二:每月收取元管理费用,再每千克运费元;
方案三:每月收取元包干,不限运输重量.
设该公司每月运输牛奶千克,选择方案一时,运费为元,选择方案二时,运费为元,选择方案三时,运费为元
 (1)、请直接写出 , , 与之间的关系式;(2)、在同一个坐标系中,若三种方案对应的函数图象如图所示,请求出点 , , 的坐标,并直接写出如何选择方案更合算.24. 如图,在平面直角坐标系中,已知一次函数的图象与轴,轴分别交于 , 两点,以为边在第二象限内作正方形 .
(1)、请直接写出 , , 与之间的关系式;(2)、在同一个坐标系中,若三种方案对应的函数图象如图所示,请求出点 , , 的坐标,并直接写出如何选择方案更合算.24. 如图,在平面直角坐标系中,已知一次函数的图象与轴,轴分别交于 , 两点,以为边在第二象限内作正方形 .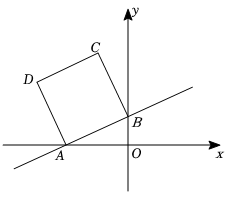 (1)、求正方形的面积;(2)、求点和点的坐标;(3)、在轴上是否存在点 , 使的周长最小?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、求正方形的面积;(2)、求点和点的坐标;(3)、在轴上是否存在点 , 使的周长最小?若存在,请求出点的坐标;若不存在,请说明理由.