云南省临沧市耿马县2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 以下列各组数作为三角形的三边长,能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,2. 下列根式中,是最简二次根式的是( )A、 B、 C、 D、3. 如图,四边形是平行四边形,以下四个结论中:
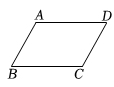
;;; .
正确的有( )
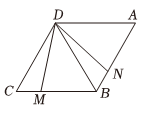
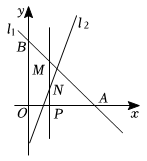
A、 B、 C、 D、4. 函数、为常数的图象如图所示,则不等式的解集是( )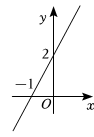 A、 B、 C、 D、5. 在中,点、、分别是三边的中点,若的周长为 , 则周长为( )A、 B、 C、 D、6. 某中学八年级有名同学参加了“走进古典数学,趣谈数学史话”的数学史知识竞赛,他们的初赛成绩各不相同,要取前名同学参加决赛,其中小智同学已经知道了自己的初赛成绩,他想知道自己能否进入决赛,还需要知道这名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,在中, , , , 是的垂直平分线,交于点 , 交于点 , 连接 , 则的长为( )
A、 B、 C、 D、5. 在中,点、、分别是三边的中点,若的周长为 , 则周长为( )A、 B、 C、 D、6. 某中学八年级有名同学参加了“走进古典数学,趣谈数学史话”的数学史知识竞赛,他们的初赛成绩各不相同,要取前名同学参加决赛,其中小智同学已经知道了自己的初赛成绩,他想知道自己能否进入决赛,还需要知道这名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,在中, , , , 是的垂直平分线,交于点 , 交于点 , 连接 , 则的长为( )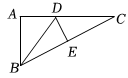 A、 B、 C、 D、9. 甲、乙、丙三名同学本学期四次月考的数学平均分都相同,方差分别是 , , , 由此可知,这三人成绩相对稳定的是( )A、甲 B、乙 C、丙 D、无法确定10. 按一定规律排列的单项式: , , , , , 第个单项式为( )A、 B、 C、 D、11. 如图,在正方形中,为上一点,连接 , 交对角线于点 , 连接 , 若 , 则的度数为( )
A、 B、 C、 D、9. 甲、乙、丙三名同学本学期四次月考的数学平均分都相同,方差分别是 , , , 由此可知,这三人成绩相对稳定的是( )A、甲 B、乙 C、丙 D、无法确定10. 按一定规律排列的单项式: , , , , , 第个单项式为( )A、 B、 C、 D、11. 如图,在正方形中,为上一点,连接 , 交对角线于点 , 连接 , 若 , 则的度数为( )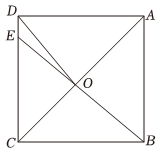 A、 B、 C、 D、12. 如图 , 在中, , 点从点出发,以每秒个单位长度的速度沿匀速运动到点 , 图是点运动时,线段的长度随时间变化的图象,则的边长为( )
A、 B、 C、 D、12. 如图 , 在中, , 点从点出发,以每秒个单位长度的速度沿匀速运动到点 , 图是点运动时,线段的长度随时间变化的图象,则的边长为( )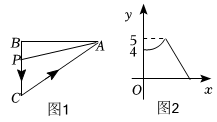 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共8.0分)
-
13. 式子有意义,则x的取值范围是 .14. 在中, , , 若点为的中点,则的度数为 .15. 将一次函数的图象先向左平移个单位长度,再向下平移个单位长度后得到的函数解析式为 .16. 矩形的对角线、相交于点 , , , 作 , , 、相交于点 , 则四边形的面积为 .
三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 如图,为使垂直于地面的建筑物不发生倾斜,工程师从该建筑物顶部的点向两边各引出两条钢缆和 , 分别固定在地面上的点和点已知钢缆长米,、两点到建筑物底部点的距离分别为米和米,求钢缆的长.
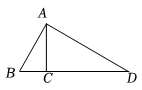 19. 已知 , , 求的值.20. 某公司销售部门全体职工的月工资单位:元如下:
19. 已知 , , 求的值.20. 某公司销售部门全体职工的月工资单位:元如下:;;;;;;:;: .
(1)、求该部门全体职工月工资的平均数、中位数和众数.(2)、第题中所求的个统计量,哪一个更能反映该部门的月工资水平?请说明理由.(3)、由于公司效益较好,该部门全体职工月工资均上涨元,则该部门职工月工资的“平均数、中位数、众数和方差”中,哪个统计量的大小没有发生变化?21. 如图,在中, , , 点在边上运动不与、两点重合 , , . (1)、求证:四边形是矩形.(2)、连接 , 当线段最短时, , 求此时的值.22. 为全面推进乡村振兴,某省实行城市援助乡镇的政策.该省的A市有120吨物资,B市有130吨物资.经过调研发现该省的甲乡需要140吨物资,乙乡需要110吨物资.于是决定由A、B两市负责援助甲、乙两乡、已知从A市往甲、乙两乡运送物资的运费分别为300元/吨、150元/吨,从B市往甲、乙两乡运送物资的运费分别为200元/吨、100元/吨.(1)、设从A市往甲乡运送x吨物资,从A、B两市向甲、乙两乡运送物资的总运费为y元,求y与x的函数解析式.(2)、请设计运费最低的运送方案,并求出最低运费.
(1)、求证:四边形是矩形.(2)、连接 , 当线段最短时, , 求此时的值.22. 为全面推进乡村振兴,某省实行城市援助乡镇的政策.该省的A市有120吨物资,B市有130吨物资.经过调研发现该省的甲乡需要140吨物资,乙乡需要110吨物资.于是决定由A、B两市负责援助甲、乙两乡、已知从A市往甲、乙两乡运送物资的运费分别为300元/吨、150元/吨,从B市往甲、乙两乡运送物资的运费分别为200元/吨、100元/吨.(1)、设从A市往甲乡运送x吨物资,从A、B两市向甲、乙两乡运送物资的总运费为y元,求y与x的函数解析式.(2)、请设计运费最低的运送方案,并求出最低运费.