云南省昆明市西山区2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下面计算正确的是( )A、 B、 C、 D、3. 一次函数的图象是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列条件中,能够判断为直角三角形的是( )A、 B、:::: C、 , , D、::::5. 少年强,则国强,为增强青少年科技创新能力,我市举行了“青少年机器人大赛”,经过一轮初赛后,共有人进入决赛他们决赛的成绩各不相同 , 本次活动将按照决赛分数评出一等奖名,二等奖名,三等奖名,小丽进入了决赛,要判断自己能否获奖,她应该关注决赛分数的( )A、平均数 B、方差 C、众数 D、中位数6. 顺次连结矩形各边的中点所得的四边形是( )A、正方形 B、菱形 C、矩形 D、平行四边形7. 如表记录了甲、乙、丙、丁四名同学参加某区“十九届六中全会”为主题的演讲比赛的相关数据:根据表中数据,从平均成绩优秀且成绩稳定的角度,选择甲同学参加市级比赛,则可以判断、的值可能是( )
4. 下列条件中,能够判断为直角三角形的是( )A、 B、:::: C、 , , D、::::5. 少年强,则国强,为增强青少年科技创新能力,我市举行了“青少年机器人大赛”,经过一轮初赛后,共有人进入决赛他们决赛的成绩各不相同 , 本次活动将按照决赛分数评出一等奖名,二等奖名,三等奖名,小丽进入了决赛,要判断自己能否获奖,她应该关注决赛分数的( )A、平均数 B、方差 C、众数 D、中位数6. 顺次连结矩形各边的中点所得的四边形是( )A、正方形 B、菱形 C、矩形 D、平行四边形7. 如表记录了甲、乙、丙、丁四名同学参加某区“十九届六中全会”为主题的演讲比赛的相关数据:根据表中数据,从平均成绩优秀且成绩稳定的角度,选择甲同学参加市级比赛,则可以判断、的值可能是( )甲
乙
丙
丁
平均数分
方差
A、 , B、 , C、 , D、 ,8. 如图,直线和直线相交于点 , 则方程组的解是( ) A、 B、 C、 D、9. 取一张边长为的正方形纸片,按如图所示的方法折叠两次,则线段的长为( )
A、 B、 C、 D、9. 取一张边长为的正方形纸片,按如图所示的方法折叠两次,则线段的长为( ) A、 B、 C、 D、10. 数学老师要求学生用一张长方形的纸片折出一个的角,甲、乙两人的折法如下,下列说法正确的是( )
A、 B、 C、 D、10. 数学老师要求学生用一张长方形的纸片折出一个的角,甲、乙两人的折法如下,下列说法正确的是( )甲:如图 , 将纸片沿折痕折
叠,使点落在上的点处,
即为所求,

乙:如图 , 将纸片沿折痕 ,
折叠,使 , 两点分别落在
点 , 处,与在同一
直线上,即为所求,
A、只有甲的折法正确 B、甲和乙的折法都正确 C、只有乙的折法正确 D、甲和乙的折法都不正确11. 如图,在中,、分别为、的中点,点在上,且 , 若 , , 则的长为( ) A、 B、 C、 D、12. 如图是由相同的菱形按一定规律摆放而成,第个图形有个菱形,第个图形有个菱形,第个图形有个菱形,按此规律排列下去,第个图形的菱形个数为( )
A、 B、 C、 D、12. 如图是由相同的菱形按一定规律摆放而成,第个图形有个菱形,第个图形有个菱形,第个图形有个菱形,按此规律排列下去,第个图形的菱形个数为( )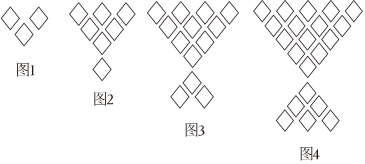 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共8.0分)
-
13. 在“永远跟党走,奋斗新征程“西山区青少年爱国主义教育演讲比赛活动中,已知某位选手的演讲内容、语言表达、形象风度这三项得分分别为分,分,分,若依次按照 , , 的百分比确定成绩,则该选手的成绩是 分14. 二次根式有意义的条件是 .15. 已知点、都在一次函数的图象上,比较大小: .16. 如图,在菱形ABCD中,AB=4,按以下步骤作图:①分别以点C和点D为圆心,大于 CD的长为半径画弧,两弧交于点M,N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,则BE的值为 .

三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算:(1)、;(2)、 .18. 阅读:在平面直角坐标系中,已知两点的坐标,可构造直角三角形,运用勾股定理,求这两点间的距离;在平面直角坐标系中有两点 , , 求 , 两点间的距离过点作轴的垂线,过点作轴的垂线,相交于点 , 连接 , , 在中,由勾股定理得: , 若 , , 从而得到两点间的距离公式解决下列问题:
 (1)、若 , , 则两点间的距离 ;(2)、如图:点 , 点 , 则 ,若 , 则 .19. 为了解西山区八年级学生数学学科期末质量监测情况,某数学兴趣小组进行了抽样调查,过程如下,请将有关问题补充完整:
(1)、若 , , 则两点间的距离 ;(2)、如图:点 , 点 , 则 ,若 , 则 .19. 为了解西山区八年级学生数学学科期末质量监测情况,某数学兴趣小组进行了抽样调查,过程如下,请将有关问题补充完整:收集数据:随机抽取甲、乙两所学校的名学生的数学成绩进行分析.
甲:
乙:
整理、描述数据:按如下数据段整理、描述这两组数据.
学校
甲
乙
分析数据:两组数据的平均数、中位数、众数、方差如表:
学校统计量
平均数
中位数
众数
方差
甲
乙
根据以上信息回答下列问题:
(1)、填表:的值是 ;的值是 ;(2)、得出结论:若甲学校有名八年级学生,请估计这次考试成绩在分及以上的人数;
请推断哪所学校学生的数学水平较高,并说明理由.
20. 生态体验园推出了甲、乙两种消费卡,设入园次数为时所需费用为元,选择这两种卡消费时,与的函数关系如图所示,解答下列问题: (1)、分别求出选择这两种卡消费时,关于的函数表达式;(2)、当入园次数在次含和 , 选择哪种卡消费方式比较合算?21. 如图,在 中,过点 作 于点 ,点 在边 上, ,连接 , .
(1)、分别求出选择这两种卡消费时,关于的函数表达式;(2)、当入园次数在次含和 , 选择哪种卡消费方式比较合算?21. 如图,在 中,过点 作 于点 ,点 在边 上, ,连接 , . (1)、求证:四边形 是矩形;(2)、已知 , 是 的平分线,若 ,求 的长度.22. 如图,直线:与过点的直线交于点 , 与轴交于点 .
(1)、求证:四边形 是矩形;(2)、已知 , 是 的平分线,若 ,求 的长度.22. 如图,直线:与过点的直线交于点 , 与轴交于点 . (1)、求直线的解析式;(2)、点在直线上,轴,交直线于点 , 若 , 求点的坐标.23. 冰墩墩(Bing Dwen Dwen)、雪容融(Shuey Rhon Rhon)分别是2022年北京冬奥会、冬残奥会的吉祥物.冬奥会来临之际,冰墩墩、雪容融玩偶畅销全国.小雅在某网店选中两种玩偶,决定从该网店进货并销售,第一次小雅用1400元购进了冰墩墩玩偶15个和雪容融玩偶5个,已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元,销售时每个冰墩墩玩偶可获利28元,每个雪容融玩偶可获利20元.
(1)、求直线的解析式;(2)、点在直线上,轴,交直线于点 , 若 , 求点的坐标.23. 冰墩墩(Bing Dwen Dwen)、雪容融(Shuey Rhon Rhon)分别是2022年北京冬奥会、冬残奥会的吉祥物.冬奥会来临之际,冰墩墩、雪容融玩偶畅销全国.小雅在某网店选中两种玩偶,决定从该网店进货并销售,第一次小雅用1400元购进了冰墩墩玩偶15个和雪容融玩偶5个,已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元,销售时每个冰墩墩玩偶可获利28元,每个雪容融玩偶可获利20元. (1)、求两种玩偶的进货价分别是多少?(2)、第二次小雅进货时,网店规定冰墩墩玩偶进货数量不得超过雪容融玩偶进货数量的1.5倍.小雅计划购进两种玩偶共40个,应如何设计进货方案才能获得最大利润,最大利润是多少元?24. 如图 , 直角梯形中, , , , , 点从点出发,以每秒个单位长度的速度向点运动,同时,点从点出发,以每秒个单位长度的速度向点运动其中一个动点到达终点时,另一个动点也随之停止运动过点作于点 , 连接交于点 , 连接设运动时间为秒.
(1)、求两种玩偶的进货价分别是多少?(2)、第二次小雅进货时,网店规定冰墩墩玩偶进货数量不得超过雪容融玩偶进货数量的1.5倍.小雅计划购进两种玩偶共40个,应如何设计进货方案才能获得最大利润,最大利润是多少元?24. 如图 , 直角梯形中, , , , , 点从点出发,以每秒个单位长度的速度向点运动,同时,点从点出发,以每秒个单位长度的速度向点运动其中一个动点到达终点时,另一个动点也随之停止运动过点作于点 , 连接交于点 , 连接设运动时间为秒. (1)、 , 用含的代数式表示(2)、当四边形为平行四边形时,求的值.(3)、如图 , 将沿翻折,得 , 是否存在某时刻 , 使四边形为菱形,若存在,求出的值;若不存在,请说明理由.
(1)、 , 用含的代数式表示(2)、当四边形为平行四边形时,求的值.(3)、如图 , 将沿翻折,得 , 是否存在某时刻 , 使四边形为菱形,若存在,求出的值;若不存在,请说明理由.