云南省曲靖市2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-09-19 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图是嘉淇不完整的推理过程.

 A、 B、 C、 D、4. 化简的结果是( )A、 B、 C、 D、5. 已知函数( , 为常数)的函数值随值的增大而减小,那么这个函数图象可能经过的点是( )A、 B、 C、 D、6. 有一列数按一定规律排列: , , , , , , 则第个数是( )A、 B、 C、 D、7. 在平面直角坐标系中,将直线沿轴向下平移个单位后,得到一条新的直线,该直线与轴的交点坐标是( )A、 B、 C、 D、8. 如图,以原点为圆心,长为半径画弧与数轴交于点 , 若点表示的数为 , 则的值为( )
A、 B、 C、 D、4. 化简的结果是( )A、 B、 C、 D、5. 已知函数( , 为常数)的函数值随值的增大而减小,那么这个函数图象可能经过的点是( )A、 B、 C、 D、6. 有一列数按一定规律排列: , , , , , , 则第个数是( )A、 B、 C、 D、7. 在平面直角坐标系中,将直线沿轴向下平移个单位后,得到一条新的直线,该直线与轴的交点坐标是( )A、 B、 C、 D、8. 如图,以原点为圆心,长为半径画弧与数轴交于点 , 若点表示的数为 , 则的值为( ) A、 B、 C、 D、9. 如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点.若 , , 则MN的长为( )
A、 B、 C、 D、9. 如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC的中点.若 , , 则MN的长为( ) A、 B、5 C、 D、410. 如图,已知函数 和 的图象交于点 ,则根据图象可得不等式 的解集是( )
A、 B、5 C、 D、410. 如图,已知函数 和 的图象交于点 ,则根据图象可得不等式 的解集是( )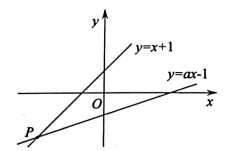 A、 B、 C、 D、11. 如图,菱形的对角线 , 相交于点 , 过点作于点 , 连接若 , 菱形的面积为 , 则的长为( )
A、 B、 C、 D、11. 如图,菱形的对角线 , 相交于点 , 过点作于点 , 连接若 , 菱形的面积为 , 则的长为( ) A、 B、 C、 D、12. “赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 , 较短直角边长为 , 若 , 大正方形的面积为 , 则小正方形的面积为( )
A、 B、 C、 D、12. “赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 , 较短直角边长为 , 若 , 大正方形的面积为 , 则小正方形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共8.0分)
-
13. 若式子 有意义,则x的取值范围是.14. 在一次舞蹈比赛中,甲、乙、丙、丁四队演员的人数相同,身高的平均数均为 , 且方差分别为 , , , 则这四队演员的身高最整齐的是队。15. 如图,在中, , , , 将折叠,使点与点重合,得折痕 , 则的周长等于 .
 16. 已知直线 , 该直线与两坐标轴围成的三角形面积为 , 那么的值是 .
16. 已知直线 , 该直线与两坐标轴围成的三角形面积为 , 那么的值是 .三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 计算: .18. 先化简,再求值 ,其中 .19. 如图,在四边形中, , 对角线平分 , 是上一点,过点作 , , 垂足分别为、 .
 (1)、求证:;(2)、若 ▲ 时,四边形是正方形,并说明理由.20. 光明学校为了提高学生的“甲流病毒防范”意识,特组织了一场“防疫”知识竞赛,学校在八、九年级中分别随机抽取了名学生的成绩分数进行整理分析,已知成绩分数均为整数,且分为 , , , , 五个等级,分别是:
(1)、求证:;(2)、若 ▲ 时,四边形是正方形,并说明理由.20. 光明学校为了提高学生的“甲流病毒防范”意识,特组织了一场“防疫”知识竞赛,学校在八、九年级中分别随机抽取了名学生的成绩分数进行整理分析,已知成绩分数均为整数,且分为 , , , , 五个等级,分别是:: , : , : , : , :并给出了部分信息:
八年级等级中由低到高的个分数为: , , , , , , , , , ;
两个年级学生“防疫”知识竞赛分数统计图:

两个年级学生“防疫”知识竞赛分数样本数据的平均数、中位数、众数如下:
平均数
中位数
众数
八年级
九年级
(1)、直接写出 , 的值;(2)、若分数不低于分表示该生对“防疫”知识掌握较好,该校八年级有学生人,九年级有学生人,请估计该校八、九年级所有学生中,对“防疫”知识掌握较好的学生人数.21. 如图,中,的垂直平分线分别交、于点、 , 且 . (1)、求证:;(2)、若 , :: , 求的长.22. 某商场销售甲、乙两种品牌的书包,已知该商场销售个甲品牌书包和个乙品牌书包的利润为元;销售个甲品牌书包和个乙品牌书包的利润为元.(1)、求每个甲品牌书包和每个乙品牌书包的销售利润;(2)、该商场购进甲、乙两种品牌的书包共个,其中乙品牌书包的进货量不超过甲品牌书包数量的倍,设购进甲品牌书包个,本次购进的个书包全部出售的销售总利润为元.
(1)、求证:;(2)、若 , :: , 求的长.22. 某商场销售甲、乙两种品牌的书包,已知该商场销售个甲品牌书包和个乙品牌书包的利润为元;销售个甲品牌书包和个乙品牌书包的利润为元.(1)、求每个甲品牌书包和每个乙品牌书包的销售利润;(2)、该商场购进甲、乙两种品牌的书包共个,其中乙品牌书包的进货量不超过甲品牌书包数量的倍,设购进甲品牌书包个,本次购进的个书包全部出售的销售总利润为元.求关于的函数关系式;
该商场如何采购,才能使销售总利润最大?最大利润是多少?

